離散型隨機(jī)變量數(shù)學(xué)期望的教學(xué)設(shè)計(jì)與實(shí)踐

滕興虎，趙穎，陳桂東，寇冰煜

（解放軍理工大學(xué) 理學(xué)院，江蘇 南京 211101）

離散型隨機(jī)變量數(shù)學(xué)期望的教學(xué)設(shè)計(jì)與實(shí)踐

滕興虎，趙穎，陳桂東，寇冰煜

（解放軍理工大學(xué) 理學(xué)院，江蘇 南京 211101）

教學(xué)實(shí)踐中，根據(jù)真實(shí)案例引入離散型隨機(jī)變量數(shù)學(xué)期望，通過對(duì)離散型數(shù)學(xué)期望概念的討論，促進(jìn)學(xué)生對(duì)數(shù)學(xué)期望內(nèi)涵的理解.改造傳統(tǒng)例題，利用數(shù)學(xué)軟件解決期望問題，有力的培養(yǎng)學(xué)生的建模意識(shí)、數(shù)學(xué)軟件應(yīng)用能力等綜合素質(zhì)，取得了較好的教學(xué)效果.

案例式教學(xué)；離散型隨機(jī)變量；數(shù)學(xué)期望；絕對(duì)收斂

數(shù)學(xué)期望是隨機(jī)變量的一個(gè)重要的數(shù)字特征，不但在概率論與數(shù)理統(tǒng)計(jì)的理論上占有重要地位，在實(shí)際生活中也有廣泛的應(yīng)用.因此，在授課時(shí)需要深入的剖析數(shù)學(xué)期望的內(nèi)涵，引導(dǎo)學(xué)生如何應(yīng)用期望理論解決問題.在通常的授課過程或教材中，往往是由簡(jiǎn)單的離散型隨機(jī)變量實(shí)例直接給出數(shù)學(xué)期望的定義.這樣的方式比較單調(diào)枯燥，容易造成學(xué)生對(duì)期望的理解是“形”上的，不夠深入.從多年的教學(xué)實(shí)踐發(fā)現(xiàn)，通過具體真實(shí)的案例出發(fā)，多次引導(dǎo)學(xué)生討論，能夠促使學(xué)生從討論中理解期望的內(nèi)涵.同時(shí)將教材中的例題進(jìn)行設(shè)計(jì)改造，也有助于培養(yǎng)學(xué)生的建模意識(shí)與綜合素質(zhì).實(shí)踐表明，這一教學(xué)方式取得較好的教學(xué)效果，有效、全方面地培養(yǎng)了學(xué)生的數(shù)學(xué)素養(yǎng).

1 引入真實(shí)案例，激發(fā)學(xué)習(xí)興趣

一般的，真實(shí)的案例比構(gòu)造的案例更具有吸引力.離散型隨機(jī)變量數(shù)學(xué)期望的教學(xué)，可以奧運(yùn)會(huì)中的真實(shí)情況作為切入點(diǎn).

馬修·埃蒙斯是一位美國(guó)射擊運(yùn)動(dòng)名將.埃蒙斯以成功的少年運(yùn)動(dòng)員身份起步，創(chuàng)下50 m運(yùn)動(dòng)步槍三姿射擊比賽少年世界紀(jì)錄，并在2002年和2004年國(guó)際射擊運(yùn)動(dòng)聯(lián)合會(huì)世界杯決賽中獲勝.在2002年ISSF冠軍賽和2004年雅典奧運(yùn)會(huì)射擊比賽中他獲得50 m運(yùn)動(dòng)步槍俯臥冠軍.然而2004年雅典奧運(yùn)會(huì)運(yùn)動(dòng)步槍三姿射擊比賽中，埃蒙斯的最后一槍脫靶，打了零環(huán)，將金牌拱手讓給了中國(guó)選手高占波.在為中國(guó)隊(duì)又添一枚金牌深感幸運(yùn)之余，引導(dǎo)學(xué)生思考：這次比賽成績(jī)是否是馬修·埃蒙斯的真實(shí)成績(jī)的體現(xiàn)，什么才是射擊天才馬修·埃蒙斯的真實(shí)水平.

奧運(yùn)史上這樣的事實(shí)，可以最大程度地激發(fā)學(xué)生的學(xué)習(xí)興趣，引發(fā)思考與討論.

2 推動(dòng)深入研討，得出準(zhǔn)確定義

2.1 分析案例，引出隨機(jī)變量取值有限時(shí)的數(shù)學(xué)期望

由式（1）可知，期望是隨機(jī)變量取值的一個(gè)加權(quán)平均，它是一個(gè)數(shù)值，不再是一個(gè)隨機(jī)變量.

2.2 深入探討，得到隨機(jī)變量取值可列無限時(shí)的數(shù)學(xué)期望

式（1）中對(duì)應(yīng)的是隨機(jī)變量取值有限時(shí)的數(shù)學(xué)期望.隨機(jī)變量的取值除了有限個(gè)，還可以取可列無限多個(gè).這時(shí)隨機(jī)變量的期望如何定義，是否只需要將式（1）中的n改為無窮即可，引發(fā)學(xué)生的再一次思考.

若將式（1）中的n改為無窮，則涉及到無窮級(jí)數(shù)，但無窮級(jí)數(shù)未必收斂.因此，要保證期望存在，至少需要加一個(gè)條件，即要求級(jí)數(shù)收斂.

此時(shí)，引發(fā)學(xué)生第3次思考，即僅有收斂性不能滿足期望的定義，應(yīng)該如何改進(jìn).

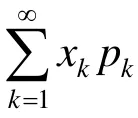
由定義2可知，隨機(jī)變量取值可列無限時(shí)，取值如果非負(fù)，則無需考慮絕對(duì)收斂性，否則，需要討論式（2）的絕對(duì)收斂性.

通過問題的逐層剖析，可促進(jìn)學(xué)生對(duì)離散型隨機(jī)變量數(shù)學(xué)期望概念的深入理解，進(jìn)而能夠在離散化的基礎(chǔ)上理解連續(xù)型隨機(jī)變量的數(shù)學(xué)期望.

3 轉(zhuǎn)化常見問題，培養(yǎng)建模意識(shí)

對(duì)于常見的隨機(jī)變量的數(shù)學(xué)期望，教材中往往是直接由分布求期望例題［2-4］.在具體授課時(shí)，可以根據(jù)需要進(jìn)行改造.

例1 某玩具店中每天賣出的某型玩具車的數(shù)量服從泊松分布，平均每天賣出2個(gè).試問他們每天應(yīng)準(zhǔn)備幾個(gè)此款玩具車才可保證以98%的可能性不缺貨.

此處售出的玩具車個(gè)數(shù)服從泊松分布，如果設(shè)每次賣出的個(gè)數(shù)為X，泊松分布的參數(shù)為λ，則X服從泊松p(λ).要確定準(zhǔn)備幾個(gè)才能保證以98%的可能性不缺貨，則需搞清楚分布情況.而要清楚分布情況，則需求出參數(shù)λ.問題轉(zhuǎn)化為求泊松p(λ)的期望E( X)，進(jìn)而由方程E( X)=2求出參數(shù)λ.

實(shí)踐表明，如此將文獻(xiàn)［2-4］中關(guān)于泊松分布期望的例題進(jìn)行改造轉(zhuǎn)化，可以有效地培養(yǎng)學(xué)生的建模意識(shí)，鍛煉學(xué)生分析問題和解決問題的數(shù)學(xué)能力.

4 運(yùn)用數(shù)學(xué)軟件，培養(yǎng)綜合素質(zhì)

數(shù)學(xué)期望的求解有多種方法［5-7］，在某些涉及大量隨機(jī)變量取值的數(shù)學(xué)期望時(shí)，可以采用數(shù)學(xué)軟件輔助求解，以節(jié)約時(shí)間，提高效率.

例2 體檢時(shí)為普查某種疾病，n個(gè)人需驗(yàn)血，現(xiàn)有如下驗(yàn)血方案：將k個(gè)人一組進(jìn)行分組，同組k個(gè)人的部分血樣混在一起化驗(yàn).

若結(jié)果為陰性，則說明k個(gè)人的血液都呈陰性，此k個(gè)人都無此疾病，這k個(gè)人只需化驗(yàn)1次；若混合血樣為陽性，則說明k個(gè)人中至少一人的血樣呈陽性反應(yīng)，應(yīng)對(duì)k個(gè)人的剩余血樣逐個(gè)化驗(yàn)，找出有病者，此時(shí)k個(gè)人的血需化驗(yàn)k+1次.設(shè)該疾病的帶病率為0.1，且得此病相互獨(dú)立.試問：（1）分組驗(yàn)血方案能否減少工作量；（2）如果能減少工作量，如何分組可以最大程度減少工作量.

在Maple2015數(shù)學(xué)軟件中運(yùn)行命令：

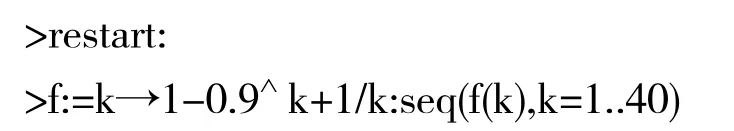
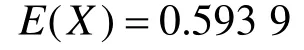
此外，還可以在Maple2015數(shù)學(xué)軟件中運(yùn)行命令：

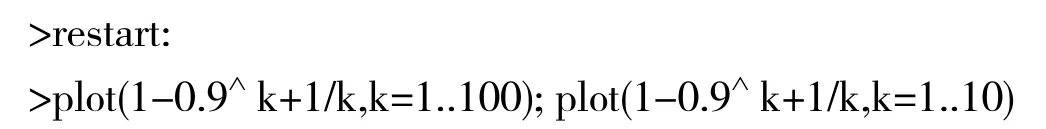
得到E( X)關(guān)于變量k的函數(shù)圖形（見圖1）.由圖1可以看出，當(dāng)0＜k＜10時(shí)，E( X)取得最小值，在k＞35時(shí)，，如此分組不但沒有減少工作量，反而增加了工作量.每組4人為最佳分組人數(shù).

圖1 E( X)關(guān)于k的函數(shù)圖形

根據(jù)期望的定義，結(jié)合數(shù)學(xué)軟件求解某些問題的期望，不但可以提高解決問題的效率，一定程度上也可以培養(yǎng)學(xué)生的綜合素質(zhì).

5 結(jié)語

在多年的教學(xué)實(shí)踐中，通過真正有趣的實(shí)例引入、抽絲剝繭的深入分析、恰當(dāng)合理的例題改造及適當(dāng)?shù)倪\(yùn)用數(shù)學(xué)軟件，一方面可以擺脫傳統(tǒng)教材與教學(xué)中單調(diào)、枯燥的教學(xué)方式，另一方面可以引起學(xué)生的高度興趣，培養(yǎng)學(xué)生的抽象能力、建模能力和軟件能力，全方位培養(yǎng)學(xué)生的綜合素質(zhì)，達(dá)到較好的教學(xué)效果.

［1］ 盛驟，謝式千，潘承毅.概率論與數(shù)理統(tǒng)計(jì)［M］.4版.北京：高等教育出版社，2008：90-100

［2］ 茆詩松，周紀(jì)薌.概率論與數(shù)理統(tǒng)計(jì)［M］.2版.北京：中國(guó)統(tǒng)計(jì)出版社，2000：48-94

［3］ 楊永發(fā).概率論與數(shù)理統(tǒng)計(jì)教程［M］.天津：南開大學(xué)出版社，2000：130-137

［4］ 王松桂，程維虎，高旅端.概率論與數(shù)理統(tǒng)計(jì)［M］.北京：科學(xué)出版社，2000：100-110

［5］ 唐秋晶，蔣傳鳳.數(shù)學(xué)期望的幾種求法［J］.洛陽師范學(xué)院學(xué)報(bào)，2000，19（5）：13-14

［6］ 肖文華.數(shù)學(xué)期望的計(jì)算方法與技巧［J］.湖南工業(yè)大學(xué)學(xué)報(bào)，2008，22（3）：98-100

［7］ 覃光蓮.數(shù)學(xué)期望的計(jì)算方法探討［J］.高等理科教育，2006，69（5）：41-45

Teaching design and practice of discrete random variable mathematics expectation

TENG Xing-hu，ZHAO Ying，CHEN Gui-dong，KOU Bing-yu
（Institute of Science，PLA University of Science and Technology，Nanjing 211101，China）

By introducing a true example，the concept of the discrete random variable mathematical expectation is discussed，and it help the students to understand the concept.By transforming a traditional example and solving a problem using mathematics software，the comprehensive qualities of student are developed powerfully.Also，better teaching effect is achieved in the teaching practice.

case teaching；discrete random variable；mathematical expectation；absolute convergence

O211.9∶G642.0

A

10.3969/j.issn.1007-9831.2016.06.022

1007-9831（2016）06-0071-04

2016-01-01

解放軍理工大學(xué)教學(xué)改革現(xiàn)實(shí)課題（JW1514）

滕興虎（1975-），男，江蘇邳州人，講師，碩士，從事數(shù)學(xué)教育與非線性動(dòng)力學(xué)研究.E-mail：liuqian@xidian.edu.cn