復雜多邊形快速融合算法與實現
楊 洋,劉學軍,肖 斐
(1. 61175部隊,江蘇 南京 210049;2. 南京師范大學,江蘇 南京 210046;3. 香港理工大學,香港 999077)
復雜多邊形快速融合算法與實現
楊 洋1,劉學軍2,肖 斐3
(1. 61175部隊,江蘇 南京 210049;2. 南京師范大學,江蘇 南京 210046;3. 香港理工大學,香港 999077)

空間矢量數據結構復雜且信息豐富,復雜多邊形作為矢量數據的重要組成部分,可由多個外環鏈和內環鏈組合而成,復雜的拓撲關系給相應算法的實現帶來了極大困難。多邊形快速融合作為GIS的基本功能,需要快速實現對任意、多個、復雜多邊形的融合處理。根據多邊形重心進行行列劃分,利用排斥實驗和多線程技術,實現了對任意多個復雜多邊形的快速合并。算法已在生產實踐中得到應用。
復雜多邊形;快速融合;多線程;排斥實驗
實現對任意多個復雜多邊形的快速融合對計算機輔助制圖、GIS矢量計算、計算機輔助設計等領域具有重要意義[1]。然而,現有軟件和算法在解決該問題上仍不夠全面,如傳統多邊形綜合方法主要基于柵格圖像,通過數學形態學方法來合并多邊形[2];大部分GIS軟件只實現了對簡單多邊形的兩兩合并,或多邊形合并必須滿足一定條件(如ArcGIS、MapGIS)。文獻[2]對多邊形進行CDT剖分,通過聚類實現對相接和相鄰多邊形的融合來實現自動制圖綜合,但算法效率和準確度不高,且未考慮屬性約束條件;文獻[3]、[4]只實現了對包含重復邊的左右多邊形的融合,復雜的拓撲構建和限定的適用條件使得算法普適性較差;文獻[5]只實現了對凸多邊形的融合,提出對凹多邊形的融合是將其分解為多個凸多邊形,但當多邊形極度破碎時僅分解凹多邊形就會帶來很大開銷,且沒有考慮更為復雜的情況;文獻[6]提出基于掃描線技術的合并算法,可解決非簡單多邊形和病態多邊形,但算法欠缺對內部多邊形的合并且回路頂點維護復雜。
據此,本文以帶有屬性特征的復雜多邊形作為研究對象,包括凹凸多邊形和含島嵌套多邊形,提出了基于復雜多邊形重心的網格劃分法,并結合排斥實驗、多線程處理來提高對多個復雜多邊形的處理速率,結合計算幾何[7]中的空間矢量求交算法實現了對任意相交或相接的復雜多邊形的快速融合,并已在實際生產中得到大量數據的驗證。
1 算法基礎
1.1 問題描述
復雜多邊形由多個互不相交且屬性相同的外環鏈和內環鏈組成。環鏈根據頂點序列方向的不同進行劃分:逆時針為外環鏈,順時針為內環鏈。復雜多邊形相互融合即各環鏈進行相交計算并重新組合的過程,融合過程中需要解決對頂點序列的維護、對點與環鏈空間關系的判斷、對多邊形進行拓撲重構等問題。
1.2 線段間求交
采用排斥實驗減少求交次數,通過跨立實驗準確判斷相交。如果兩條線段相交則必然相互跨立,則線段P1P2跨立Q1Q2(圖1)的依據為:
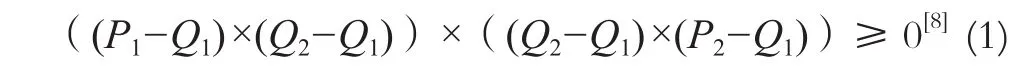
兩條線段相交分為8種情況(圖2):a中P1P2、Q1Q2交于A點;b中P1P2新增交點Q1;c中Q1Q2新增交點P2;d中P1P2新增交點Q1、Q2;e中Q1Q2新增交點P1、P2;f和h中無新增交點;g中P1P2新增交點Q1,Q1Q2新增交點。

圖1 快速排斥實驗與跨立實驗[8]

圖2 線段相交的8種情況
1.3 環鏈自相交檢測
環鏈自相交檢測的目的是維護環鏈幾何特征的一致性,是數據預處理的關鍵部分。當組成環鏈的線段除了頂點外還存在其他相交點則認為環鏈自相交(或稱病態多邊形[6]),處理過程為:
1)對組成環鏈的線段進行線段間求交,判斷是否存在新的相交點,若存在則向下執行(圖3a、圖4a、圖5a);不存在則停止處理。
2)按原線段方向對交點進行排序,并分割線段。
3)對分割后的線段集進行閉合環鏈搜索,生成新的環鏈集合(圖3b、圖4b、圖5b)。
4)若新生成環鏈面積小于閾值則舍去。
5)檢測環鏈間的包含關系:當環鏈相嵌套時,保留最外層的環鏈(圖3b舍去L2);當環鏈屬性相同但不嵌套時不進行處理(圖4b保留L1、L2、L3);剔除與原始環鏈屬性不同的新生成的環鏈(圖5b舍去L2、L4)。
1.4 點與環鏈位置關系的判斷

圖3 環鏈內部的自相交

圖4 相連情況下的環鏈自相交
點與任意形狀環鏈的關系可分為外部點、內部點、頂點和邊界點,圖6中描述了由頂點序列組成的外環鏈L與任意點Q的4種位置關系。鑒于射線法的缺陷[10],本文采用角度累加判別法[11],其原理為沿環鏈頂點順序求點Q與頂點構成的方向線的夾角(如QP1到QP2的角度θ1),以逆時針為正,順時針為負,范圍為最后得到角度的和當Q與P中任意一點相等時,Q為頂點;當Q位于L的某一條邊上時加權,Q為邊界點;當L為外環鏈,且ω=360°時,Q為內部點,否則Q為外部點;當L為內環鏈,且ω=-360°時,Q為外部點,否則Q為內部點。
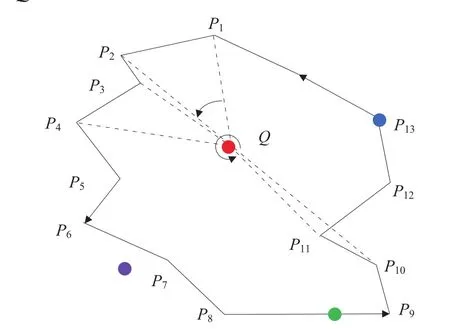
圖6 點與外環鏈的位置關系
1.5 環鏈間相交計算
復雜多邊形的融合可分解成環鏈間的兩兩融合,因此判斷環鏈間位置關系是關鍵。環鏈間位置關系的判斷建立在點與環鏈位置關系判斷的基礎上,通過環鏈最小包圍盒的排斥實驗可以排除一部分相離的環鏈,表1中列出了兩條環鏈可能的位置關系、判斷條件和融合結果。
1.6 多邊形間融合

表1 環鏈間位置關系的判斷
多邊形融合的步驟為:①對環鏈進行兩兩相交,新生成的相交點對原環鏈進行打斷(圖7a);②判斷環鏈A與環鏈B的位置關系,生成融合結果;③完成對兩個多邊形所有環鏈的融合;④對多邊形自身環鏈進行相交處理,消除重疊部分的環鏈;⑤通過正面積法來確定環鏈間包含關系[12],生成新的多邊形,圖7b為數據進行合并后的結果。
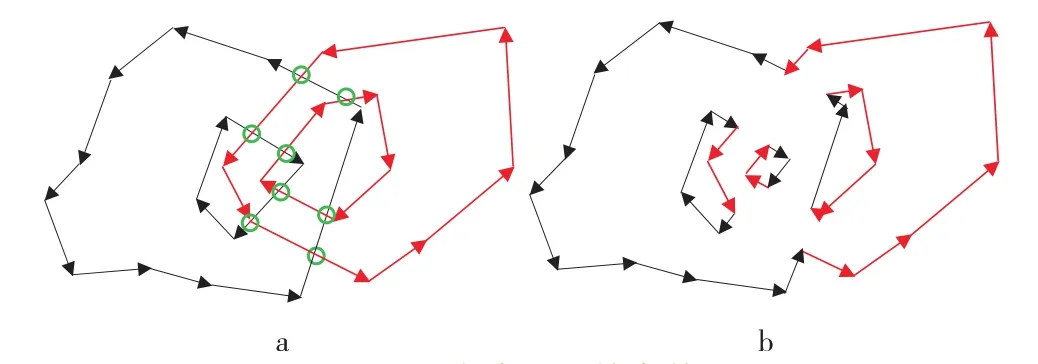
圖7 多個環鏈的合并
2 算法設計
2.1 算法流程
復雜多邊形的融合需要對輸入的初始多邊形進行預處理,如消除重復點、閉合環鏈、環鏈的自相交檢測等,將多邊形對象轉化為本算法所定義的數據結構,再進行多邊形的融合,具體流程如圖8所示。
2.2 數據結構
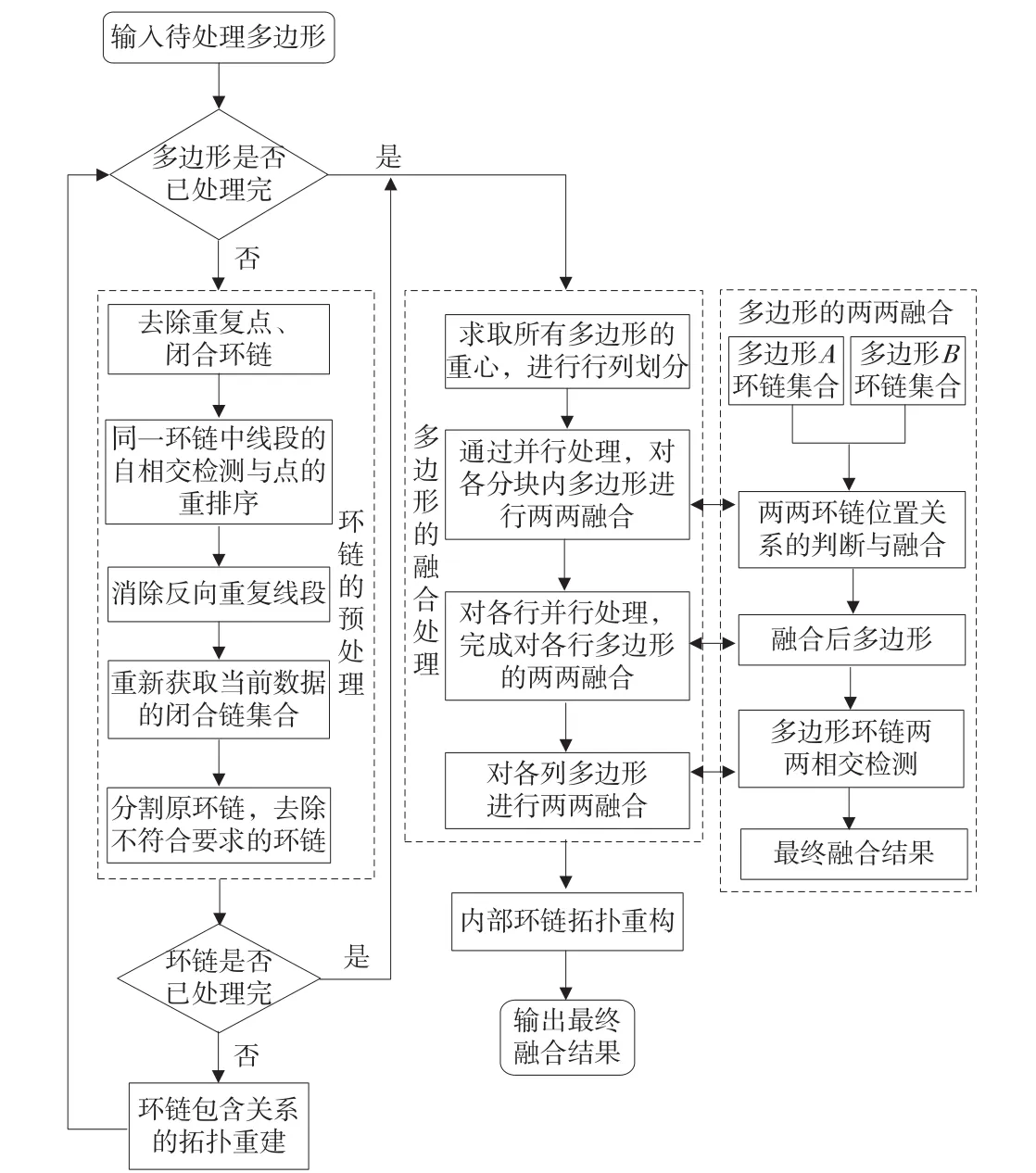
圖8 算法流程圖
描述復雜多邊形的數據結構包括點結構、線結構和環鏈結構,其數據結構定義如下:
//點結構
Class PointF{
Private:
float x, y;
}
//線結構
Class LineF{
Private:
PointF p1, p2;
float angle;
}
//環鏈結構
Class LinkAttri{
Private:
LinkStyle linkstyle; //內外屬性 值為OutLoop, InnerLoop
Vector bool crossed; //是否與其他鏈相交 PlyDirection plydirect; //環鏈的走向值為Deasil, AntiClockwise, Exceptional Corner4Points linkcorner4points; //環鏈包圍盒4 個角點坐標 LinkAttri(){ crossed = false; } }; //復雜多邊形結構 Class Polygon{ Private: int linknum; //環鏈個數 Map Corner4Points plycorner4points; //多邊形包圍盒4個角點坐標 Vector PointF geocenter; //多邊形的重心 } 2.3 基于重心的網格劃分 當所需處理的復雜多邊形數量多、結構復雜、分布散亂、破碎度高時,按存儲順序進行多邊形的兩兩融合會導致空間與時間開銷大、處理效率低。已有文獻中采用隊列[13]、建立四叉樹索引[1]等方法來加快數據的處理速度。鑒于復雜多邊形空間形態的多樣性,規則的四叉樹并不合適多邊形的劃分,本文將多邊形的幾何重心點作為劃分對象,計算公式為: 圖9 按多邊形的重心進行行列劃分 本算法的實驗平臺為Qt 5.3.0,待處理數據通過文本進行讀取。對比ArcGIS中的合并操作Dissolve和Eliminate,所處理的多邊形都非復雜多邊形,前者可將所選多邊形全部合并成一個,但丟失多邊形屬性,后者在合并中保留屬性,但不能一次合并很多,只能兩兩合并;而MapGIS中只能順次選擇合并2個相鄰區域,且多邊形也非復雜多邊形。本算法在考慮屬性的同時實現了對多個復雜多邊形的快速融合,普適性強。 1)多個簡單多邊形的融合。圖10a中不同顏色代表不同的多邊形,合并后生成的復雜多邊形由2個外環和2個內環構成,如圖10b所示。 圖10 簡單多邊形融合 圖11 多個復雜多邊形融合 本文對多邊形融合算法進行了全面擴展,通過基于重心的網格劃分,實現了對任意多個簡單多邊形、非簡單多邊形、復雜多邊形的快速融合處理,并通過數據預處理解決了環鏈自相交問題。對于多邊形拓撲結構的嚴格定義與維護,保證了其計算結果的正確性與穩定性。 [1] 唐立文,王榮峰,廖學軍.基于四叉樹的海量空間矢量多邊形處理技術[J].裝備指揮技術學院學報,2007,18(3):104-108 [2] 何宇兵.地學制圖綜合中多邊形對象的合并算法研究與應用[D].杭州:浙江大學,2007 [3] 郭仁忠,艾廷華.制圖綜合中建筑物多邊形的合并與化簡[J].武漢測繪科技大學學報,2000,25(1):25-30 [4] 馬麗娜.面向大規模空間數據的空間計算模式研究與實現[D].武漢:中國地質大學,2011 [5] 黃俊華,閆遂軍,朱小龍,等.一種凸多邊形的交、并求解算法[J].桂林工學院學報,2007,27(4):589-592 [6] 葉琳,邱龍輝.多邊形合并的算法研究[J].計算機應用與軟件,2002(8):57-59 [7] 周培德.計算幾何——算法設計與分析[M].北京:清華大學出版社,2011 [8] Schneider P J, Eberl Y D H.計算機圖形學集合工具算法詳解[M].北京:電子工業出版社,2005 [9] 鮑其勝,王慶,何立恒.基于線段操作的多邊形求交算法研究[J].測繪通報,2013(5):35-37 [10] 劉曉婧,趙俊三.判定點與多邊形及簡單多邊形之間的空間關系[J].科技情報開發與經濟,2008,18(28):223-224 [11] 鄒有建,肖龍鑫,陳鼎.判斷某點是否在任意多邊形內兩種算法的比較[J].地礦測繪,2009,25(3):28-30 [12] 彭認燦,陳子澎,劉國輝.快速確定多邊形與多邊形包含關系的一種新方法[J].測繪通報,2006(5):50-52 [13] 姚路,莫國明.地形圖房屋接邊合并算法與實現[J].城市勘測,2005(4):28-31 P208 B 1672-4623(2016)03-0052-04 10.3969/j.issn.1672-4623.2016.03.017 楊洋,碩士,主要研究方向為三維GIS、空間分析算法和地理空間情報。 2015-03-17。 項目來源:國家自然科學基金資助項目(41371421)。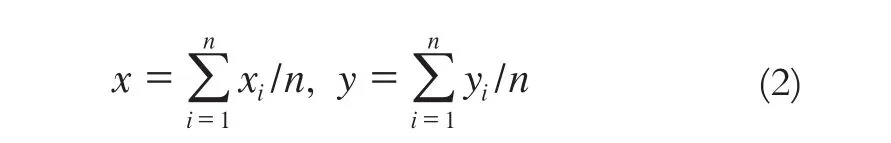

3 實驗分析


4 結 語

