船舶動力定位系統的加速度反饋控制

張 濤， 王 磊， 王洪超

(上海交通大學 海洋工程國家重點實驗室，高新船舶與深海開發裝備協同創新中心，上海 200030)

?

·實驗技術·

船舶動力定位系統的加速度反饋控制

張 濤， 王 磊， 王洪超

(上海交通大學 海洋工程國家重點實驗室，高新船舶與深海開發裝備協同創新中心，上海 200030)

以某一駁船為例，應用Fossen教授提出的狀態觀測器設計，在PID控制系統中加入加速度反饋項，選取兩個典型環境力方向角度60°和90°，分別設置不同的加速度增益值進行研究，比較加入加速度反饋項對定位能力的影響并討論選取最優增益值。通過數值模擬分析得出，90°時定位精度較差。在同一迎浪角度時，隨著增益值從0不斷增加，定位精度不斷提高；如果增益值一直增大，定位精度反而下降，選用適當的加速度反饋增益可以大大增加裝有動力定位的浮式結構物的定位能力。引入加速度反饋這一方法特別適合本身質量很小的結構物，對外干擾力的不那么敏感，從而提高動力定位精度。

無緣觀測器； PID控制； 加速度反饋； 數值模擬

0 引 言

近20多年來，隨著全球對石油和天然氣需求量的增加，世界海洋石油和天然氣勘探、生產穩步上升，同時也很大程度上促進了深海海洋工程的發展[1]。在近海或一般水深情況下，系泊定位是浮式生產系統的主要定位方式，但隨著水深的增加，一般的系泊定位方式顯示出了不足[2]。動力定位是具有不受海水深度和海況的影響、定位準確快速、操作方便等特點的一種定位方式，這使得海洋平臺和船舶在深水情況下精準定位成為可能[3]。

動力定位系統是一種閉環控制系統，它一般由位置測量系統、控制系統、推力系統組成。位置測量系統測量船舶位置;控制器根據測量船位與期望值的偏差，計算出抵抗環境干擾力(風、浪、流)使船舶恢復到期望位置所需的推力;推力系統進行各推力器推力的分配，推力器產生的推力使得船舶在外干擾力時仍能保持一定位置[4]。在環境力中的波浪力對浮式結構的作用一般可分為一階波浪力和二階波浪力，其中一階波浪力的激勵表現出來的是浮式結構的波頻震蕩;二階波浪力的激勵表現出來的是浮式結構的平均漂移和低頻振蕩，還有如TLP平臺(張力腿平臺)的張力腿與高頻激勵力發生共振產生高頻振蕩[5]。由于相對于低頻其波頻振蕩的頻率較高，通過推力器產生推力很難控制其運動，并且波頻振蕩位置變化可以自動回復，其表現出來的運動一般是垂直面的3自由度運動(橫搖(roll)、縱搖(pitch)、垂蕩(heave))，所以動力定位一般不抵抗高頻振蕩[6]。對于平均漂移和低頻振蕩需要抵抗，其運動表現出來的是水平面的3自由度運動(縱蕩(surge)、橫蕩(sway)、艏搖(yaw))。風力、海流力以及系泊力一般認為是低頻力。

動力定位系統中的測量系統所測得的船舶運動信號是6自由度相互耦合的，因此狀態觀測器就是對運動測量信號進行重建和預估，輸出低頻運動信號進入控制回路，完成整個定位控制過程。本文論述的加速度反饋的加速度項是從狀態觀測器中輸出，因此狀態觀測的好壞直接影響到動力定位系統控制的優劣與其定位精度。第一代船舶動力定位系統運用陷波濾波器和低通濾波器來濾除船舶運動的高頻信號，并由PID控制方法來補償船舶低頻運動，但相位延遲影響了動力定位精度[7]。第二代船舶動力定位系統將Kalman濾波理論與最優控制方法結合，增加了動力定位性能，但Kalman濾波器的缺點是對于協調一個由15個狀態和120個方差的隨機系統，即狀態估計器[8]是很困難的，也很費時，而且此方法也將船舶運動進行線性化處理，使其狀態估計值存在較大的誤差。本文針對Fossen教授團隊所設計的非線性無源觀測器[9]進行數值模擬并分析其濾波效果。

現代控制系統基于各種各樣的控制理論，其中包括PID控制、線性二次最優控制、隨機控制、模糊控制等，PID控制最早應用于動力定位系統中，由于其簡單、比較可靠的控制能力，PID控制策略得到了廣泛的應用[10]。本文基于PID經典控制理論，在控制方程中加入加速度反饋項，從理論出發并進行數值模擬分析，經比較得出適當的加速度增益可以有效地提高定位能力，尤其是針對自身慣性較小的浮式結構。

1 非線性無源觀測器數值模擬

1.1 偏誤模型的建模

海洋控制領域經常采用的偏誤模型為一階Markov過程[11]，

(1)

其中:b∈R3為緩變環境力和力矩的偏誤向量;n∈R3為均值為0的高斯白噪聲向量;T∈R3×3為對角線為正時間常數的對角矩陣;Ψ∈R3×3為n的縮放矩陣。上述模型可以用來描述包括二階波浪漂移力、流力、風力以及其他緩變動力。忽略白噪聲并對其進行拉普拉斯變換,可得：

(2)

1.2 一階運動模型

線性波頻模型[12]可以表示為：

(3)

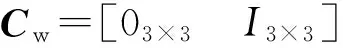
y=η+ηw

(4)

1.3 波浪譜近似

波浪譜近似公式為

(5)

其中:Kw=2λiω0iσ，ω0i(i=1～3)和λi為各自由度所對應的譜峰頻率和相對阻尼比，σi是與譜密度有關的參數。

上述的近似形式可以寫成狀態空間[13]的形式：

(6)

其中：

1.4 測量系統模型

對于一般船舶來說，只有位置和艏向可以通過GNSS(Global Navigation Satellite System)和電羅經得到，測量得到的位置和艏向可以表示為

y=η+ηw+d

(7)

其中:ηw代表波頻運動;d∈R3為零均高斯測量白噪聲向量。同時，控制系統還需要知道推力信息，推力可以表示為

τ=Buu

(8)

1.5 系統模型

為了建立系統模型[11]，進行了以下假設：

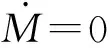
(2)n=w=0。觀測器模型在設計中忽略了偏誤模型和波頻模型的高斯白噪聲，因為此時觀測器可以通過估計誤差來進行驅動，不必由高斯白噪聲來進行驅動。

(3)d=0。相比于一階干擾ηw，零均測量白噪聲的影響可以忽略。

(4)R(η)=R(y)或者R(ψ)=R(ψ+ψw)，即假設并不考慮波頻運動引起的歐拉角變化導致的轉換矩陣的變化。實際情況中發現，在極端海況條件下一階波頻艏搖運動幅度一般小于5°；普通海況條件下，一階波頻艏搖運動幅度小于1°，所以這是一個非常好的假設。

建立在以上模型以及假設的基礎上，可以得到最終系統模型為：

(9)

為了表達簡便，可以把方程(a)～(c)合并，以狀態空間的形式進行表示：

(10)

其中:

從而系統方程變為如下形式：

(11)

1.6 觀測器方程[13]

(12)

將非線性無源觀測器用控制方塊圖表示，如圖1所示，從圖中可以看出，由羅經測量的位置信息與上一個過程狀態觀測器的估計值比較做差，作為驅動觀測器狀態估計變量，由波頻估計模塊估計出波頻運動，同時通過低頻估計模塊估計出低頻外力并運用運動方程求解得到低頻運動，之后將低頻運動和高頻運動進行疊加作為估測器的觀測估計值進行下一個循環。整個循環過程中，系統的其他狀態，如速度等也通過狀態觀測器得到了估計與重建。

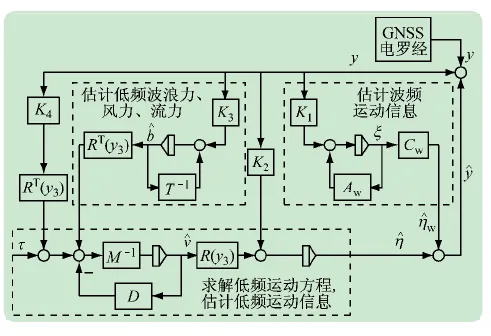
圖1 非線性狀態觀測器框圖

此觀測器增益值的設置比較困難，要滿足線性時不變(LTI)系統穩定性分析[14]的兩個等式，通常設有一定的調優規則能保證這兩個等式一定成立，則一般情況下有兩種方式來解決這一問題：①嘗試錯誤法，即選擇一系列的觀測器參數進行調試，檢驗是否滿足穩定性要求。由于沒有一定規則來選取增益值，所以調試工作可能會花費很長時間;②通過計算機高級算法解決穩定性約束問題來進行調優。

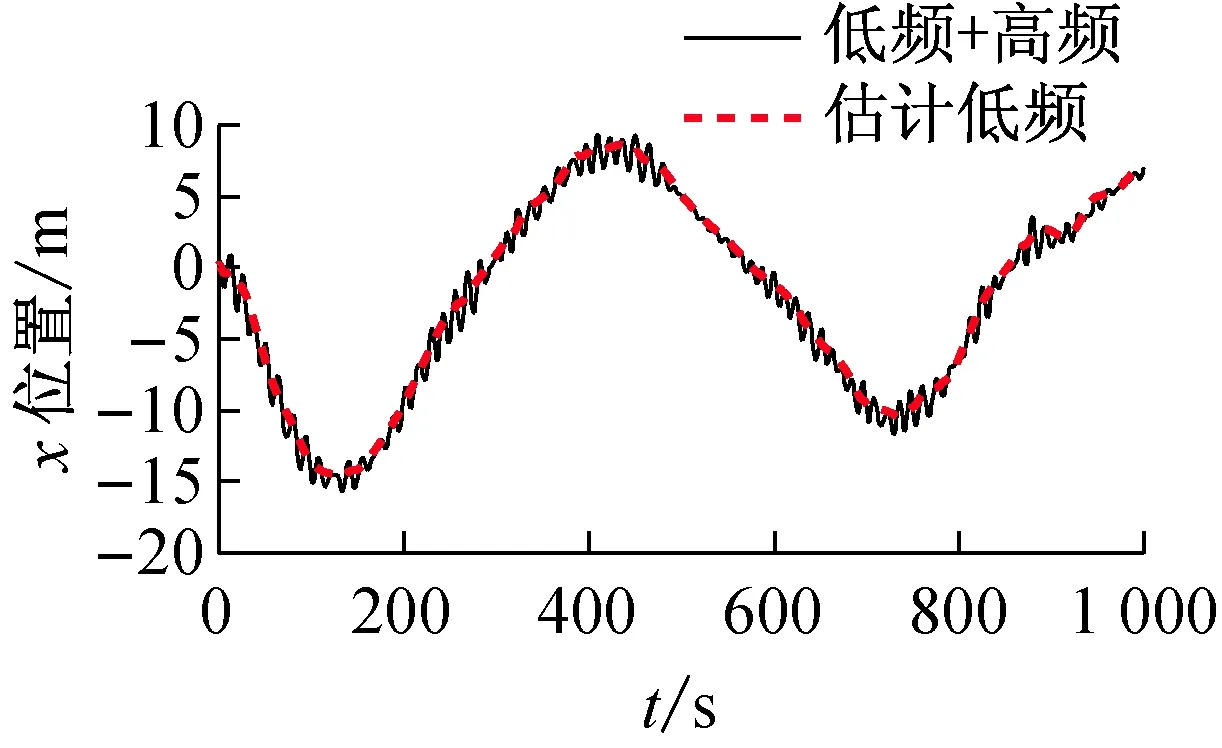
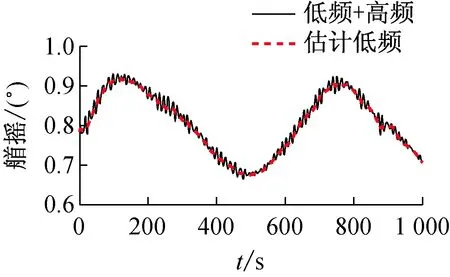
圖2 非線性狀態觀測器濾波在3自由度下濾波效果

利用上述已設計好的非線性狀態觀測器對測量運動位置信息進行濾波，其濾波效果如圖2所示。由圖可以看出，所設計的非線性狀態觀測器可以對低頻信號進行很好的估計與重建，沒有明顯的相位滯后現象。

2 加速度反饋控制

2.1 PID控制器

PID控制原理圖[11]如圖3所示，PID控制器由比例、積分、微分結合而成，是對偏差進行比例運算、積分運算和積分運算的線性組合，因此PID控制是一種線性控制算法。其傳遞函數可表示為:

(13)

把這3個環節各自的增益調整組合起來可以構成一種控制矯正器，所以在不知道控制系統的先驗信息的情況下仍然可以進行控制操作。

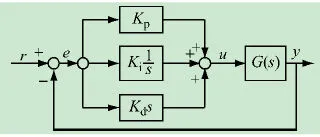
圖3 PID控制原理圖

2.2 加速度反饋

動力定位控制系統設計通常包括反饋控制和前饋控制。對于通常的PID控制，系統推力器輸出總推力為

(14)

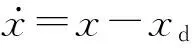
可以看出，控制系統利用位置和速度的反饋信息來計算推力輸出。考慮關于船舶動力定位模型的線性質量-剛度-阻尼系統：

(15)

當考慮加速度反饋的情況時，輸出推力τ可以表示為

(16)

其中:Km為加速度反饋增益;τPID為PID控制力。把式(16)代入式(15)，從而得到：

(17)

寫成標準形式有：

鄉村教師支持計劃背景下教師生存狀態省思——基于2888名鄉村教師的調查分析………………張曉文 張 旭(4·80)

(18)

由式(18)可以看出，增加了加速度反饋，相當于把船體的質量從m變成了m+Km，從而相當于將外界干擾的影響從ω減小到了ω/m+Km，使得系統對外界干擾變得沒有那么敏感。

假設在上述設計的控制方程中引入與頻率有關的虛擬質量hm(s)，如下式所示:

(19)

則可以通過低通濾波僅對低頻的加速度變化進行反應和抵抗，如取hm(s)為低通濾波器：

(20)

其中:增益Km和時間常數Tm均大于零，從而可以看到，系統變為

(21)

如令:

(22)

可以看出，當頻率很低，即s→0時，總質量為m+Km；當頻率很高，即s→∞時，總質量由m+Km減小到m。

從理論分析得出，加入虛擬質量相當于增加了結構物總質量，同時也是對外干擾力的一種耗散，使得系統對外環境力不那么敏感。加速度反饋與PID控制反饋聯合反饋控制流程框圖如圖4所示。

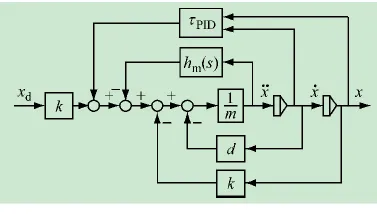
圖4 加速度反饋控制流程圖

以一裝有動力定位裝置的駁船為例，展示并驗證其傳統PID控制加上加速度反饋項對動力定位精度的優化改進作用。由于忽略了風力和流力，此次模擬的外環境力只有波浪力。駁船參數如下:長Lpp=150.00m,寬B=50.00m,吃水T=10.00m,重心距基線高度KG=10.00m,排水量V=73 750m3,橫向慣性半徑kxx=20.00m,縱向慣性半徑kyy=39.00m,首搖慣性半徑kzz=39.00m。

模擬程序中的濾波部分采用非線性無源狀態觀測器。駁船的一階運動RAO和二階運動的QTF運用成熟的并應用廣泛的基于勢流理論計算軟件進行計算[15]。駁船的全回轉推力裝置布置圖如圖5所示，坐標系及推力器編號如圖6所示。

圖5 推力器分布

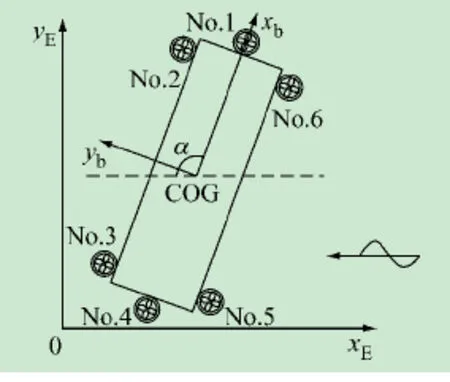
圖6 坐標系及推力器編號定義

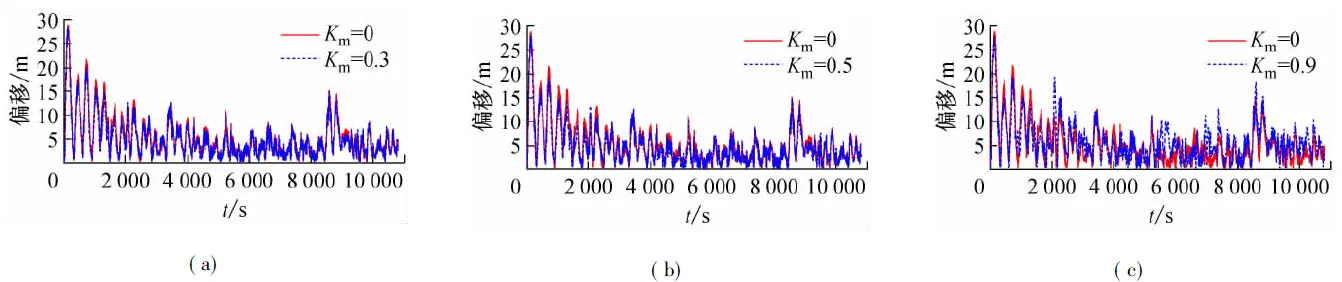
由圖5可以看出,裝備動力定位系統的駁船共有有6部全回轉推進器。 計算模型的全局和隨船坐標系定義見圖6。推進器的螺旋槳直徑3.6m，可以發出最大推力800kN。由于篇幅所限，時域模擬中采取了典型的β=60°和β=90°兩種環境力方向，波浪譜選用Jonswap譜，波浪譜峰周期13.4s，有義波高5.27m，譜峰因子3.3，在0～2rad/s的頻率范圍內取200個頻率。分別對駁船采用普通PID控制，即Km=0和帶有加速度反饋的PID控制進行了模擬，模擬時間10 800s，時間步長取1s。計算得到環境力方向β=60°時兩種控制模式下駁船位置偏移的比較時歷曲線如圖7所示。

(c)

由圖7觀察到，兩種控制模式下不同加速度增益值對駁船定位精度影響不同，在同一加速度增益值下對定位精度即瞬時偏移量進行比較，偏移量的峰值在有無加速度反饋項的兩種模式下交替出現，不能很好地觀察出其定位精度高低。對其不同加速度增益值時定位偏移量統計列表1。從表可見，在4種增益值中，Km=0.3時其平均偏移量由5.22減小了6.7%，在Km=0.5時偏移量減小了7.99%，這時其定位效果最好,即定位精度相對較高。進行縱向比較觀察到，相對的定位精度隨著增益值0～0.9是一個由低到高再到低的過程，甚至在增益值Km=0.9時，其平均偏差量甚至高于Km=0,即經典PID控制模式下的偏差。

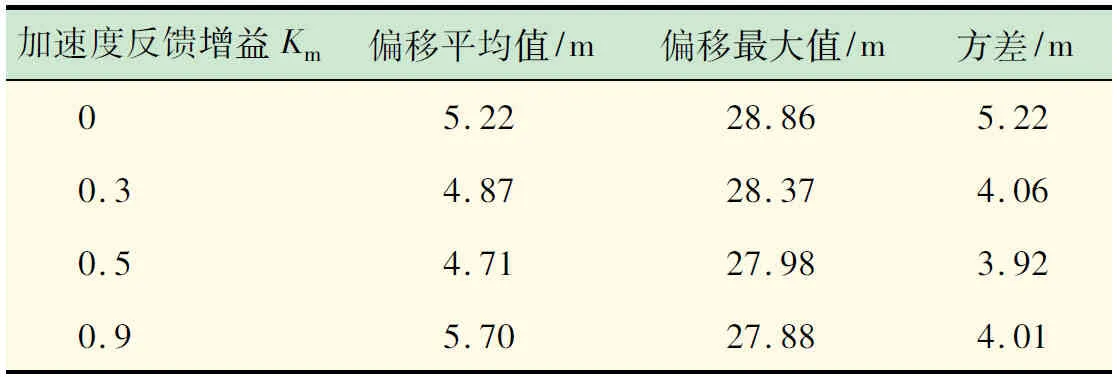
表1 不同加速度反饋增益下偏移位置統計(β=60°)

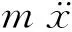
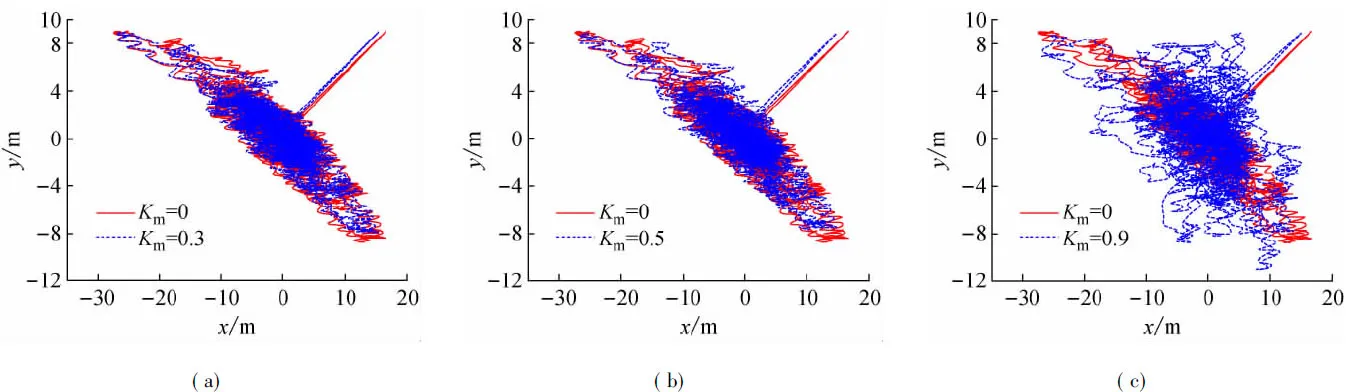
圖8 不同加速度反饋增益下駁船中心運動軌跡比較(β=60°)

從圖8中運動軌跡可以觀察出，Km=0.3和Km=0.5的加速度增益值相比較Km=0可以明顯改善定位精度。Km=0.9時，定位精度變差比較明顯。這也正好印證了上文提到的的理論說明。因此可以得出，在環境力方向β=60°時，隨著加速度增益值的增加，其駁船定位精度越來越高，但過大的加速度增益也會反過來影響定位精度，因此選取一個恰當的定位精度對于定位精度至關重要。

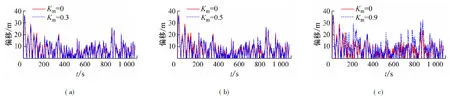
圖9 不同加速度增益下的位置偏移量比較(β=90°)

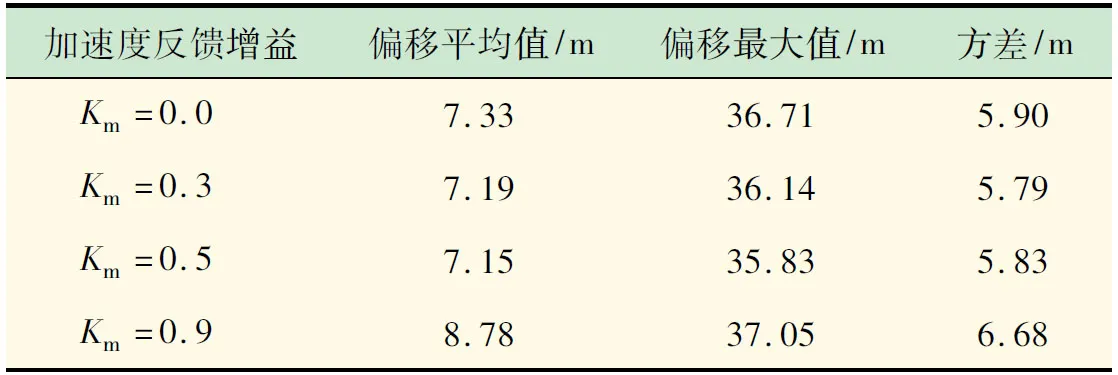
表2 不同加速度反饋增益下偏移位置統計(β=90°)

圖9和表2顯示了在環境力方向β=90°時，其偏移量即定位精度隨加速度增益值變化的情況。不難看出，在環境力方向β=90°整體的定位精度不如β=60°，同時其定位精度的規律與β=60°相同，定位精度隨著隨增益值的增加而增強，但在環境力瞬時變化不大時，過大的加速度增益反而使得控制系統高估了外力，從而降低了駁船定位精度，使得駁船的平均偏移值更大，例如Km=0.9時的偏移量統計很好地證明了這一點。下面給出β=90°遭遇橫浪時，駁船的中心移動軌跡，見圖10。由圖10可以得出與上文相同的結論。

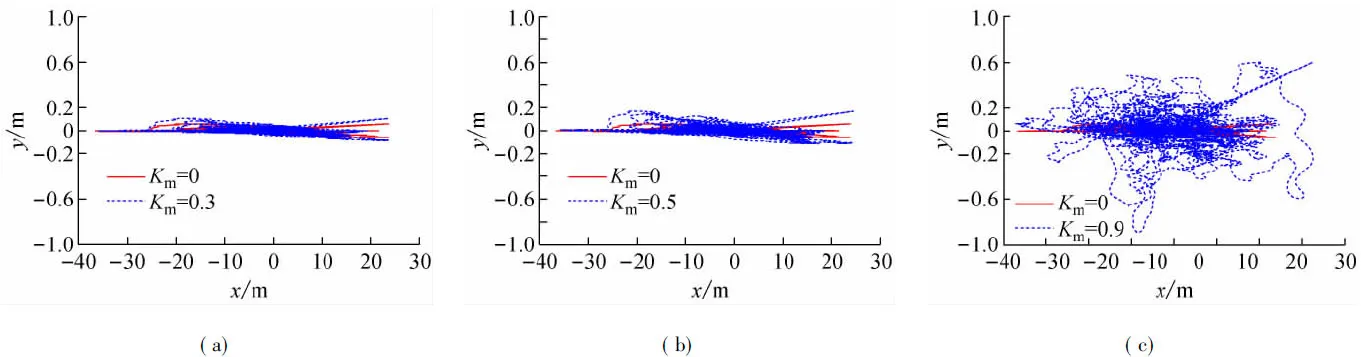
圖10 不同加速度反饋增益下駁船中心運動軌跡(β=90°)

綜上所述，經典PID控制方程中加入加速度反饋項對動力定位的定位精度有一定的提高與優化，特別是慣性較小的平臺或船舶，引入加速度反饋項可以起到給結構物增加虛擬質量的作用，從而提高定位精度，控制系統得到優化。但同時，過大的加速度反饋增益值將降低定位精度，因此選取恰當的加速度反饋增益對定位精度來說很重要。

3 結 論

首先針對Fossen教授設計的狀態觀測器進行了論述和數值模擬，由圖2可以看出，設計出的非線性無源狀態觀測器的重建與預估功能較好，能夠把接收的信號很好地估計出其中的低頻信號，并且沒有明顯的延遲現象。

針對傳統的PID控制方程中加入加速度反饋一項，并運用設計好的無源觀測器來進行時域數值模擬。由于篇幅受限，本文只選取斜浪β=60°和橫浪β=90°兩個方向，并分別設定加速度增益為0、0.3、0.5和0.9進行數值模擬并比較，得出如下結論：

(1) 環境力方向β=90°比β=60°時其定位精度要差，相同的加速度增益值兩種浪向定位精度進行比較，β=90°時的定位偏移量更大，精度更差。

(2) 在同一環境力方向時，隨著加速度增益值的增加，結構物定位精度也增加，系統得到優化，但增益值持續增加到過大時，定位精度反而降低。

(3) 選取適當的加速度反饋增益值很重要，在選取時要特別慎重，這關系到整個結構物定位精度的優劣。

通過本文分析與數值模擬，驗證文中設計的無源觀測器的濾波能力，同時分析比較在不同外環境力方向下，其加速度反饋增益值對動力定位精度的影響，希望對進一步系統優化提供一定的參考與借鑒。

[1] 金 秋，張國忠.世界海洋油氣開發現狀及前景展望[J].國際石油經濟，2005，13(3):43-44, 57.

[2] 趙志高，楊建民，王 磊,等.動力定位系統發展狀況及研究方法[J].海洋工程，2002，20(1):91-97.

[3] 余培文，陳 輝，劉芙蓉.船舶動力定位系統控制技術的發展與展望[J].中國水運(上半月)，2009(2):44-45.

[4] 丁福光, 譚勁鋒, 王元慧. 非線性濾波器在動力定位船位估計中的作用[J]. 中國造船, 2011,52(3): 67-73.

[5] Newman J N. Second Order, Slowly Varing Forces on Vessels in Irregular Waves[C]//Proceeding of Int Symp Dynamic of Marine Vehicles and Structures in Waves. London, 1974.

[6] 周 利, 王 磊, 陳 恒. 動力定位控制系統研究[J]. 船海工程, 2008, 37(2): 86-90.

[7] 信洪杰.船舶動力定位系統濾波及控位方法研究[D].哈爾濱:哈爾濱工程大學，2012.

[8] 德 華，徐海祥，李文娟,等.基于非線性無源濾波器的船舶動力定位仿真[J].武漢理工大學學報，2013，35(10):69-73.

[9] Fossen T I, Strand J P. Passive nonlinear observer design for ships using Lyapunov methods: full-scale experiments with a supply vessel[J]. Automatica, 1999, 35(1): 3-16.

[10] 李 博. 動力定位系統的環境力前饋研究[D].上海:上海交通大學, 2013.

[11] Fossen T I. Handbook of Marine Craft Hydrodynamics and Motion Control[M]. NJ: John Wiley & Sons, 2011.

[12] Fossen T. Marine Control Systems, Guidance, Navigation and Control of Ships, Rigs and Underwater Vehicles[M]. NJ: Marine Cybernetics, Trondheim, Norway, 2002: 29.

[13] Kristiansen E, Hjulstad A, Egeland O. State-space Representation of Radiation Forces in Time-domain Vessel Models[J]. Ocean Engineering, 2005,32: 2195-2216.

[14] Skejic R, Faltinsen O M. A Unified Seakeeping and Maneuvering Analysis of Ships in Regular Waves[J]. Journal of Marine Science and Technology, 2008, 13(4): 371-394.

[15] 王 亮. 深海半潛式鉆井平臺動力定位能力分析[D]. 上海: 上海交通大學, 2010.

On Acceleration Feedback Control of Vessel Dynamic Positioning System

ZHANGTao,WANGLei,WANGHong-chao

(State Key Laboratory of Ocean Engineering, Collaborative Innovation Center for Advanced Ship and Deep-sea Exploration, Shanghai Jiaotong University, Shanghai 200030, China)

In this research a passive observer designed by Professor Fossen is used to simulate numerically state. Based on the valid observer, an acceleration term is added to the control system. A barge is selected as the simulation object. The barge is simulated with 60° and 90° wave directions and different acceleration gains. In conclusion, when the wave angle is 60°, the position accuracy of barge is better than that of the wave angle 90°. When the barge is in the same wave angle, the positioning accuracy becomes better with the acceleration gain increase from 0. However, the positioning accuracy can be down if the gain exceeds certain value. So the appropriate acceleration gain can enhance the positioning capability of floating structures. And for the small mass floating structures, adding the acceleration term can improve the positioning accuracy effectively by choosing proper gains.

passive observer; PID controller; acceleration feedback; numerical simulation

2015-05-04

國家自然科學基金項目(51179103)；中國國家重點基礎研究進展計劃項目(2013CB036103)

張 濤(1989-)，男，黑龍江哈爾濱人，碩士生，主要從事動力定位研究。

王 磊(1971-)，男，安徽蚌埠人,副教授，碩士生導師，主要從事動力定位系統的研究。

Tel.：021-62932025；E-mail：wanglei@sjtu.edu.cn

P 751

A

1006-7167(2016)01-0004-06