基于CAViaR模型的滬深300股指期貨隔夜風險研究

簡志宏，曾裕峰，劉曦騰

(1.華中科技大學經濟學院，湖北 武漢 430074；2.復旦大學經濟學院，上海 200433； 3.上海財經大學公共經濟與管理學院，上海 200433)

?

基于CAViaR模型的滬深300股指期貨隔夜風險研究

簡志宏1，曾裕峰2，劉曦騰3

(1.華中科技大學經濟學院，湖北 武漢 430074；2.復旦大學經濟學院，上海 200433； 3.上海財經大學公共經濟與管理學院，上海 200433)

期貨隔夜風險的防范歷來是投資者關注的熱點，本文以滬深300股指期貨為研究對象，采用CAViaR模型對普通隔夜風險進行度量，同時還采用新建的CAViaR-EVT模型對極端隔夜風險進行預測，全面地分析了多頭VaR和空頭VaR在不同分位數的動態變化特征，最后采用Kupiec似然比檢驗和動態分位數檢驗對模型進行后測檢驗。實證結果表明，隔夜收益序列具有右偏、無長期記憶性和尖峰厚尾等典型特征；CAViaR模型對股指期貨的普通隔夜風險具有優異的預測能力，其中AS模型的預測效果最好；加入極值理論后，CAViaR-EVT模型同樣能很好地刻畫極端分位數下隔夜風險的動態演化過程，且其預測結果比EVT和GARCH-EVT模型要更合理。

隔夜風險；CAViaR模型；滬深300股指期貨；VaR

1 引言

2010年4月16日我國正式推出滬深300股指期貨，填補了我國金融期貨的空白。經過五年的孕育成長，目前已成為我國交易量最大的期貨品種。由于我國股指期貨市場還沒有采用連續交易機制，因而可分為交易時間和休市時間。在交易時間內投資者可以自由地進行競價買賣，但是白天交易結束后，投資者當天買入的頭寸在第二天開盤前處于敞口狀態，而恰恰此期間是上市公司信息公告發布的密集區[1],如果新信息進入市場，那么它對價格的累計影響將會直接反映到第二天的開盤價，從而使得股指期貨的開盤價出現“跳空上漲”或“跳空下跌”。本文將投資者持有的頭寸在當天休市前未能及時平倉，從而給投資者帶來隔夜損益的不確定性稱為隔夜風險。在實務界,市場參與者都將其視為不確定性的大源頭(特別是在我國期貨市場)，期貨是一種高杠桿化的金融衍生產品，隨著期貨價格對于信息反映的時滯越來越短，加之當前國際金融市場不穩定因素越來越多，因此,一旦休市期間期貨市場遭遇到不利的外部沖擊，投資者持有的頭寸會在開盤瞬間發生跳躍性變動，從而會給投資者帶來巨大風險，甚至出現爆倉的可能性。所以，無論是對股指期貨市場的各類投資者還是我國的金融監管當局而言, 對股指期貨隔夜風險的波動特征和風險狀況進行準確的刻畫和科學的預測, 進而探索有效的期指市場風險防范和監控手段, 都具有非常重要的現實意義。

在理論界，由于交易數據的限制和相關理論的不成熟，使得隔夜信息一直沒有得到足夠的重視。直到Andersen和Bollerslev[2]首次提出用高頻數據的日內收益率平方和來估算已實現波動率。眾多學者才開始關注隔夜波動率，并將隔夜波動率視為日內已實現波動率的延續，兩者之和才構成日已實現波動的最優測度[3-4]。Taylor[5]利用條件波動的線性回歸模型評價了1998-2002年S&P500期貨市場隔夜交易的預測能力，并論證了含隔夜信息模型的波動預測能夠帶來更準確的風險價值測度。Andersen等[6]認為隔夜收益是整日收益的重要組成部分，可將其看作是動態相依的跳躍時間序列，并基于GARCH-t模型對美國期貨的高頻數據分析，結果表明日內連續性波動對隔夜波動具有顯著的對稱解釋能力，而日內跳躍性波動解釋效果不顯著。近幾年國內已有學者開始關注隔夜信息，如劉慶富和張金清[7]基于隨機波動模型檢測了商品期貨隔夜信息對日間交易的影響，實證結果發現總隔夜收益對日間收益及其波動均具有顯著的預測能力。簡志宏和李彩云[8]采用HAR-CJ-M模型對我國滬深300股指的隔夜收益波動率直接建模分析，結果發現大的隔夜波動率具有波動聚集性且可以被預測，但小的隔夜波動是市場微觀噪聲造成，不具備可預測性。上述國內外研究主要闡述了隔夜信息的重要性和隔夜波動率的可預測性，但是目前國內還沒有以股指期貨隔夜收益為直接研究對象，更沒有將隔夜風險納入到VaR理論體系內進行風險管理的文獻。

Engle和Manganelli[9]創造性地直接對VaR進行自回歸建模，提出了CAViaR(Conditional Autoregressive Value at Risk)模型，由于該方法不對收益分布做任何假設，并且對于具有尖峰厚尾、長記憶性和非對稱性等典型事實的金融數據而言，該方法具有明顯的優勢，因此自提出以來在國內外得到了廣泛的應用。Huang Dashan等[10]用改進的CAViaR模型考察了WTI現貨石油收益對VaR的不對稱的影響，并使用混合數據回歸模型(Mixed Data Regression Model)預測了石油價格的多期VaR值。Huang Dashan等[11]基于模型系數與宏觀經濟變量聯動性的事實，提出系數時變的指數興奮CAViaR(Index-Exciting CAViaR)模型，實證結果表明該模型在市場之間存在溢出效應時表現最佳。閆昌榮[12]通過構造流動性調整的CAViaR模型，從而為投資者提供了一個流動性風險管理的有效途徑。陳磊等[13]將AS-CAViaR模型的一階自回歸項進行門限分解，提出新的TCAViaR模型，更好地分析了石油期貨左尾和右尾不同分位數下尾部風險影響因素的差異。同時，陳磊等[14]為避免傳統CAViaR模型的估計風險和模型風險，構造出貝葉斯CAViaR模型，該模型顯著地提高了布倫特原油油價的VaR預測績效。可見CAViaR模型在相關的金融風險管理研究中已經得到了很好的運用，考慮到股指期貨的隔夜收益是瞬時的收益序列，它不存在微觀的交易信息，因此采用高頻數據的VaR方法根本行不通，而且CAViaR模型避免了GARCH族模型求解波動率和殘差分布等復雜的變量，因此為刻畫隔夜風險的動態變化提供了獨特的視角。

就目前已有的國內國外文獻，實質意義上對隔夜風險進行研究的文獻僅有一篇，即簡志宏和李彩云[8]的研究。該文章用隔夜波動來度量隔夜風險，然而方差風險對高出均值的投資結果和低于均值的投資結果賦予相同的權重，難以符合實際，現實生活中投資人的效用函數中常對損失帶來的負效用施以更大的權重，對收益帶來的正效用給予較小權重，而本文采用VaR理論來度量隔夜風險；其次，該文是針對滬深300指數的隔夜風險進行分析，而本文是針對股指期貨進行分析，實踐意義可能更重大。總之，本文的研究角度和方法與之均不相同。為了更好地完善現有的文獻，本文有以下幾點貢獻：首先，本文創新性地將股指期貨的隔夜風險納入到VaR風險管理的分析框架下，并嘗試用CAViaR模型去度量滬深300股指期貨隔夜風險；其次，將極值理論和CAViaR模型結合起來構造新的CAViaR-EVT模型，并對極端隔夜風險進行預測，有效地克服了現有模型的不足；最后，同時考慮了隔夜風險的左尾分位數和右尾分位數的變化特征，對具有買空賣空交易的期貨市場而言，分析角度更加全面、現實意義更重大。

2 數據來源及描述性統計

本文選取的數據為滬深300股指期貨市場2010年4月16日到2015年5月18日的實時交易數據。我國滬深300股指期貨有當月、下月、下季和隔季四個期貨合約，但當月連續的期貨合約交易最活躍，因此本文選用當月連續合約的日度數據來構造連續收益序列，最后總共得到1232個有效的交易日數據，其中前732個數據作為樣本內數據，最后500個數據作為樣本外后測檢驗使用。數據均來源于Wind數據庫。

目前我國滬深300股指期貨市場還沒有實行連續交易，所以整日收益率可分解為隔夜收益率和日內收益率兩個部分，隔夜收益率通過當日開盤價與前一日收盤價的對數差分求解而來，為了更清晰的表述，具體如圖1所示。

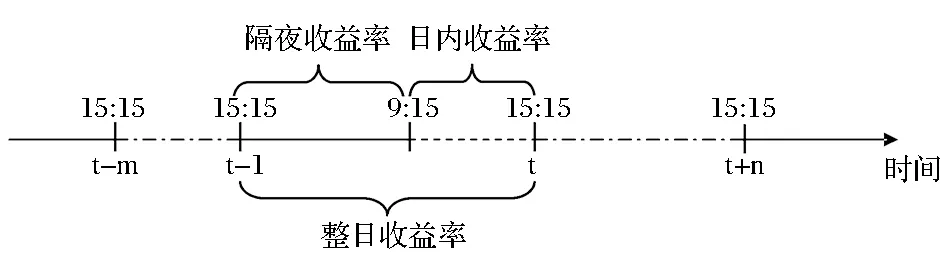
圖1 日收益率的構成

通過對隔夜收益率的原始統計和描述性結果發現，隔夜收益率的均值為0.038，且隔夜收益為正的天數達到670天，開平盤(指當天的開盤價和昨日的收盤價相同，由原始數據計算得出)的天數為29天，這在一定程度上表明股指期貨開盤總體趨向跳空上漲，隔夜收益最大值和最小值分別為4.486和-3.535，由于我國股指期貨是采用10%的保證金比例交易，那么杠桿化后的隔夜收益變動將被進一步放大，這充分說明了股指期貨潛在隔夜風險不容忽視且有研究的必要性。偏度系數和超額峰度系數均在1%水平下顯著，說明隔夜收益序列具有右偏和“尖峰厚尾”的性質。J-B統計量和QQ圖的結果顯示隔夜收益率具有顯著的非正態性質。Ljung-Box Q統計量和ADF單位根檢驗結果顯示隔夜收益率是不具有長記憶的平穩序列。

表1 隔夜收益描述性統計

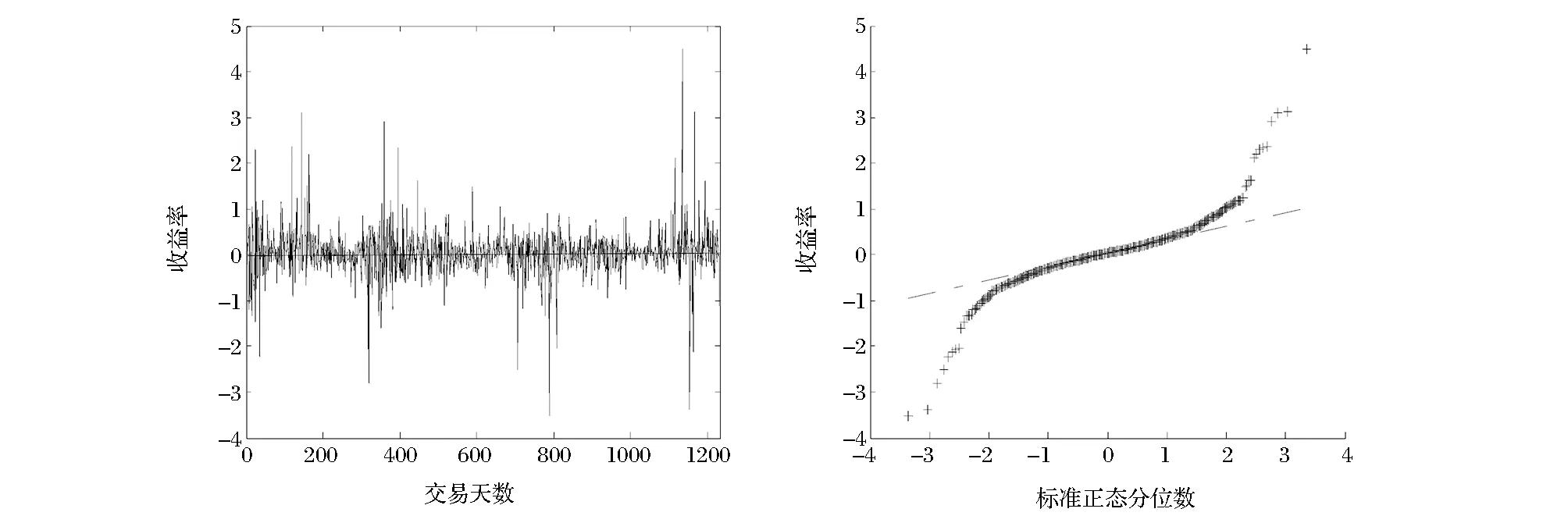
圖2 滬深300股指期貨隔夜收序列圖和QQ圖

另外，從圖2明顯可以看出，自滬深300股指期貨上市至今主要有四個波動劇烈的區間：2010年4月份股指期貨在剛推出時隔夜風險的波動較大，這可能是由于股指期貨剛推出，市場上參與股指期貨交易者以噪聲交易者為主，投資主體不理性的交易行為導致隔夜波動較大；2011年8月份左右，股市大量資金出逃，出現嚴重的“錢荒”現象，A股市場疲軟；2013年7月份左右，A股市場的增發配股、股權再融資和發債融資出現井噴之勢，使得市場恐慌、投資者擔憂再起，股市節節走低；2014年11月份開始，我國央行出臺了寬松貨幣措施，市場投資者信心得到了提振，房市價格得到較好的控制，大量資金進入股市，使得整個股市的流動性非常充裕。

3 隔夜風險測度模型及估計結果

3.1 CAViaR模型

Engle和Manganelli[9]認為既然股票收益具有序列自相關性，而VaR的本質就是收益率序列的某一特定分位數，從而提出條件自回歸風險價值模型(即CAViaR模型)對收益條件分位數直接建模。并給出了四種特殊形式的CAViaR模型，其中Adaptive模型在實證結果中表現最差，且被拒絕的概率最大。因此本文主要側重于分析以下三個模型：

SAV-CAViaR模型：ft(β)=β1+β2ft-1(β)+β3|yt-1|

(1)

AS-CAViaR模型: ft(β)=β1+β2ft-1(β)+β3(yt-1)++β4(yt-1)-

(2)

(3)

其中，(yt-1)+和(yt-1)-分別表示滯后一期收益率的正部和負部，ft(β)表示收益率的條件分位數。方程(1)和(3)假設過去正負收益對未來風險的影響是對稱的，AS-CAViaR模型本質上是SAV-CAViaR模型的一般形式，它反映了正負收益率對未來風險的非對稱效應。

3.2 模型的估計結果

上述SAV-CAViaR模型、AS-CAViaR模型和IGARCH模型的估計均需要使用分位數回歸(Quantile Regression)，分位數回歸的思想最早由Koenker和Bassett[15]提出，它是最小絕對離差(Least Absolute Deviation，LAD)模型的特殊情形。Engle和Manganelli[9]采用Nelder-Mead simplex和quasi-Newton最優化算法估計上述模型參數，具體要優化的目標函數為：

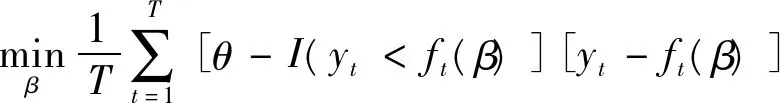
(4)

其中，θ表示回歸的樣本分位數。相比均值回歸，它能充分刻畫自變量X對于因變量Y分布的位置、刻度和形狀的影響。在殘差序列服從高斯分布的情況下，分位數回歸的估計效率只有很小的損失；針對不服從正態分布的時間序列，特別是對具有“尖峰厚尾”性質的金融收益序列，它能準確地捕捉到分布的尾部特征，因而使得分位數回歸系數估計比普通最小二乘法具有更強的穩健性。

由于在我國股票市場賣空交易受到諸多限制，因此在相關的文獻中一般選擇左尾分位數(如1%和5%)來對未來風險進行VaR預測，但在滬深300股指期貨市場中有多頭和空頭之分，期貨價格上漲和下跌都會給相關頭寸持有者造成損失，因此本文將兩者結合起來共同分析，其中1%、5%和10%水平的分位數可以作為股指期貨多頭持有者所面臨的風險，簡稱為多頭風險；而99%、90%和95%分位數可以表示股指期貨空頭頭寸持有者面臨的風險，簡稱為空頭風險。

在模型的參數估計中，取收益序列前300個觀測值的θ經驗分位數來初試化f1(β)。RQ值為目標優化函數(4)估計值。樣本內DQ統計量主要是用來檢驗模型對樣本內數據的擬合程度，當樣本內DQ統計量的P值小于顯著性水平0.05時，則拒絕該模型；反之，則接受該模型。樣本內DQ統計量和

下文樣本外DQ統計量有一定的差異性，具體解釋可見Engle和Manganelli[9]。

由表2和表3可得出以下結論，第一，從樣本內DQ檢驗結果來看，右尾所有模型都通過了DQ檢驗，而左尾只有AS模型全通過了DQ檢驗，說明CAViaR模型對刻畫隔夜風險的右尾更具有優勢，另外，AS模型又要比SAV模型和IGARCH模型更優異；第二，各模型在相同分位數下的RQ值相差不大，但AS模型在所有分位點水平下均具有最小的RQ值；第二，系數β2基本上都是高度顯著的，這說明尾部分位數的波動聚集效應是顯著存在的，而且它的值均保持在0.8以上，尤其是右尾β2的取值均在0.94以上，這說明了VaRt具有非常強的短期記憶性，且右尾比左尾的強度更大；第三，針對外部沖擊不具有非對稱效應的SAV模型和IGARCH模型，右尾系數β3在0.1的顯著性水平下均顯著，而左尾系數β3部分顯著，說明外界信息沖擊對于未來隔夜收益的分位數預測具備相當的解釋能力，但在左、右尾的表現具有明顯的差異。一旦將外部沖擊分解為正面和負面收益消息時，β3系數在左尾分位數上部分顯著，在右尾分位數全部顯著，而β4系數絕大部分是顯著的，這在一定程度說明多頭方和空頭方在對待外界消息沖擊時的敏感程度是不一致；第四，針對非對稱結構的AS模型，從外界消息沖擊對當期VaR的影響方向來看，股指隔夜收益的上漲和下跌均會加大下一期的VaR值，換言之，隔夜收益的上漲和下跌會顯著地加大下一期的隔夜風險。

總而言之，無論是從RQ值和樣本內DQ統計量值，我們發現具有杠桿效應的AS模型要比SAV模型和IGARCH模型表現更佳，它能更好地描述普通隔夜風險的動態特征。

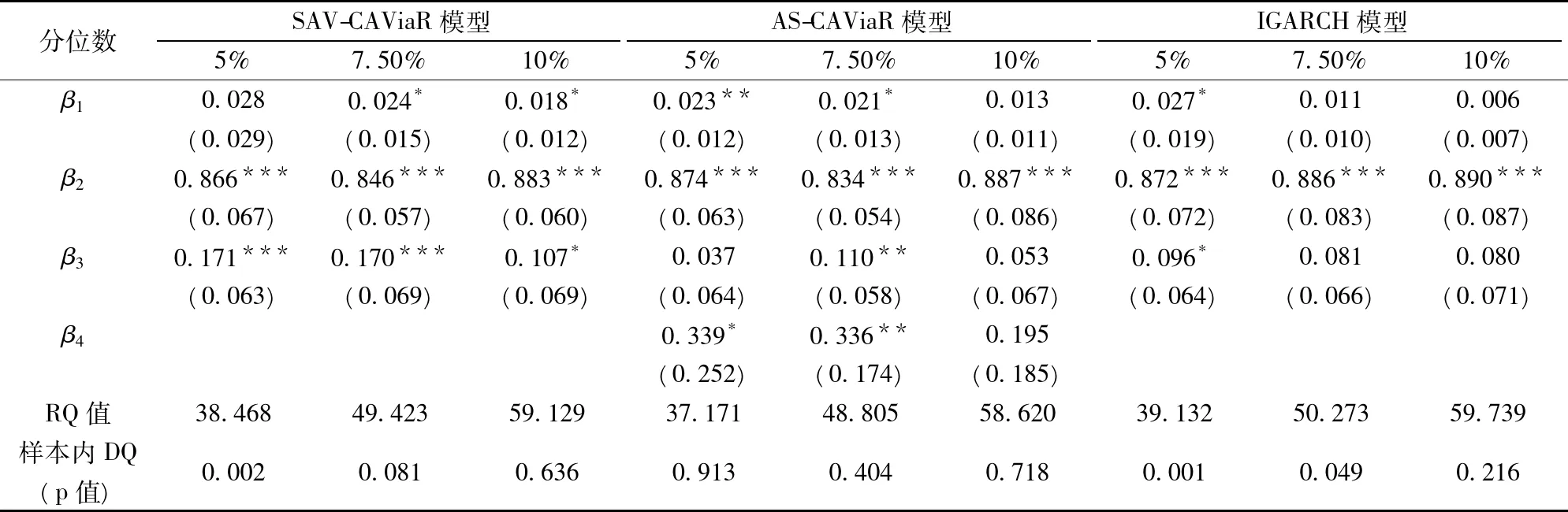
表2 模型左尾分位數估計結果

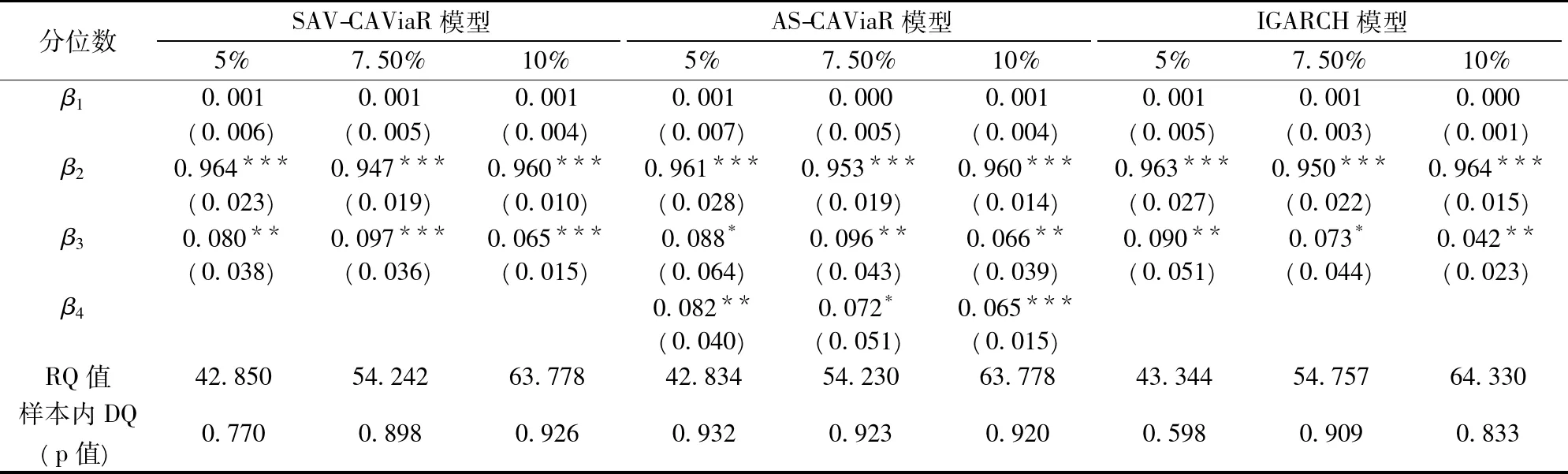
表3 模型右尾分位數估計結果

4 模型的后測檢驗方法及結果分析

4.1 后測檢驗方法說明

為了檢驗上述各模型的樣本動態VaR預測精度，Kupiec[16]提出了一種VaR失敗率(Failure Rate)的似然比檢驗方法，為了進行該檢驗，首先定義“擊中序列”(Hit Sequence)hitt,以多頭VaR為例，定義如下：

(5)

它表示的是，如果t時刻的實際收益超出所估計的VaR值，稱為一次擊中事件，那么該序列t時刻的取值為1，否則為0。假設該模型能有效地預測隔夜風險，則該“擊中序列”應服從貝努利分布。在模型沒有誤設的零假設下，構造似然比的非條件檢驗統計量：

(6)

其中，p為顯著性水平，N為預測的樣本總數，n為預測樣本中的失敗次數。通過(6)式可知道Kupiec檢驗量是刻畫實際失敗次數接近理論失敗次數程度的指標。當LR統計量大于給定置信水平下卡方分布的臨界值，則拒絕原模型。相反，當統計量小于臨界值，則接受該模型。

但是，Kupiec似然比檢驗只是檢驗實際擊中比率與理論擊中比率的接近程度。進一步的研究表明，除了檢驗失敗比率以外，還應檢驗VaR失敗值之間是否存在相關性[9,17]，如果發生VaR預測失敗的觀測值之間具有明顯的相關性，那么有可能發生連續超過VaR的損失，這將給投資者帶來巨大的損失，也就是說，精確可靠的風險測度模型的擊中序列應該是無偏和無自相關的。由此，Engle和Manganelli[9]提出了動態分位數檢驗(Dynamic Quantile test，DQ test)，以多頭風險為例，該檢驗首先定義一個新的擊中序列：

HITθ,t=I(yt<-VaRt)-θ

(7)

其中，θ為給定的分位數，當yt<-VaRt時，HITθ,t=1-θ；當yt>-VaRt時，HITθ,t=-θ。顯然，如果模型參數估計正確，那么E(HITθ,t|Ωt-1)=0。這說明HITθ,t對于任何滯后的HITθ,t-k以及預測的VaRt-k都應不具備相關性，構造如下回歸方程：

HITθ,t=β0+β1HITθ,t-1+β2HITθ,t-2+……+βpHITθ,t-p+βp+1VaRt+ut

(8)

把上述模型表述成矩陣形式：HITθ,t=Xβ+ut，其中X是T×K矩陣向量，借鑒淳偉德等[18]的做法，取p=5,k=7。在原假設：β=0的情況下，構造的DQ檢驗統計量為：

(9)

4.2 普通隔夜風險的后測檢驗分析

從表4兩個后測檢驗結果可以看出：在5%的顯著性水平下，三個模型僅在0.95的分位數下均無法通過樣本外DQ檢驗，似然比檢驗則全部通過，說明本文給出的這三個CAViaR模型整體能很好地描述常規分位數水平上隔夜風險的動力學特征；在表4相應的12組估計結果中，AS模型只獲得6次并行的最優風險預測精度，IGARCH獲得5次，SAV模型則只有3次，結合表(2)(3)的估計結果可知，AS模型在普通分位數的多空頭VaR預測方面表現最優。而SAV模型和IGARCH模型整體表現次之，兩者無絕對的優劣之分。

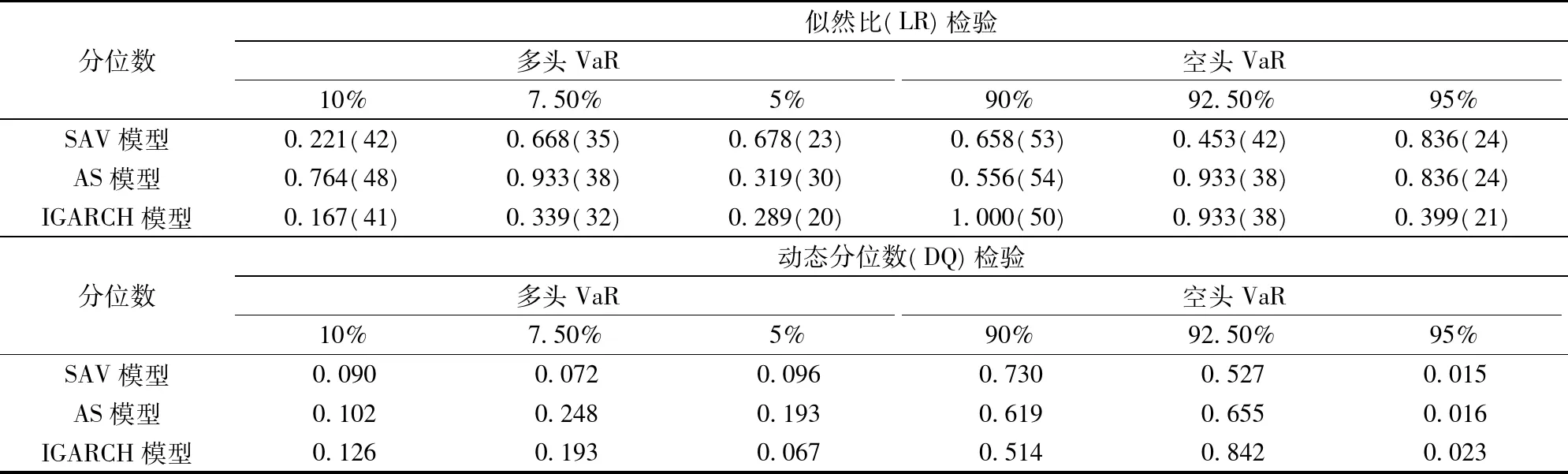
表4 模型的后測檢驗結果

5 極端隔夜風險的預測

對于極端分位數(如0.5%或0.1%)的估計，由于半參數CAViaR模型進行最優化時可利用的數據極少，如果直接采用CAViaR模型對低分位數VaR進行估計，勢必會造成結果不可靠乃至偏差。目前國內針對極端尾部風險度量的方法主要有EVT-POT和GARCH-EVT兩種，但是極值理論要求原始數據為獨立同分布，且閾值的選擇具有一定的主觀性，而金融收益數據往往難以滿足其要求；GARCH-EVT模型雖然對原始收益數據進行了一定程度的過濾，但究竟選擇何種收益分布和波動率方程目前也沒有共識。為此，Manganelli和Engle[19]在理論上構建CAViaR-EVT模型，但該模型仍未用于實證研究，該方法結合了CAViaR模型處理常規分位數的優勢，以及極值理論處理尾部風險的穩健性，因此該模型在計算低分位數風險價值時更具可靠性。由于極端隔夜風險對于期貨投資者而言意義重大，如不能很好的防范將遭受巨大的損失，因此這部分采用CAViaR-EVT模型對極端隔夜風險進行分析預測。

5.1 CAViaR-EVT模型的構建

為節省篇幅，本文以左尾分位數為例(右尾推導過程類似)，具體闡述CAViaR-EVT模型估算極端隔夜風險的步驟如下：

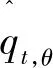
(10)

然后，由于標準化的殘差序列有效地削弱了原始數據的自相關性，因此更適合運用極值理論。現僅假設標準化的分位數殘差序列右尾具有獨立同分布性質，通過(11)可將求解原始收益數據的p分位數轉換為求解標準化殘差序列的(1-p)分位數：

Pr(ytqt,p/qt,θ-1)=p

(11)

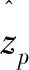
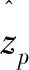
(12)

其中ξ代表形狀參數，而σ代表尺度參數，ξ>0時說明廣義帕累托分布是厚尾的。當尾部數據很少時，POT仍然具有較強的穩健性，因而本文考慮使用EVT中的POT模型對極端尾部進行建模分析。

POT模型關鍵是確定最優的門檻值，閾值的選取通常有兩種方法：一是根據Hill圖；二是依據超額期望函數圖。本文采用第二種方法。將樣本值按從大到小排列，即X(1)>X(2)>…>X(n)，樣本的超額期望函數定義為：

(13)

確定閾值后，超過閾值u的超額數分布函數為:

(14)

對于充分高的閾值，超過閾值的數據近似服從GPD分布(Generalized Pareto Distribution)，即有Fu(y)≈Gξ,σ，由(14)式可得分布的尾部累積分布函數為：

F(x)=(1-F(u))Gξ,σ(x-u)+F(u) (x>u)

(15)

假設超過閾值的樣本個數為Nu,總樣本數為n，采用(n-Nu)/n替換F(u)，并運用極大似然法估計出相關的參數ξ、σ，最后經過相關推導可得到置信水平p下的VaR值：

(16)

5.2 極端隔夜風險的后測檢驗分析

利用POT方法計算VaR時首先必須確定適當的閾值，選擇合適閾值的標準是使得超限期望函數在大于閾值時近似為正斜率的線性函數，根據公式(13)，得到隔夜收益的標準化殘差序列的超限期望圖，從而確定最優閾值，再使用極大似然估計方法求出GPD分布的參數。表5給出了由(15)計算出的標準化殘差序列的相關估計結果，可以看出，閾值u在[0.0178，0.0498]區間，系數ξ在所有模型中均為正，說明標準化殘差序列具有顯著的厚尾性。

求得上述結果后，利用(16)式得到標準化殘差序列的VaR值，最后根據殘差與原始序列的關系得出隔夜收益對應置信水平下的VaR值。

表5 標準化殘差序列EVT-POT估計結果

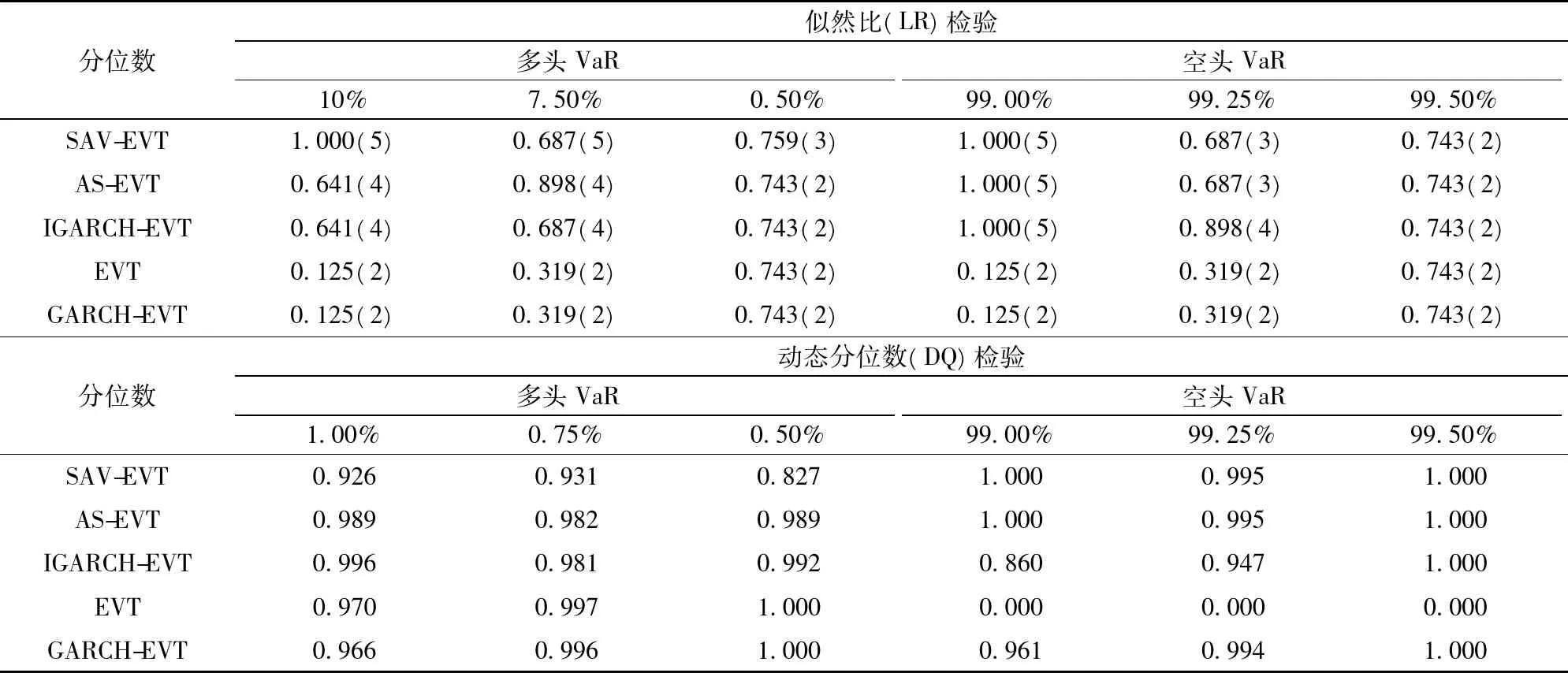
表6 極端分位數的后測檢驗結果

為了進行簡單的對比，表6給出了CAViaR-EVT模型、EVT和GARCH-EVT三種不同模型的后測檢驗結果：(1)從Kupiec似然比檢驗結果來看，所有模型在95%的置信水平下均拒絕原模型；然而，動態分位數檢驗結果不如Kupiec 似然比檢驗理想，EVT模型對右尾的三個分位數上都被拒絕，但其他的分位數都高度顯著，至于DQ檢驗出現很多相同的P值，且P值的波動性相當大，主要是因為CAViaR模型在預測極端分位數下VaR出現的失敗次數很少，甚至為0，最終使得HITθ,t序列容易出現強自相關或無自相關這兩種極端的情況；(2)CAViaR-EVT中的三個模型通過了所有的后測檢驗，且預測精確度表現優異，但三者之間沒有哪一個模型展現出絕對的優勢，三者均能良好的刻畫我國股指期貨極端隔夜風險的動態變化過程。由于CAViaR模型無須設定誤差分布函數的特定形式，在計算普通分位數的VaR表現優異，而EVT-POT方法能準確捕捉尾部分布特征，兩者的結合更有利于準確分析極端事件對金融市場造成的沖擊和影響；(3)從似然比檢驗的失敗次數來看，基于EVT 的靜態VaR 模型在估計風險時過于保守，過高估計了風險，造成了資金使用的無效率，同時它也無法規避VaR擊中事件的相關性問題。GARCH-EVT模型也存在高估隔夜風險的問題。總體而言，本文提出的CAViaR-EVT模型的預測精度要優于EVT和GARCH-EVT模型，它能更準確分析極端事件對金融市場造成的沖擊和影響，以便預測極端波動風險。

6 結語

滬深300股指期貨作為我國交易最活躍的期貨品種，其隔夜風險測度和防范一直是企業界和監管部門關注的熱點。本文以滬深300股指期貨當月連續合約為例，深入研究了隔夜收益的統計特征及波動模式，并采用了半參數法的CAViaR模型刻畫了滬深300股指期貨多頭和空頭在不同分位數的VaR動態特征，并首次運用CAViaR-EVT模型來對極端隔夜風險進行預測，最后運用后測檢驗中的Kupiec似然比檢驗和動態分位數檢驗對不同風險模型的測度精度進行比較。通過實證得出以下結論：

第一，從整個樣本期變動趨勢看，隔夜收益在上市前期表現出較大的價格波動，后期則日趨平穩，而后又出現階段式的大幅波動。從隔夜收益序列自身特性來看，它呈現出右偏和尖峰厚尾特性、缺乏長期記憶性，且跳空上漲的概率比跳空下跌的概率要大等性質。

第二，CAViaR模型對我國股指期貨市場的普通隔夜風險具有優異的預測能力。通過嚴謹的后測檢驗結果看出，AS模型在預測普通隔夜風險上要優于IGARCH模型和SAV模型，而SAV模型和IGARCH模型之間無明顯的優劣之分。

第三，為了預測極端分位數下的隔夜風險VaR，本文巧妙地結合極值理論和CAViaR方法的優勢構造出CAViaR-EVT模型，通過與EVT和GARCH-EVT模型對比發現，該模型對動態極端隔夜風險VaR同樣具有良好的預測精度。

目前我國期貨市場相比發達的期貨市場而言還處于初步發展階段，制度不完善、國際定價權缺乏和投機心理嚴重，使得我國期貨市場極易受到復雜多變的國際國內金融環境影響。而且期貨作為一種金融衍生產品，其面臨的隔夜風險會被成倍的放大，那么如何有效地管理隔夜風險必定是業界和理論界密切關注的熱點。值得一提的是，本文采用的CAViaR模型在一定程度上能夠很好的度量和預測滬深300股指期貨普通隔夜風險和極端隔夜風險，文中的結論有助于投資主體更好地認識隔夜風險，也可以為中國股指期貨投資者和監管部門開展有效的風險管理及監督活動提供理論參考。

[1] Del C W, Colwell D, Michayluk D, et al. News releases when markets are closed[R].Working Paper, University of Technology Sydney, 2003.

[2] Andersen T G, Bollerslev T. Answering the skeptics: Yes, standard volatility models do provide accurate forecasts[J].International Economic Review, 1998, 39(4)：885-905.

[3] Hansen P R, Lunde A. A realized variance for the whole day based on intermittent high-frequency data[J].Journal of Financial Econometrics, 2005, 3(4)：525-554.

[4] Koopman S J, Jungbacker B, Hol E. Forecasting daily variability of the S&P 100 stock index using historical, realised and implied volatilitymeasurements [J].Journal of Empirical Finance, 2005, 12(3)：445-475.

[5] Andersen T G, Bollerslev T, Huang Xin. A reduced form framework for modeling volatility of speculative prices based on realized variation measures[J].Journal of Econometrics, 2011, 160(1)：176-189.

[6] Taylor N. A note on the importance of overnight information in risk management models [J].Journalof Banking & Finance, 2007,31(1)：161-180.

[7] 劉慶富,張金清.中國商品期貨隔夜信息對日間交易的預測能力[J].管理科學學報,2013, 16(11)：81-94.

[8] 簡志宏,李彩云.隔夜風險可以預測嗎?——基于HAR-CJ-M模型的高頻數據分析[J].管理評論,2014,26(2)：5-14.

[9] Engle R F，Manganelli S. CAViaR: Conditional autoregressive value at risk by regression quantile[J].Journal of Business and Economic Statistics, 2004, 22(4)：367-381.

[10] Huang Dashan, Yu Baimin, Fabozzi F J, et al. CAViaR-based forecast for oil price risk[J].Energy Economics, 2009, 31(4)：511-518.

[11] Huang Dashan, Yu Baimin, Lu Zudi, et al. Index-exciting CAViaR: A new empirical time-varying risk model[J].Studies in Nonlinear Dynamics & Econometrics, 2010, 14(2)：1-24.

[12] 閆昌榮.基于流動性調整CAViaR模型的風險度量方法[J].數量經濟技術經濟研究，2012，(3)：151-161.

[13] 陳磊,曾勇,杜華宇.石油期貨收益率的分位數建模及其影響因素分析[J].中國管理科學，2012,20(3)：35-40.

[14] 陳磊,杜化宇,曾勇.基于貝葉斯CAViaR模型的油價風險研究[J].系統工程理論與實踐,2013,33(11)：2757-2765.

[15] Koenker R, Bassett Jr G. Regression quantiles[J]. Econometrica, 1978, 41(1)：33-50.

[16] Kupiec P H. Techniques for verifying the accuracy of risk measurement models[J].Journal of Derivatives, 1995, 3(2)：73-84.

[17] 魏宇.基于多分形理論的動態VaR預測模型研究[J].中國管理科學,2012,20(5)：7-15.

[18] 淳偉德,陳王,潘攀.典型事實約束下的上海燃油期貨市場動態VaR測度研究[J].中國管理科學,2013,21(2)：24-31.

[19] Manganelli S, Engle R F. Value at risk models in finance[R]. Working Paper,Frankfurt am Main: European Central Bank, 2001.

[20] McNeil A J, Frey R. Estimation of tail-related risk measures for heteroscedastic financial time series: An extreme value approach [J].Journal of Empirical Finance, 2000, 7(3)：271-300.

[21] Longin F M. From value at risk to stress testing: The extreme value approach[J].Journal of Banking & Finance, 2000, 24(7)：1097-1130.

Study on CSI 300 Stock Index Futures Overnight Risk Based on CAViaR Model

JIAN Zhi-hong1,ZENG Yu-feng2,LIU Xi-teng3

(1.School of Economics HUST,Wuhan 430074,China;2.School of Economics,Fudan University,Shanghai 200433,China; 3.School of Public Economics and Administration,Shanghai University of Finance and Economics,Shanghai 200433,China)

Financial futures market is an important part of modern financial market systems in China. However, financial derivatives have natural properties of high-yield and high risk.Once a futures risk event occurs, it will cause great destructive effect to the whole financial markets.So investors have always been paying great attention to the prevention of futures' overnight risk. However, little work has been done to detect volatility characteristics and risk features of overnight return.By taking CSI300 stock index futures for sample in this paper,CAViaR model is adopted to directly calculate the common VaR of overnight return. Nevertheless, considering rare data available during optimization in extreme quantiles, the estimation results may be biased. Therefore, a new framework, which combining extreme value theory and CAViaR model, is built to estimate the extreme overnight risk and analyze the dynamic characteristic of different quantiles both in left tail and right tail.Then both Kupiec LR(likelihood ratio) test and dynamic quantile test are used to backtest the accuracy of these models.The empirical results are summarized as follows: (1) overnight return exhibits stylized facts of positive skewness, leptokurtosis and non-normal distribution. But it lacks of long-term memory property. (2) The three CAViaR models have strong predictivity power to the common overnight risk, among which the AS model performs best, while there is no significant difference between SAV model and IGARCH model. (3) After adding the extreme theory to the CAViaR model, the newly-constructed CAViaR-EVT model still can accurately depict the dynamic process of overnight risk in extreme low quantiles. Moreover, its forecast results are more reasonable than EVT model and GARCH-EVT models.Important practical and social implications are suggested. The CAViaR model and CAViaR-EVT model offer useful practical approaches to forecast futures' overnight risk. Moreover, it also provides a theoretical reference to carry out effective risk management and monitor activities for the Chinese stock index futures investors and regulators, such as position limits and margin ratio.

overnight risk；CAViaR model；CSI300 stock index futures；value at risk

2015-06-24；

2016-04-01

中央高校基本科研業務費資助項目(2016AB008)

簡介：曾裕峰(1990-)，男(漢族)，江西吉安人，復旦大學經濟學院博士研究生，研究方向：金融風險管理，E-mail：zyf_2014@126.com.

F830.91

A

1003-207(2016)09-0001-10

10.16381/j.cnki.issn1003-207x.2016.09.001