基于改進遺傳算法的自抗擾控制器優化設計

唐勇偉，趙景波，王茂勵，郝慧娟，呂曉慧

(1. 青島理工大學自動化工程學院，山東 青島 266520；2. 山東省計算中心(國家超級計算濟南中心)，山東 濟南 250014；3. 華北電力大學電氣與電子工程學院，北京 102206)

?

【海洋科技與裝備】

基于改進遺傳算法的自抗擾控制器優化設計

唐勇偉1,2，趙景波1*，王茂勵2，郝慧娟2，呂曉慧3

(1. 青島理工大學自動化工程學院，山東 青島 266520；2. 山東省計算中心(國家超級計算濟南中心)，山東 濟南 250014；3. 華北電力大學電氣與電子工程學院，北京 102206)

針對超空泡航行體受力特征及其航行時具有非線性、時滯與耦合等復雜問題，提出可根據適應度對控制參數進行自適應動態調整的改進遺傳算法。通過建立超空泡航行體縱向模型，設計專用自抗擾控制器對其進行控制，并針對控制器參數多、調節困難的問題，改進了自適應遺傳算法對其精確優化。最后通過特性仿真，驗證了基于改進的自適應算法的自抗擾控制器相比經典自抗擾控制器的優勢。仿真結果表明，該自抗擾控制器符合實際需求，具有良好的控制效果。

超空泡航行體；自抗擾控制器；改進自適應遺傳算法；解耦；參數優化

由于海水密度較大，常規水下航行體及制導武器在水中航行時所受阻力遠遠高于其在空氣中，因此航行速度慢且距離短，實際應用受到很大局限，必須尋求有效方法實現水下航行體的減阻提速。航行體在水下高速航行時通過氣體發生器產生氣化物并形成氣泡將機體覆蓋[1]，因此航行體受到的阻力顯著降低，其運動速度得到大幅提升[2]。

然而，航行體利用空泡減阻提速，沾濕面積減小，浮力作用很大程度喪失[3]，動態性能產生極大改變，致使超空泡航行體建模和控制難度大大增加[4-5]。所以，單純使用廣泛應用于常規水下航行器控制的傳統PID控制方法已不可行。自抗擾控制技術(active disturbance rejection control,ADRC)將傳統控制理論的負反饋思想與現代控制的狀態反饋部分思想結合，將系統內部及內外擾動等全部不確定因素視為系統的“總和擾動”，采用實時動態補償的擾動觀測和補償控制策略，很大程度地降低了控制器對被控系統內部結構的依賴，能夠有效提高系統的抗干擾能力，具有精確、穩定、魯棒性和適應性好等特點[6-8]。本文將自抗擾控制技術應用于超空泡航行體的控制問題，提出了可根據適應度對控制參數進行自適應動態調整的改進遺傳算法。

圖1 超空泡航行體模型縱向受力分析圖Fig.1Longitudinal force analysis diagram of supercavitation navigation vehicle model

1 超空泡航行體模型的縱向力分析

在水中運行時，航行體縱向平面的主要作用力分別為航行體質心所受到重力Fg、空化器在運行過程中受到液體流動力Fn、尾部的滑行力Fp、滑行阻力Ff和推力FT等[9]，受力相互作用，維持平衡，其縱向平面受力分析見圖1。航行體模型由柱部和錐部構成，柱部長度約為錐部的兩倍，模型中空化器、十字型鰭與實際相似[10]。

根據受力分析，可得其縱向運動模型：

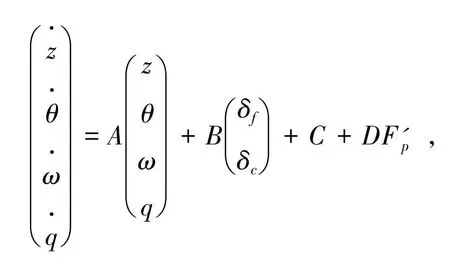
(1)

表1 航行體模型的主要參數Table 1 System parameters of the vehicle model

將上表中各參數值應用于航行體的縱向模型后，可得系統各狀態變量的系數矩陣：

(2)

2 超空泡航行體的自抗擾控制器設計

2.1 自抗擾控制器系統結構

自抗擾控制器一般包括跟蹤微分器(TD)、擴張狀態觀測器(ESO)、非線性狀態誤差反饋(NLESF)三部分[6]，三者之間的有效組合，避免了對被控系統存在的非線性進行復雜的線性化處理，從而實現對非線性系統的快速、有效、無超調地有效控制，在實際工程中應用廣泛。以二階系統為對象，自抗擾控制器的系統結構圖見圖2。

圖2 自抗擾控制器二階系統結構圖Fig.2 Second-order system structure of ADRC

其中,io(t)、O(t)、W(t)為輸入、輸出以及干擾信號；i1、i2都是輸入信號、跟蹤信號,i1是一階導數,i2是微分；S1、S2、S3是ESO估計出的三階狀態變量；e1、e2是系統的誤差量。因此，二階的自抗擾系統包含的TD為二階，ESO為三階。

2.2 自抗擾解耦控制系統

超空泡航行體系統是多輸入/輸出被控系統，各通道之間存在著耦合作用，需將多變量的控制解耦。自抗擾控制器可以將變量間的耦合當作擾動加以估計和補償，從而消除耦合對系統的影響[11]。以雙輸入/輸出系統為例說明自抗擾控制下對耦合系統的解耦原理，設被控對象為：

(3)

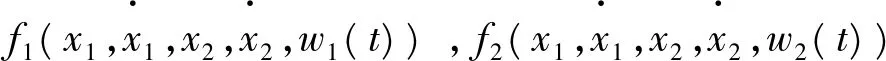
若B可逆，則

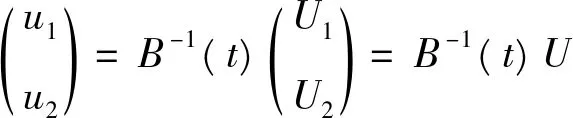
(4)

則系統等效為：

(5)

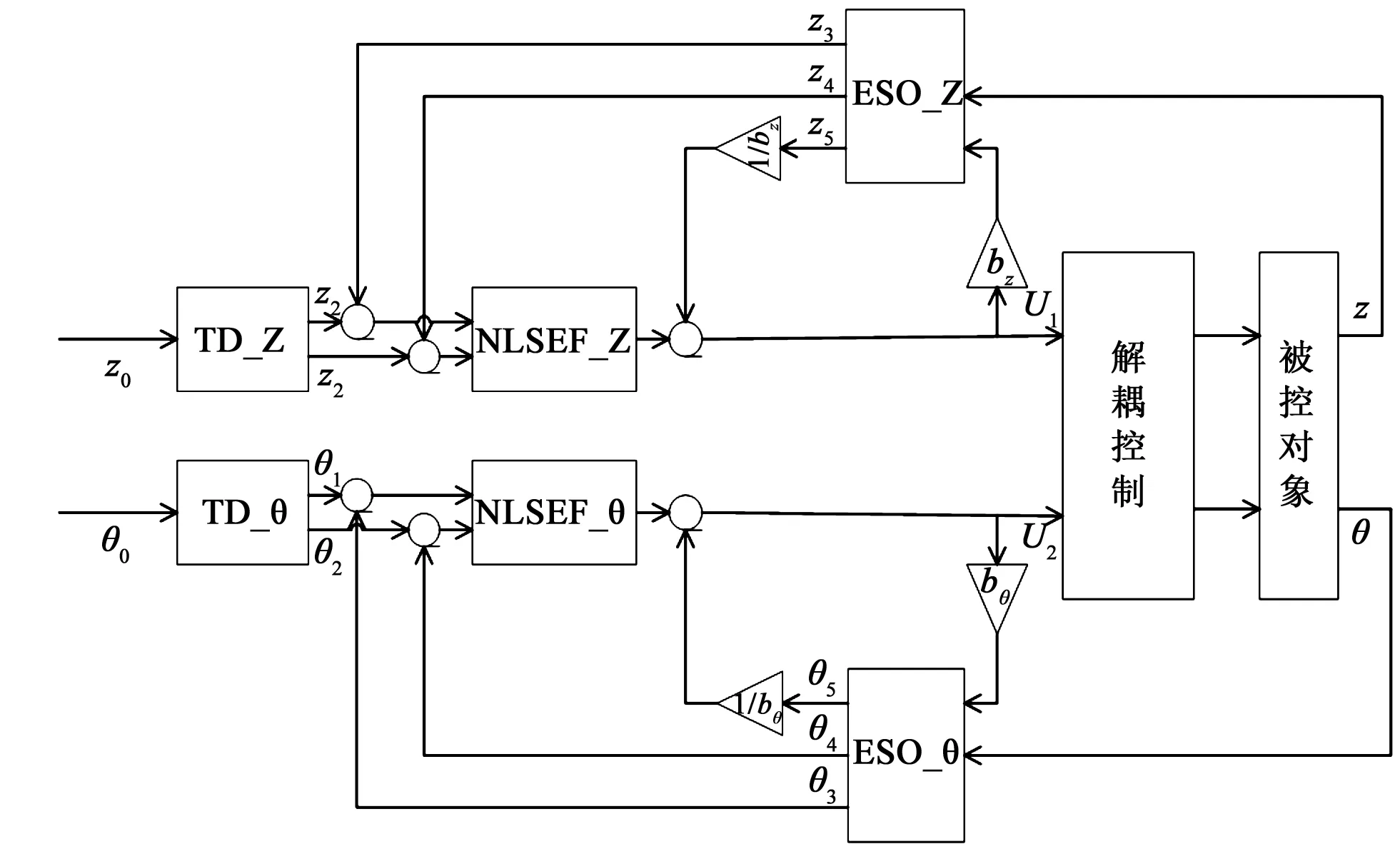
圖3 超空泡航行體自抗擾控制器設計框圖Fig.3 Supercavitation vehicle design diagram of ADRC

由等效公式(5)可以看出，只要ESO將各通道的a11和a22進行觀測實時補償，則系統就變為兩個獨立的“積分串聯型”系統。對模型補償輸出量U后，根據式(4)進行逆變換，就可獲得原系統式(3)的控制輸入u1、u2。這樣各狀態變量之間的耦合關系就不再存在，在控制時就無須對系統進行動態解耦，實現了系統的解耦控制。

2.3 超空泡航行體自抗擾控制器設計

航行體的深度、縱傾在升降舵和空化器作用下同時發生變化，所以，超空泡航行體的縱向控制系統以舵偏轉角δf和空化器偏轉角δc為控制輸入，以深度z和俯仰角θ為輸出的雙輸入雙輸出系統。本文對深度TD_Z、ESO_Z、NLSEF_Z以及縱傾TD_θ，ESO_θ、NLSEF_θ三部分的離散算法進行改進，并研究適用于超空泡航行體的自抗擾控制器，原理圖見圖3。

3 改進算法的自抗擾控制器優化設計

自抗擾控制器中r、h、α1、α2、δ等11個參數需整定[12]。本文將自抗擾控制器設計問題轉化為一種參數尋優問題，以解決目前參數調整在人工調試過程中選取調試方法及參數修改存在的很大程度的不確定性。

3.1 改進的自適應遺傳算法

遺傳算法中有選擇算法和交叉算法兩個重要內容，交叉概率PC和變異概率Pm的選擇對算法的過程和效果以及收斂性有重要影響。Srinvivas等[13]提出一種能按照適應度值調整Pc和Pm的自適應遺傳算法，這兩個參數調節公式如式(6)、式(7)。

(6)

(7)

其中，fmax、fav以及f'分別代表種群中的最大適應度值、平均適應度值和進行交叉操作的較大的適應度值。

另外，任子武等[14]提出一種采用了精英保留策略的改進自適應遺傳算法，其調節公式如式(8)、(9)，

(8)

(9)

式中，Pc1=0.9，Pc2=0.6，Pm1=0.1，Pm2=0.01。

兩種自適應遺傳算法能夠自適應調整，確保優良個體不被遺傳操作破壞，但在適應度、過程停滯等方面還存在不足。本文基于這兩種算法，改進自適應遺傳算法的Pc、Pm，使其能根據適應度對這兩個控制參數實現動態調整，其中，Pc、Pm的自適應調整的公式如(10)、(11)，

(10)

(11)

式中，fmin、f代表群體中的最小適應度值及要變異體的適應度值，Pc1>Pc2>Pc3，Pm1>Pm2>Pm3，它們的取值都在(0,1)區間內，并且在尋優過程內不斷進行調節。

改進的自適應遺傳算法會依據群體fmax、fmin、fav來判斷群體中個體自適應度值的分散程度，同時，本文采用的改進交叉概率Pc、變異概率Pm以種群為單位，依據種群個體的適應度值在種群最大、最小以及平均適應度值的范圍內自適應地進行調整變化。改進后的Pc和Pm可以滿足自適應調整，在群體最大適應度值中不會為零，相當于增大了群體中優秀個體的交叉概率和變異概率，防止這些個體演化出現停滯不前的情況。同時，將個體的適應度與當代種群的平均適應度進行比較，在進化過程中使種群的優良個體得到保留，種群較差個體的變異能力得到增強，從而使算法跳出局部最優解，增強了算法的全局搜索能力，預防早熟收斂現象，使遺傳算法的收斂性、魯棒性及優良解的多樣性得到保障和提高，實用性強。

3.2 基于改進算法的自抗擾控制器設計

本文改進自適應遺傳算法進行ADRC參數尋優，并對其優化過程的具體步驟進行設計，使復雜的參數整定簡單、精確、可靠。其參數優化過程如圖4所示。

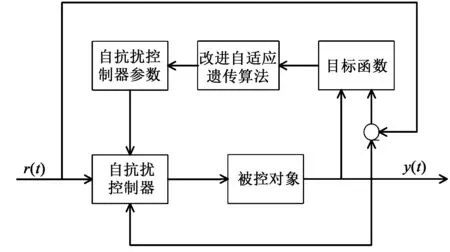
圖4 改進算法的自抗擾控制器參數優化過程圖Fig.4 Parameter optimization process diagram of ADRC of the improved algorithm

優化過程的具體步驟如下：

(1)確定適應度函數。本文將式(12)作為目標函數指標，用來評價系統動態性能、改善控制能量、控制輸入受限的性能評價，滿足控制優化設計要求。

，

(12)

其中，e(t)為系統誤差，y(t)為系統的控制輸出，σ(t)為系統的超調量。ω1，ω2，ω3為權重系數。適應度函數f=1/(J+ε)，ε是一個很小的實數。

(2)參數編碼。對二階自抗擾控制器中需要調節的參數向量t的參數進行實數編碼。

(3)產生初始種群。為了易于收斂，盡可能選取較大的群體規模值，本文選取群體規模N=20，為了使參數符合運動趨勢，在參數尋優時遺傳搜索的空間縮小，操作時間變小。

(4)計算種群適應度。根據所確定的適應度函數，計算每個個體的適應度值，對個體進行評價。

(5)個體選擇。對種群個體采用輪盤賭的方式進行選擇，選出的優良個體作為新一代的父代個體。

(6)交叉。依照式(10)設定的交叉概率Pc，采用單點交叉的方式將交叉算子用于種群，產生新的個體。

(7)變異。依照式(11)設定的變異概率Pm，以基本變異方式對交叉配對后的個體進行基因變異操作，得到新個體。

(8)終止判斷。重新評估新一代種群中染色體性能，重復(4)～(8)步操作。設置終止迭代數G=200，當滿足迭代終止條件時停止操作。結果表明，此迭代數滿足效果要求，再增加計算量和時間，改善效果變化不大。

將改進后的自適應遺傳算法與基本遺傳算法進行對比，分別對自抗擾控制器進行參數整定，仿真條件、環境參數取值與之前自適應算法仿真保持一致。在經過50代進化后，在參數尋優過程中遺傳算法與改進自適應遺傳算法的自適應值變化分別如圖5所示。

圖5 改進算法前后自適應度值變化曲線Fig.5 Fitness value changing curve before and after algorithm improvement

由圖5可以看出，使用改進后的自適應遺傳算法與之前算法相比，最終得到的種群適應度值更大，說明種群的優良性得到提高，由改進后的算法獲得的參數向量能使控制器有更好的控制性能。同時，改進算法還改善了收斂速度過快的問題。比較兩條變化曲線可知，改進的自適應遺傳算法的參數尋優效果比基本遺傳算法好。

4 仿真

將系統中存在的不確定擾動考慮在內，將超空泡速航行體的所處深度由開始的0 m調整到3 m的過程中系統狀態變化量z、θ、q、ω的變化情況如圖6所示，系統控制輸入δc、δf的變化曲線如圖7所示。

圖7 改進自抗擾控制的系統控制輸入Fig.7 System control input of improved ADRC

圖6、圖7中的虛線和實線分別為自抗擾控制器及其改進后各狀態變量的變化曲線，從圖中可以看出在系統初始狀態偏離了平衡狀態，由于自抗擾控制器的加入，航行體的深度重新達到預設位置并且能夠維持穩定，超調量很小，縱向速度、俯仰角和俯仰角速度也基本上都在這一時間到達并保持在穩定狀態。

另外，由圖6、圖7可以看出,自抗擾控制器經過優化后，各狀態變量恢復到平衡位置的調節時間縮短。位移沒有超調量的產生，縱向速度、俯仰角與俯仰角速度從初始狀態至期望狀態的波動幅度減小，而控制面存在的振蕩也得到了有效抑制。由此可知，與參數未經優化的應用于超空泡航行體控制系統的人自抗擾控制器相比，優化后的自抗擾控制器系統的魯棒性和抗擾動能力更強，參數適應能力更好，其控制性能獲得提高。

5 結論

本文根據超空泡航行體的運行特點設計了自抗擾控制器，并提供了一種新思路，即針對自抗擾控制器存在的缺點提出改進的自適應遺傳算法并對其參數進行優化。同時，利用MATLAB中搭建了超空泡航行體和自抗擾控制的仿真平臺，分析了超空泡航行體在開環狀態下各狀態變量的動態性能，驗證了自抗擾控制器對超空泡航行體優化控制的可行性。

[1]熊天紅,易文俊,吳軍基,等.水下高速航行體超空泡減阻特性數值模擬研究[J].船舶工程,2008,30(6):11-14.

[2]白濤,畢曉君.水下超空泡航行體縱向機動運動控制研究[J].哈爾濱工程大學學報,2011,32(4):445-450.

[3]張樂,張國鑫.超空泡航行體絕對穩定控制設計[J].裝備制造技術,2015(2):5-8.

[4]孫堯,趙新華,莫宏偉.水下超高速航行體的動力學建模及控制問題研究[J].哈爾濱工程大學學報,2008,29(2):144-150.

[5]KIRSCHNER I N, UHLMAN J S,PERKINS J B. Overview of highspeed supercavitating vehicle control[C]// AIAA Guidance, Navigation, and Control Conference and Exhibit. Keystone, Colorado: American Institute of Aeronautics and Astronautics Inc, 2006: 3100-3116.

[6]韓京清.自抗擾控制技術[M].北京:國防工業出版社,2008:3-9.

[7]董莉莉. 自抗擾控制技術在微機電換能器中的應用 [J]. 控制理論與應用, 2013, 30(12): 1543-1552.

[8]高志強.自抗擾控制思想探究[J].控制理論與應用,2013，30(12),1498-1510.

[9]王茂勵.超空泡航行體的數學建模與控制方法研究[D].哈爾濱:哈爾濱工程大學,2008.

[10]呂瑞,魏英杰,于開平,等.超空泡航行體的增益自適應全程滑?？刂破髟O計[J].振動與沖擊,2011,30(3):34-37.

[11]朱必剛,紀志成.基于永磁同步風力發電系統的自抗擾控制[J].江南大學學報(自然科學版),2011,10(4):385-390.

[12]王東振,文新委,宋剛.自抗擾控制器參數整定的一種新方法[J].黑龍江電力,2012,34(1):71-73.

[13]SRINIVASM, PATNAILK L M. Adaptive probabilities of crossover and mutation in genetic algorithms[J]. IEEE Transaction on System, Man and Cybernetics,1994,24(4):656-667.

[14]任子武,傘冶.自適應遺傳算法的改進及在系統辨識中應用研究[J].系統仿真學報,2006,18(1):41-43.

Improved genetic algorithm based optimization design of active disturbance rejection controller

TANG Yong-wei1,2, ZHAO Jing-bo1*, WANG Mao-li2,HAO Hui-juan2, Lü Xiao-hui3

(1. School of Automation Engineering, Qingdao University of Technology, Qingdao 266520, China；2. Shandong Computer Science Center (National Supercomputer Center in Jinan), Jinan 250014, China;3. School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China)

∶We present an improved genetic algorithm that can adaptively adjust control parameters based on fitness degree for the force characteristics of supercavitation navigation body and such complicated issues as nonlinearity, time lag and coupling. We construct longitudinal model of supercavitation navigation body, which is controlled by a specific active disturbance rejection controller (ADRC). We further improve adaptive genetic algorithm to precisely optimize it for such issues as mass controller parameters and difficult adjustment. We eventually verify the advantage of the improved ADRC over classical ADRC through simulation. Simulation results show that the improved ADRC satisfies practical requirements and has better control effect.

∶supercavitation navigation body; active disturbance rejection controller; improved adaptive genetic algorithm; decoupling; parameter optimization

10.3976/j.issn.1002-4026.2016.05.001

2016-05-12

國家自然科學基金項目(51475251)；山東省自然科學基金(ZR2013FM014；ZR2015FQ015；ZR2014EEM024)； 山東省自主創新及成果轉化專項(2014CGZH0806)

唐勇偉(1991—)，男，碩士，研究方向為控制理論與智能控制。

*通信作者。Email：zhaojingbobg@163.com

TP29

A