能量法分析重力和點電荷雙場聯合作用下的微幅擺動
陳奎孚 陳 雷 蔡 春
(1中國農業大學理學院,北京 100083; 2北京聯合大學應用文理學院,北京 100191)
?

能量法分析重力和點電荷雙場聯合作用下的微幅擺動
陳奎孚1陳 雷1蔡 春2
(1中國農業大學理學院,北京 100083;2北京聯合大學應用文理學院,北京 100191)
單擺是經典的教學案例.為了豐富教學材料,文章分析了點電荷場和重力場聯合作用下的擺動.采用了適合于單自由度的自然坐標系描述系統,使用了適合于復雜力學的能量法建立動力學方程.針對固定點電荷處于擺懸掛點垂線的特殊情形,通過理論分析界定了擺球最低、倒立和傾斜等平衡位置的參數范圍.
擺;點電荷;振動;能量法;自然坐標系
單擺在中學物理和大學物理中都是一個典型物理教學案例[1].最簡單的模型是沒有重量且沒有彈性的細繩懸掛大小不計的擺球在重力場中微幅擺動.為了豐富教學內容和增強學習興趣,很多教學材料又對最簡單的模型進行了拓展,如加速懸掛點、放置斜面、增加均勻電場力等.很多拓展模型的求解只需對基本模型的解進行簡單修正就可以了,這是因為在這些例題中,拓展的作用僅相當于增加了一個均勻的力場.
點電荷場是物理教學的基本內容,但是由于場強的不均勻性,將它與重力場聯合作用于擺所引起的物理現象就復雜了,僅就其平衡位置而言,除了常規的擺球最低情形外,還有倒立和傾斜等情形.文獻[2]僅就擺球最低這一常規平衡位置情形進行了詳盡的研究,本文則利用能量法[3]進行更為一般的討論,并就固定點電荷處于擺懸掛點垂線上的特例,給出所有穩定平衡位置的參數取值范圍.
1 能量法[3]
擺的自由度只有一個,質點的運動軌跡是已知的,所以可選擇沿質點軌跡的弧坐標s為廣義坐標.相應地,質點動能Ek可簡潔地表示為
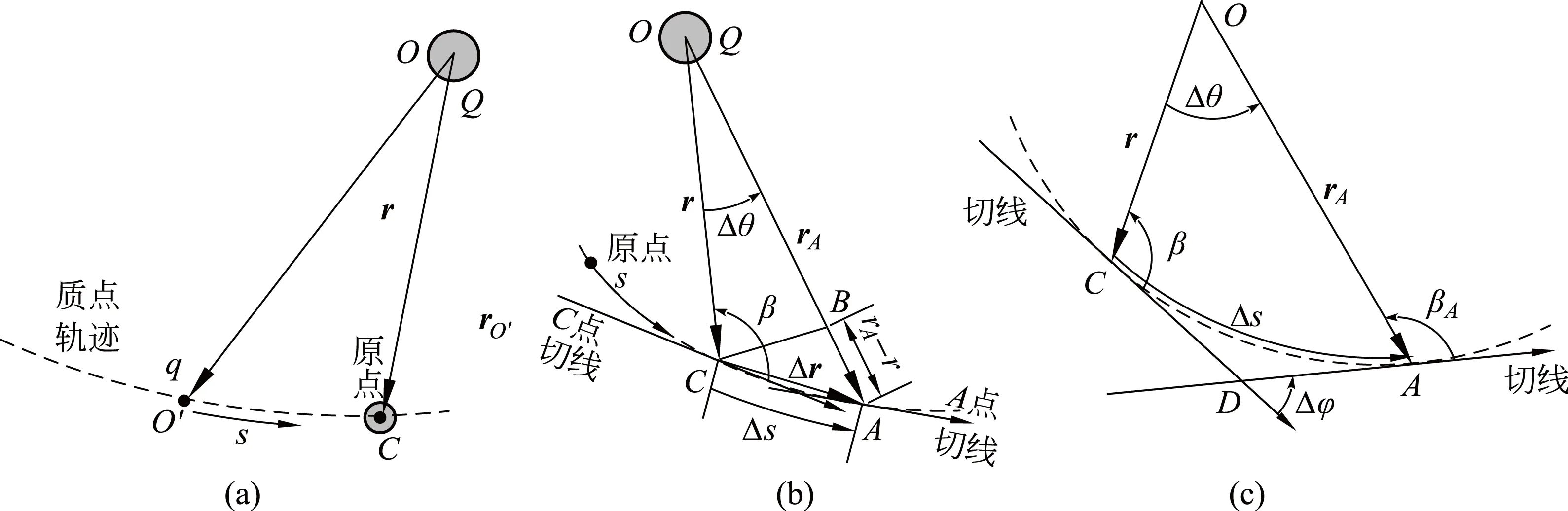
圖1 兩個點電荷相互作用的勢能分析
(1)
記系統勢能為Ep,它等于各勢能的代數累加.勢能是位置的函數,質點的位置由其弧坐標s唯一確定,所以Ep是s的函數Ep(s).
對無阻尼情形,動能與勢能之和總能量E守恒,即不隨時間而變.數學語言表示為
(2)
兩邊對時間求導有
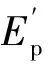
(3)
假定系統能夠發生微幅簡諧振動,記系統平衡位置s=sb.對于微幅振動,可把Ep(s)展開成s-sb的泰勒級數,即
(4)
代入式(3)得到
(5)
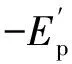
(6)
如果在分析一開始就找到平衡位置,并且設平衡位置的sb=0,則式(6)變成如下簡潔的形式
(7)
式(6)為線性微幅振動微分方程.對應物理系統的固有頻率為
(8)
或振動固有周期為
(9)
從式(6)(或式(8))可以看出,線性微幅振動分析的關鍵是找到E″p(sb).與彈簧振子的微分方程相比,式(7)的E″p(0)相當于彈簧的勁度系數.穩定平衡則要求E″p(sb)>0;而E″p(sb)<0則為不穩定平衡(系統無法發生“圍繞”不穩定平衡位置的往復運動);E″p(sb)=0為臨界情形,系統能否發生圍繞s=sb振動,需要檢查更高級導數的正負.
2 兩個點電荷相互作用的勢能分析
運用式(6)的關鍵是寫系統勢能,先看圖1(a)所示兩個點電荷相互作用的勢能,圖中O處點電荷固定(Q),移動點電荷q沿軌跡運動.選擇O′為零勢能點,則電荷A的電勢能為
(10)
式中,k=9×109N·m2/C2為靜電力常量.將Ee(s)對s求導有
(11)
(12)
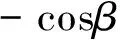
(13)
將式(13)代入式(12)得到
(14)
將式(14)代入式(11)得到
(15)
對式(15)再次求導有
(16)
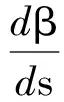
(17)

從該式解出βA-β=Δθ-Δφ,代入式(17)有
(18)
考察圖1(b)可知,Δssinβ≈BC≈rΔθ,因此式(18)中的
(19)
圖1中的固定電荷和質點軌跡的曲率中心在軌跡的同側.對于二者在曲線兩側的情形,同樣可證式(19)仍然成立.將式(14),式(18),式(19)代入式(16)得到
(20)
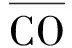
3 電荷場與重力場聯合作用
考查圖2所示的聯合作用情形.直角坐標系原點過單擺的懸掛點H.固定點電荷Q位于 O(a,b).擺長l, 擺球是質量為m質點,帶有電荷q.自然坐標原點取為擺球的最低點,正方向如圖2所示.重力勢能和電勢能的零點均選擇自然坐標原點.
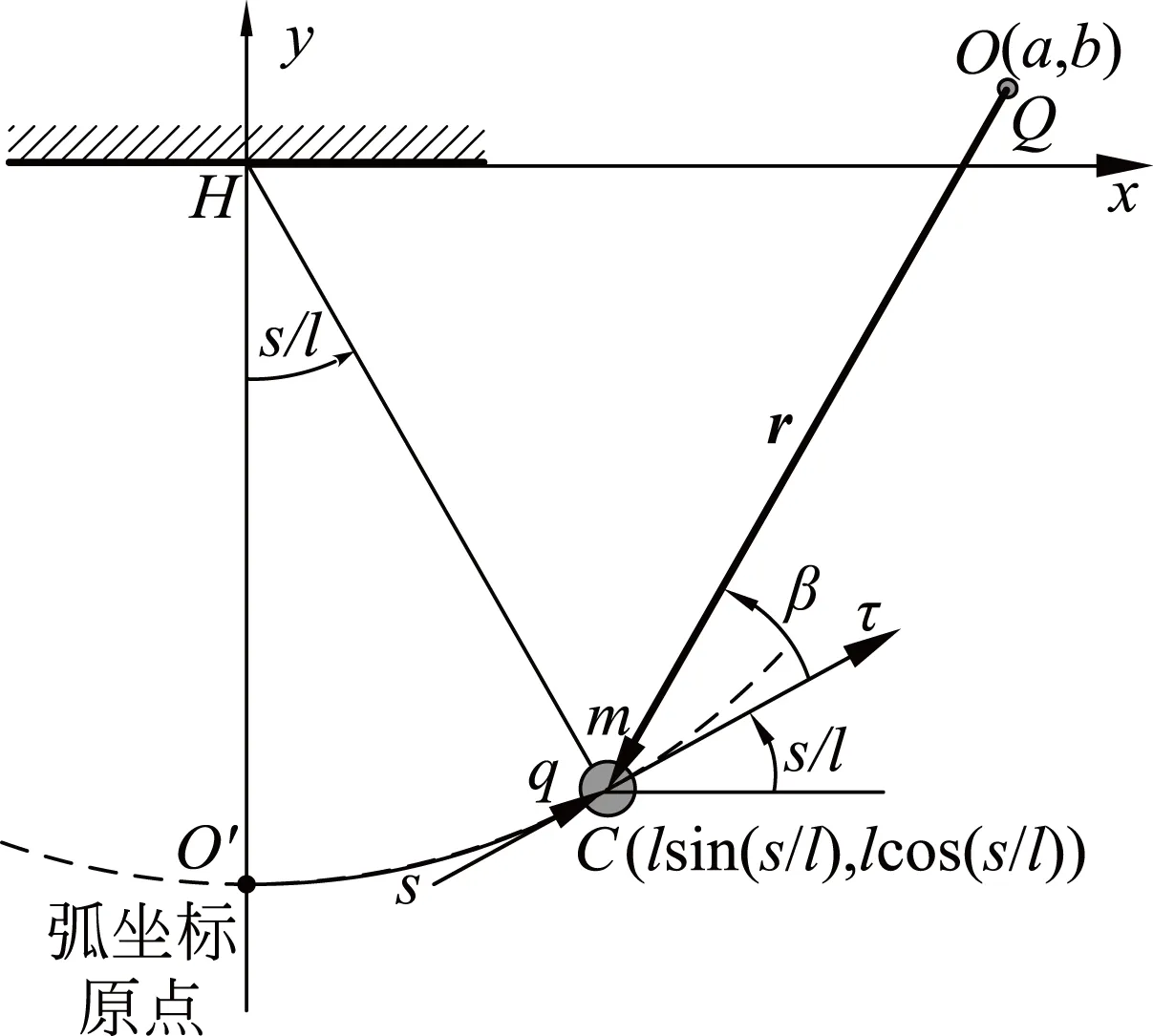
圖2 點電荷場與重力場聯合作用
重力勢能為
它對弧長的一階和二階導數分別為
系統的勢能為
(21)
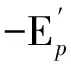
(22)
其中
(23)
(24)
式(22),式(23)和式(24)看起來很復雜,但它們只是關于單變量sb的方程.一旦a,b,l,q,Q給定,就可以通過數值方法確定出sb.確定出sb后,可用它作新自然坐標的原點,就得到式(7)那樣微幅簡諧振動方程了.
等效剛度E″p(sb)則為
(25)
固有頻率和簡諧振動周期分別按式(7)和式(8)確定.
為了便于分析,引入如下無量綱參數
則式(22)~ (25)可分別寫成
(26)
(27)
(28)
(29)
4 特例考察
本文只考察固定電荷Q位于y軸的特殊情形,相應的a=0.式(28)的余弦變成
(30)
代入式(26)得到
(31)
解方程(31)得到平衡位置
(32)
(33)
(34)
4.1 常規穩定平衡
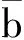
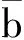
E″p(θb)>0要求
(35)
此時s=sb=0為穩定平衡位置,對應的振動周期為
(36)
若采用與文獻[1]相同的符號,則式(36)就是該文的式(2).
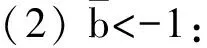
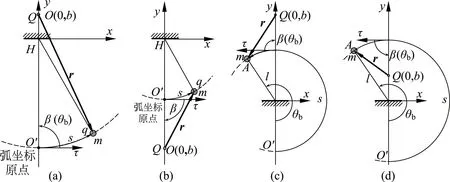
圖3 平衡位置類型分析
(37)
穩定平衡E″p(θb)的要求為
(38)
當式(39)得到滿足時,系統的固有周期為
(39)
若采用與文獻(1)相同的符號,則式(39)就是該文的式(4).
4.2 倒立穩定平衡
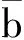
(40)
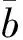
(41)
4.3 傾斜穩定平衡
式(33)的右邊必須大于零,所以有μ<0.該條件得到滿足后,從式(34)可解得
(42)
若式(42)的解存在,則正負各有一個.但是解的存在還要補充其他條件.根據三角函數的性質有
(43)
進一步化簡得到
(44)
(45)
穩定平衡E″p(θb)的要求為
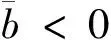
(46)
相應地,式(44)的關系也就能更進一步明確為
(47)
這類穩定平衡是靠位于擺懸掛點下方的同性電荷的斥力來維持的.
三類穩定平衡的參數范圍如圖4所示.由圖可知傾斜平衡和常規平衡是互斥的,即同一組參數不可能既有常規平衡,又有傾斜平衡.同樣倒立平衡和傾斜平衡也是互斥的.但是常規平衡和倒立平衡卻是可以同時存在的.

圖4 三類穩定平衡的參數范圍
5 微幅振動討論
由式(6)只要保證E″p(θb)>0,系統就會圍繞平衡位置發生微幅簡諧振動,而不管點電荷位于何處,只是當點電荷處于擺的懸掛點的垂線上時,分析過程比較簡單一點,正如第4節所述.當然點電荷不在擺的懸掛點的垂線上,那么平衡的θb一般不再為零,但是仍然可以通過式(26)~(29)來確定,并且是繞θb的簡諧振動.因此對“點電荷場與重力場疊加時的方向關系是帶電單擺保持簡諧運動的首要因素”的說法不能茍同.
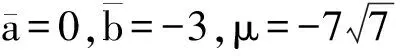
是不是所有微幅振動都是簡諧的呢?從式(6)來看,這似乎是肯定的,但是E″p(sb)=0則為例外情況,圖5(a)就是這樣的物理模型.圖中振動系統位于光滑的水平面,振動沿彈簧軸線的垂直方向運動,過平衡位置彈簧無伸長.這個模型因E″p(sb)=0,所發生振動即使很微小,也不能用簡諧振動來近似.
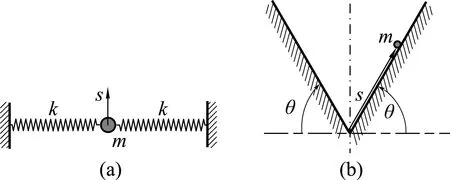
圖5 非簡諧微幅振動
式(6)的操作默認了勢能函數二階可微.但是也有Ep(s)的二階導數不存在的模型,比如圖5(b)所示的在對稱光滑V形槽內質點的運動,其重力勢能Ep(s)=|s|sinθ)就沒有二階導數.雖然質點可以在V形槽內往復運動,但即使幅度再小,也不符合簡諧規律.
6 結語
本文研究了在重力場和點電荷場共同作用下的擺.由于系統為單自由度系統,擺球的軌跡已知,所以采用了自然法描述系統.又因為所研究的系統相對復雜,故采用能量法建立振動微分方程,
它的操作過程比受力分析法要簡潔一些.
因為采用的是自然坐標系,所以本文推導了矢徑長度對自然坐標的導數和軌跡到矢徑的角度對自然坐標的導數.這兩個導數是進行相關研究的數學基礎.
針對點電荷位于擺懸掛點鉛垂線上的情形,經由理論分析得出它具有常規、倒立和傾斜三類穩定的平衡位置.給出了3類穩定平衡的參數范圍.
對微幅振動和簡諧振動的概念進行了辨析.
[1] 梁紹榮,劉昌華,盛正華.普通物理學[M].北京:高等教育出版社,1999:233-235.
[2] 唐安琪,陳鋼,朱國斌,等.點電荷場中的重力單擺及簡諧振動[J].物理與工程,2015,25(3):79-83.TangAQ,ChenG,ZhuGB,etal.GravityPendulumandHarmonicVibrationintheFieldofPointCharge[J].PhysicsandEngineering, 2015, 25(3): 79-83.
[3] 陳奎孚.機械振動基礎[M].北京:中國農業大學出版社,2011:29-31.
■
ON THE MICRO-AMPLITUDE VIBRATION OF A PENDULUM IN THE SIMULTANEOUS FIELD OF THE GRAVITY AND POINT CHARGE BY THE ENERGY METHOD
Chen Kuifu1Chen Lei1Cai Chun2
(1College of Science, China Agricultural University, Beijing 100083;2College of Arts and Science, Beijing Union University, Beijing 100191)
The simple pendulum is a typical teaching case. To enrich teaching materials, we studied the micro-amplitude pendulum vibration caused by the simultaneous point charge and gravity fields. The system is described by the natural coordinate system, which is apt to the single-degree-of-freedom case investigated here. The dynamics equation is evolved from the energy method, which is more concise than the free-body-diagram method for the complex system in this study. After a general analysis, we focus on a particular case wherein the point charge is at the vertical line passing through the pendulum suspension point. Theoretical analysis indicates that this particular case is characterized with three types of stable balance. The three types are the ordinary, the inverted and the oblique distinguished by the pendulum rope’s inclination. Their parametric domains are delimited.
pendulum; point charge; vibration; energy method; natural coordinate system
2015-09-08;
2016-03-03
北京市屬高等學校高層次人才引進與培養計劃項目(CIT&TCD201404080).
陳雷,男,碩士研究生,力學專業.
蔡春,女,教授,主要從事數學科研和教學工作.caichun@buu.edu.cn
陳奎孚,陳雷,蔡春. 能量法分析重力和點電荷雙場聯合作用下的微幅擺動[J]. 物理與工程,2016,26(6):25-30.

