巧用函數思想,妙解數學問題
江蘇省鹽城中學 何 瑩
巧用函數思想,妙解數學問題
江蘇省鹽城中學 何 瑩
函數思想是高中數學解題中至關重要的思想方法,它涉及知識點多,覆蓋面廣,綜合應用強,解法靈活多樣,對于培養學生思維深刻性、靈活性和創造性,提升學生思維品質,培養學生良好數學素養有著積極的作用。在高中數學教學中,教師要注意有效滲透函數思想,巧妙地運用函數定義、性質、圖象、值域等函數思想載體去分析、轉化和解決問題,從而使問題得以快速、巧妙、準確、有效地解決。對此,筆者從自身教學實踐出發,就如何在高中數學教學中引導學生巧用函數思想妙解數學問題略談了如下看法,以供參考。
一、利用函數定義,有效解決數學問題
在高中數學中,函數的基本定義是:設A、B是非空數集,若根據某個確定的對應關系f,使對于集合A中的任意一個數x,在集合B中都有唯一確定的數f(x)和它對應,那么就稱f:A→B為從集合A到集合B的一個函數,記作y=f(x),x∈A。其中x叫做自變量,x的取值范圍A叫做函數的定義域;與x的值相對應的y值叫做函數值,函數值的集合{f(x)|x∈A}叫做函數的值域。
函數定義是學生學習和掌握函數知識的重要基礎。靈活運用函數定義解決數學問題,既可以深化學生對函數概念的理解,又可以提高學生應用函數定義解題的意識,發展學生的思維能力。許多學生在解函數問題時感覺束手無策,無從下手,究其主要原因是學生對函數定義理解不透徹,把握不當,因此在平時教學中,教師要注意強化函數概念,增強學生解題能力。
例1 若f(x)與g(x)都是定義在R上的函數,且方程x-f[g(x)]=0有實數解,則g[f(x)]不可能為()
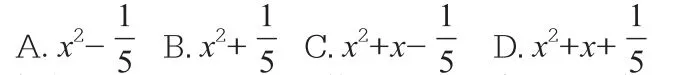
解析:此題乍看之下學生可能無從下手,但若能結合函數定義,則可使問題豁然開朗。方程x-f[g(x)]=0有實數解,設解為a,將其代入得a-f[g(a)]=0,把方程看成函數,這樣a-f[g(a)]=0可理解成在g(x)定義域中存在元素a經過映射g,設對應的象為b,b經過映射f后,在f(x)的值域中存在a與之相對應。這樣對于g[f(x)]而言,函數定義可知存在b,使得g[f(b)]=b成立,即方程g[f(x)]=x有解,將上述選項中的答案逐一代入進行驗證,可知g[f(x)]不可能為x2+x+,故應選D。
例2 已知集合M={a,b,c},N={-2,0,2},求建立從M到N且滿足f(a)+f(b)+f(c)=0的函數f的個數。
解析:許多學生在解答本題時往往束手無策,不知如何下手。事實上,本題的解題突破口是正確理解f(a)+f(b)+f(c)=0這一函數。根據函數的基本定義不難發現,f(a),f(b),f(c)三個函數均是屬于集合N中的元素,因而此題可以轉化為從N中可任意取3個元素(可重復)滿足f(a)+f(b)+f(c)=0這一已知條件。由于每個式子對應著一個函數關系,又由于f(a)+f(b)+f(c)=0的表達式僅有0+0+0=0或-2+0+2=0,因此,滿足題意要求的函數f的個數為:。
點評:在解某些數學問題的過程中,靈活巧妙地運用函數定義解題,往往可以收到事半功倍的效果。
二、把握函數性質,靈活解決數學問題
函數的基本性質主要包括了函數的奇偶性、單調性、周期性、對稱性等方面,函數性質是歷年高考考查的熱點和重點內容。在解某些問題時,若能善于挖掘問題的隱含條件,有效構造函數,靈活巧妙地運用函數性質,往往可以達到化繁為簡,化難為易的目的,從而使問題迎刃而解。因此,在平時函數教學中,教師要注意引導學生正確理解函數性質,把握好函數內涵的外延和本質特征,為數學解題奠定良好的基礎。
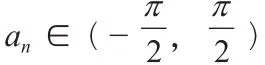
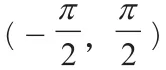

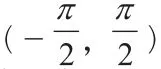
點評:本題主要考查了學生對函數奇偶性、單調性以及等差數列性質的掌握情況和學生的綜合應用能力。
三、結合函數圖象,輕松解決數學問題
函數圖象是函數的基本表達形式之一,是研究和表述函數的重要工具,它將函數的變化趨勢直觀化,以圖形的形式直觀地展現函數的性質特征,借助函數圖象的直觀性解題,可以簡化解題過程,使問題得以輕松獲解。
例4 若不等式x2+ax+1≥0對于一切x∈(0,]成立,則a的最小值是()

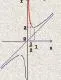
點評:巧妙地結合函數圖象分析和解決數學問題,往往可以使一些看似復雜的問題變得簡單化,從而迅速找到問題的突破口,巧妙求解。
總之,函數思想貫穿于整個高中數學教學中,具有廣泛性、多樣性、靈活性、創造性等特點。在平時教學中,教師應重視函數思想的有效滲透和靈活運用,引導學生充分挖掘數學問題中隱含的函數思想,學會巧用函數概念、性質、圖象來分析、轉化和解決問題,從而幫助學生掌握函數思想,提升學生思維品質,增強學生數學解題能力。

