談小學數學創新思維能力的培養
董洪端
現代教育呼喚創造性人才,如何有效培養學生的創新意識、創新精神,發展其創新能力和實踐能力,已經成為教育工作者研究的重要課題。下面根據自身教學經驗,就小學數學學科教學中如何營造創新學習氛圍,鼓勵學生大膽探索,培養學生創新能力和實踐能力,教學過程民主化等問題談一些做法和體會。
一、提高數學能力,培養創新能力
數學教學的重要任務之一就是提高學生的數學能力。對小學生而言,數學能力就是學習數學(再造性)的能力。即在數學學習過程中迅速而成功地掌握知識和技能的能力。主要表現為計算能力、邏輯思維能力和空間想象能力等三大方面。克魯切茨基認為,學習數學的能力是創造性數學能力的一種表現:“對數學的徹底的、獨立的和創造性的學習,是發展創造性數學活動能力的先決條件——是對那些包含新的和社會意義內容的問題,獨立地列出公式并加以解答的先決條件”。在這里,克魯切茨基通過數學活動中解決具有社會意義的實際問題,把學習數學能力與“創造性”數學能力(指在數學科學活動中的能力,能產生具有社會價值的新成果或新成就)聯系起來,展示了兩種能力的可轉化關系。因此,在數學教學中要提高學生學習數學的能力,并向“創造性”數學能力轉化,就必須注重數學活動教學,使學生在數學學習中形成和發展學習數學能力,并力爭參與社會實踐,解決具有社會意義內容的實際問題,促使其創新能力形成。
二、營造民主氛圍,誘發創新意識
人際關系的平等,為人處世的民主化作風是當代公民必須具有的素質之一。在教學工作中,課堂教學要營造民主、平等的氛圍,一個重要方面是平等的師生關系。“親其師而信其道”。師生情感融洽能使學生敢想、敢問、敢說,從而誘發創新意識。我的做法是:學習中互助合作,對關鍵性問題展開討論,人人都有發言的機會,講錯了也不要緊,對學生的作業展開自評、互評,鼓勵學生勇敢發言、積極爭論、動手操作。如教學三角形具有穩定性和四邊形容易變形的特性時,準備了一大把從樹上剪下來的枝條走進教室,所有學生一齊望著我。我發給每個學生一根枝條、一根線,并說:你們把手中的枝條折合成一個封閉圖形,不超過四條邊,看誰圍成的圖形最具有穩定性,誰將來就會成為建筑工程師。如果誰圍成的圖易變形,他將來便專門設計拉閘門。學生都忙著動手,圍成了長方形、正方形、平行四邊形、三角形……然后各自拉自己的圖形,結果得知什么形狀易變形,什么形狀不變形,各人為自己的創造爭論不已,高興不巳。雖是一個開玩笑的許諾,同學們卻都帶著美麗的憧憬產生濃濃興趣,學得生動、活潑、主動,由教育的“被動角色”躍為“主動角色”,學生學習興趣被激發了。
教購物付款找錢問題的應用題時,我說:這里有三支鋼筆,15元錢,上來兩個同學表演,一個當售貨員,一個當顧客,顧客要算出三支鋼筆的錢,每支鋼筆3.5元,然后交給售貨員15元,售貨員負責找回多少錢。兩個人都要用禮貌用語,看誰表演得好,我和全班同學當評委。結果兩人都完成了自己的任務,并用上了“麻煩”、“謝謝”、“歡迎您再來”等禮貌用語。表演的同學非常認真,下面的同學也都聚精會神。這樣,學生就把枯燥的兩步計算應用題化難為易,變單調為多彩。通過形象和具體的情節給人以快樂,學生由“扮演角色”到“進入角色”,完成了學習任務。
教學時間“年、月、日”時,我要學生說出生的那年是閏年還是平年?如果是2月生的那月是28天,還是29天?結果學生忙著動筆、動腦,個個爭著舉手發言。我常常把學習內容跟學生生活實際聯系起來,發揚民主,學生成了學習的主人,課堂氣氛熱烈,促使“創新”思想的幼芽在兒童心靈中萌發。
其次,教師批改作業時不僅要留意學生解題的正誤,更要善于發現學生創造性思想和閃光點,適時以精妙之語激發學生思維浪花,啟發學生拓展思路,發揮潛能。如解答工程題,批改作業的時候,我在做對的旁邊寫簡潔的評語:“如果工作總量變了,你會解嗎?”“如果具體工作總量不知道,你又會解嗎?”通過評語啟發,學生茅塞頓開,相繼列出幾種正確而簡捷的算式。這時我又對最簡單的做法寫上“優+,有創造性”的評語,學生看了很高興,還對前幾種方法進行了比較分析,找出了規律。這樣,學生的創新精神得到了肯定,進一步激發了創造性學習動力。
三、掌握解題策略,激活創新思維
解決問題的能力是數學能力的核心。數學課中的附加題訓練應著重讓學生開闊思路,掌握思考問題的方法、策略,從而激活學生創新思維。
(一)正面行不通則從反面下手
如下圖中的小方格都是邊長為1厘米的小正方形,求陰影部分的面積。
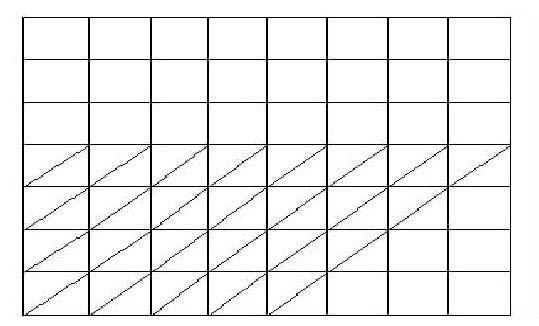
分析:由于陰影部分是沒有學過的梯形,根據已知條件無法直接求出它的面積。從反面入手考慮,就會發現整個圖形是長方形。空白的圖形為一個長方形和直角三角形,它們的面積易求,于是得解。
(二)滲透代數方法
例如:一塊長方形鐵皮,長是50cm,若在它的一端切去一塊最大的正方形,剩下的長方形周長是多少厘米?分析:如果用算術方法解,似乎缺少條件,不能解出。可用字母表示長方形的長和寬,看看題目反映的數量關系。
設原長方形的長為a,寬為b,那么剩下的長方形周長是(a-b)x2+bx2=ax2,即剩下的長方形的周長是:50X2=100(厘米)。
上面所舉的解題方法有一定的通用性,就是說,學生解另外一些數學問題時是有幫助的。所有這些方法都可以說是“策略”。實踐證明,以解題策略的探討為載體,可以培養學生的創造性思維,提高學生數學能力。
數學過程實質上是將課本數學思維活動通過教師的中介,轉化成學生思維的過程,讓學生主動經歷探索結論的過程,不僅品嘗到思維的結果,還欣賞到思維過程的無限風光,感到他們的一次發現竟與數學家不謀而合,這樣學習數學怎么不讓人流連忘返呢?
教學實踐使我深深地體會到,只要教師創造性地挖掘、研究和使用教材中的創造性因素,創造性地教,就能喚起學生創造性地學,教與學就能碰撞出創造的火花,學生就能萌發創新意識,教育就能培養出國家需要的創新型人才。

