基于3-UPS/RRR的并聯踝關節康復機構及其性能分析

李劍鋒 徐成輝 陶春靜 季潤 李世才 張兆晶

基于3-UPS/RRR的并聯踝關節康復機構及其性能分析

李劍鋒1,2徐成輝1,2陶春靜3季潤3李世才1,2張兆晶1,2

基于踝關節的生理解剖結構和運動特性分析,提出了一種適用于踝關節康復的3自由度3-UPS/RRR并聯機構.該機構采用三個主動支鏈傾斜布置避開了機構的奇異位形,能滿足踝關節康復運動需要,同時約束支鏈和動平臺的設計使機構的轉動中心與患者的踝關節轉動中心重合.應用解析法得到了機構的位置反解,建立了速度雅可比矩陣和靜力雅可比矩陣,求解了機構的工作空間.基于雅可比矩陣,仿真分析了機構的運動學性能和靜力學性能.結果表明在規定的工作空間內機構具有良好的可操作性、運動靈活性、剛度特性和力矩傳遞性能.最后運用牛頓-歐拉法建立了機構的逆動力學方程,得到了驅動力、約束力與運動參數的關系,并給出了仿真實例.

踝關節康復,并聯機構,約束支鏈,力矩傳遞性能,牛頓-歐拉法

DOI10.16383/j.aas.2016.c160144

踝關節是人體下肢的三大關節之一,是人體運動的重要樞紐和承重關節.在日常生活中,踝關節直接參與站立、跨步、跳躍等動作,并吸收來自地面的沖擊,起到保護關節的作用[1].但無法回避的是,人類是由四足行走的人猿進化而來的,所以在進化成兩足直立行走后,人類的足部關節存在著先天的缺陷.這種先天的缺陷使得人類的踝關節成為最容易受到損傷的人體關節之一.若踝關節損傷未得到及時、正確的治療,受損傷的本體感覺系統會加重踝關節的不穩定狀態,導致再次損傷的發生幾率上升,甚至引起其他關節損傷,出現不良連鎖反應[2?3].因此,踝關節損傷后,除了配合藥物治療,還應該進行康復訓練,以提高康復效率,傳統的康復訓練由醫務人員一對一進行,工作量大,效率比較低,所以隨著康復機構的快速發展,相應的踝關節康復機構逐漸進入研究人員視野.踝關節康復機構的應用不僅可以提高康復訓練工作效率,減輕醫務人員的工作量,還有利于對康復效果進行評估,以此制定相應階段的訓練內容,具有良好的使用價值和應用前景.

目前,國內外有關踝關節康復機構的研究已取得了一定的成果.文獻[4?5]中基于Stewart平臺研制出六自由度的Rutgers踝關節康復系統,采用虛擬現實技術可實現人機交互,醫生還可根據存儲的康復數據指導訓練,但該系統結構復雜,成本較高.文獻[6]提出了由三條支鏈、一根中心支撐桿和上下平臺組成的兩轉動自由度的踝關節康復機器人,采用冗余驅動來消除機構的奇異性,僅能完成踝關節背伸/跖屈和內翻/外翻康復運動.文獻[7?8]分別討論了3-RSS/S和3-SPS/S康復機構,這兩種機構的共同點是采用中央約束球鉸設計,使機構只有三個相互正交的轉動自由度,滿足踝關節康復運動需要,但是機構的轉動中心與踝關節轉動中心不重合,康復過程中需要小腿配合隨動,一旦協調不一致,可能會對踝關節造成二次傷害.文獻[9]采用三個轉動軸線正交的轉動副等效約束球鉸,提出了一種3-RUS/RRR冗余驅動踝關節康復機構,使機構的轉動中心與踝關節的轉動中心重合,且機構具有良好的運動性能,但是機構采用冗余驅動,支鏈間易引起干涉.最后文獻[10]提出了4-UP(Pe)S/S踝關節康復機構,其機構系統由簡化為球副的踝關節和機械本體共同構成,能夠實現以踝關節為轉動中心的康復訓練,但是需要踝關節承受限制三個移動產生的作用力,對康復效果不利.

綜上所述,現有踝關節康復機構各有優點,但也存在不同程度的問題:機構自由度冗余或不足;機構轉動中心與踝關節轉動中心不重合;結構復雜、成本高等.所以設計出具有三維轉動自由度且機構轉動中心和踝關節轉動中心重合,結構簡單、使用方便的機構構型,是研究踝關節康復機構的重點.基于上述分析,本文提出了一種用于踝關節康復運動的3-UPS/RRR并聯機構,該機構有三個方向的轉動自由度,機構轉動中心與踝關節轉動中心重合.

1 踝關節運動分析和機構簡介

1.1 踝關節的運動分析

踝關節由小腿的脛骨和腓骨的遠端與腳上的距骨組成[11].踝關節日常運動的三種最基本的方式包括:背伸/跖屈、內翻/外翻和內收/外展,由于性別、年齡、身體狀況的不同,踝關節的運動范圍不盡相同.經過查閱資料[12]匯總得到,正常情況下踝關節的運動模式及其運動范圍,如圖1所示.

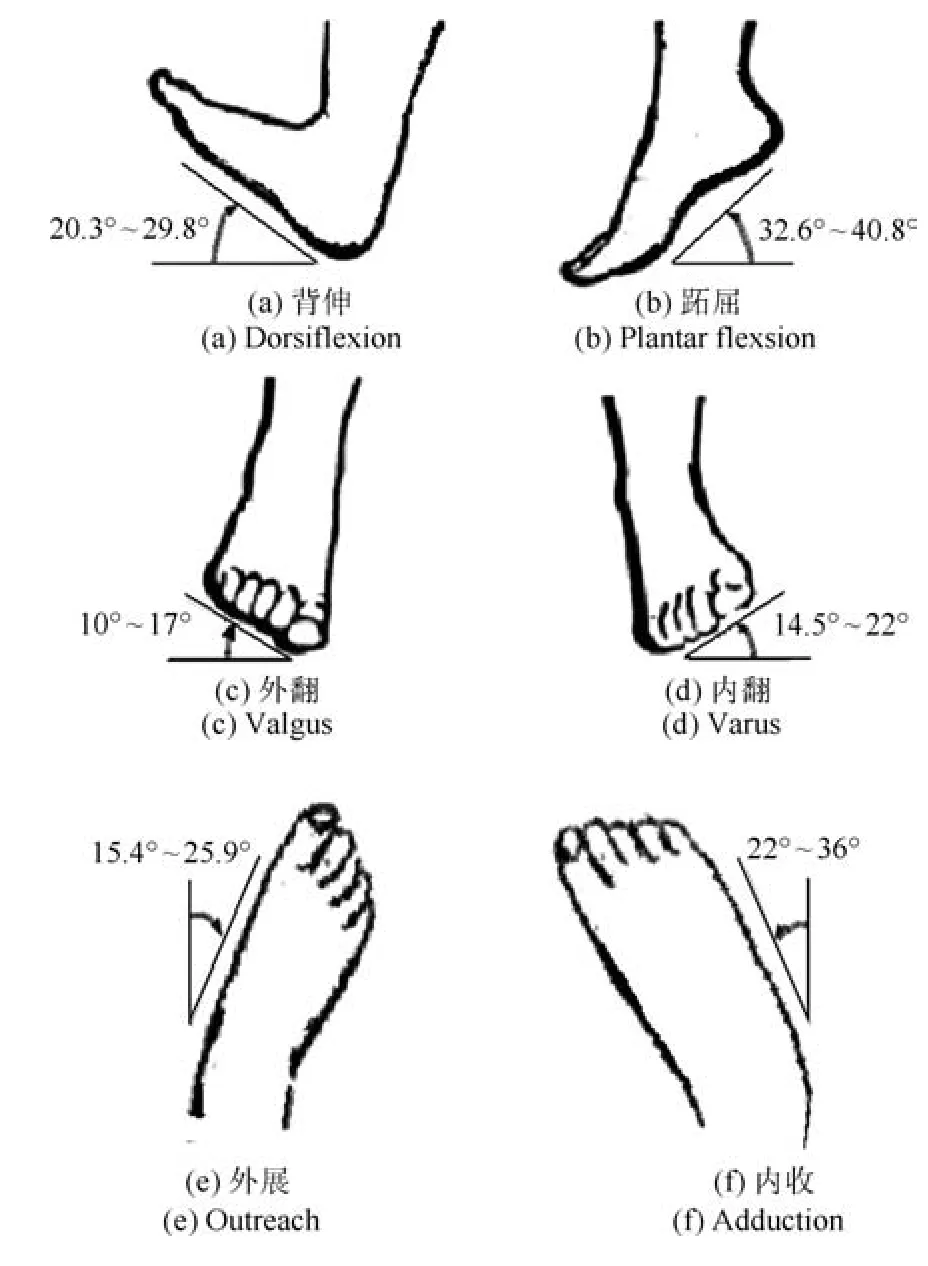
圖1 踝關節運動模式及其運動范圍Fig.1 Ankle movement patterns and their ranges of movement

根據上述踝關節運動形式及特點可知,可將踝關節的運動簡化為繞三個垂直軸X、Y、Z的旋轉運動[13],如圖2所示.

由以上分析,所設計的踝關節康復機構在三個正交方向的最大轉動角度須滿足圖1的要求,這是踝關節康復機構設計的基礎.

1.2 機構簡介

與串聯機構相比,并聯機構具有剛度大、運動精度高、慣性小、載荷分布均勻、結構對稱且具有各向同性等特點,而且設計制造和控制成本相對較低.結合踝關節康復運動的特點及要求,將機構設計成并聯形式要優于串聯形式.如圖3所示,一種基于3-UPS/RRR的并聯踝關節康復機構由底座、動平臺、三個并聯支鏈和一個約束支鏈構成,約束支鏈由三個轉動軸線相互正交的轉動副R1R2R3(等效為球副)組成,軸線相交于一點,即為機構轉動中心和踝關節轉動中心重合的點.三個并聯支鏈均是由一個虎克副、一個移動副和一個球副組成.

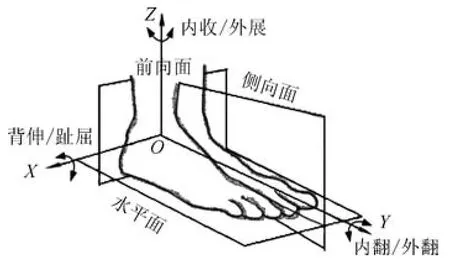
圖2 腳踝運動Fig.2 Ankle joint movement

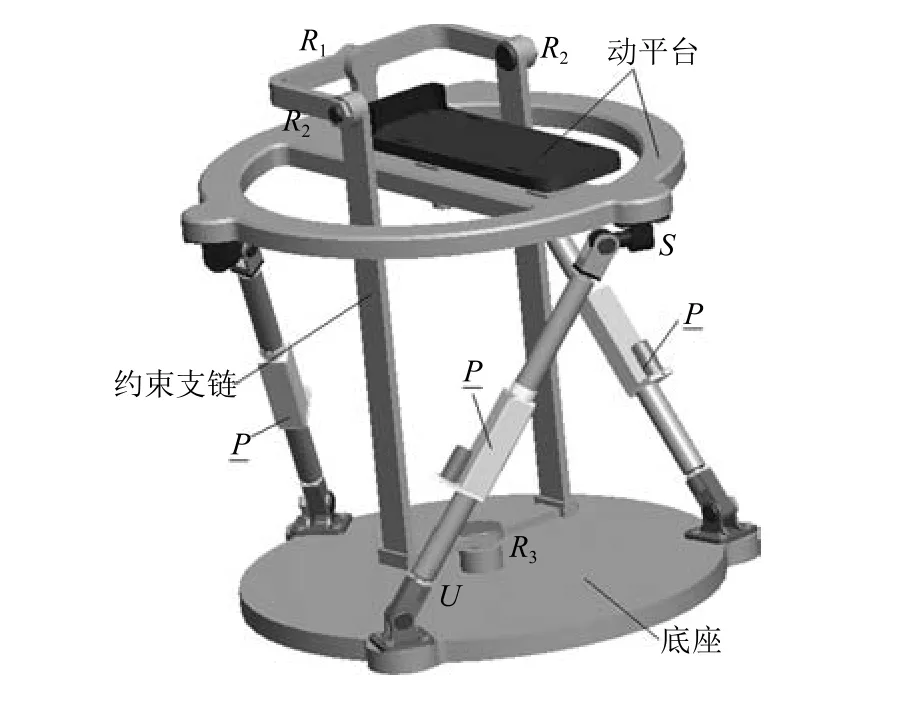
圖3 并聯踝關節康復機構模型Fig.3 The model of parallel mechanism for ankle rehabilitation

對于3-UPS/RRR三自由度并聯機構,動平臺運動過程中,當出現兩個或三個主動支鏈相互平行時,不難發現此時機構處于奇異位形,表現為機構失去穩定,運動學、動力學性能瞬時發生突變,不能正常地傳遞運動和力.對于該奇異性問題,文獻[14]提出通過約束或冗余驅動來消除奇異,文獻[15?16]提出規劃路徑的方法來規避奇異位形.由于踝關節康復運動所需工作空間有限,故采取三個主動支鏈以相同傾斜角布置于動平臺和底座之間來避開奇異位形.根據人腳的尺寸范圍初步確定動平臺和定平臺底座圓盤的半徑,同時考慮結構的緊湊性,設定兩平臺間的高度;通過改變動平臺上均分點Ai的位置,定平臺上均分點Bi位置不變,也即改變如圖4中α的角度值,初選出工作空間大于圖1中踝關節運動范圍的α角度值;以可操作度小于5為目標函數,從初選的角度值中選取符合條件的位置,從而確定一個滿足條件的較小的α角度范圍,最后從該角度范圍內選取較優的位置,即為最終Ai點的位置,文中選取的α角度值為72°.Ai點的位置確定后,支鏈的傾斜角也就確定了.工作過程中使用電機驅動這三條主動支鏈來實現機構的三個轉動運動,機構沒有冗余支鏈,結構相對簡單且在一定的工作空間內減少了干涉的可能.

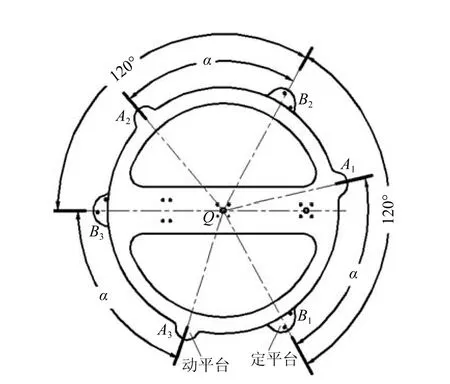
圖4 動平臺在定平臺上投影圖Fig.4 The projection of moving platform on the fxed platform

如圖5所示,動平臺由兩部分組成:上平臺和下平臺.實際操作過程中,患者將腳置于上平臺上進行康復訓練,通過調節螺釘改變上下平臺間的相對位置,通過連接螺栓調節擋板在上平臺上的位置,這樣就能保證患者踝關節的轉動中心與機構的轉動中心重合,同時可通過擋板與彈性綁帶將腳綁縛在上平臺上,避免在康復運動中,人腳與上平臺出現較大的相對位移,造成不必要的損傷.此種設計不僅能改善人(踝關節)機(康復機構)之間的相容性,而且能使康復訓練更加安全有效.

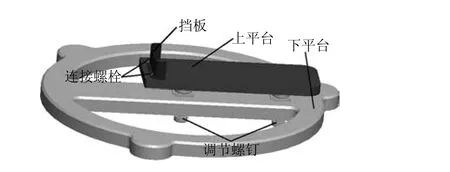
圖5 動平臺機構模型Fig.5 The moving platform mechanism mode

2 機構運動學分析

3-UPS/RRR并聯踝關節康復機構的機構簡圖如圖6所示.符號定義如下:定坐標系O-XbYbZb原點位于點O,動坐標系T-xtytzt原點位于旋轉中心點T,定坐標系方向如圖6中所示沿三個轉動副軸線方向,初始位置時兩坐標系方向一致,O與T重合.O′為軸Zb與底座的交點,Q為軸Zb與動平臺的交點,QAi=O′Bi=d,OO′=L3,其中Ai、Bi、Si(i=1,2,3)分別為球副中心、虎克副中心和移動副的運動位移.初始狀態下,虎克副的第一根軸線與Xb平行,第二根軸線與Yb平行.圖中轉動副R2、R1、R3的軸線正交于一點,可等效為一個連接動平臺與定平臺的球關節,轉過的角度依次記為α、β、γ.

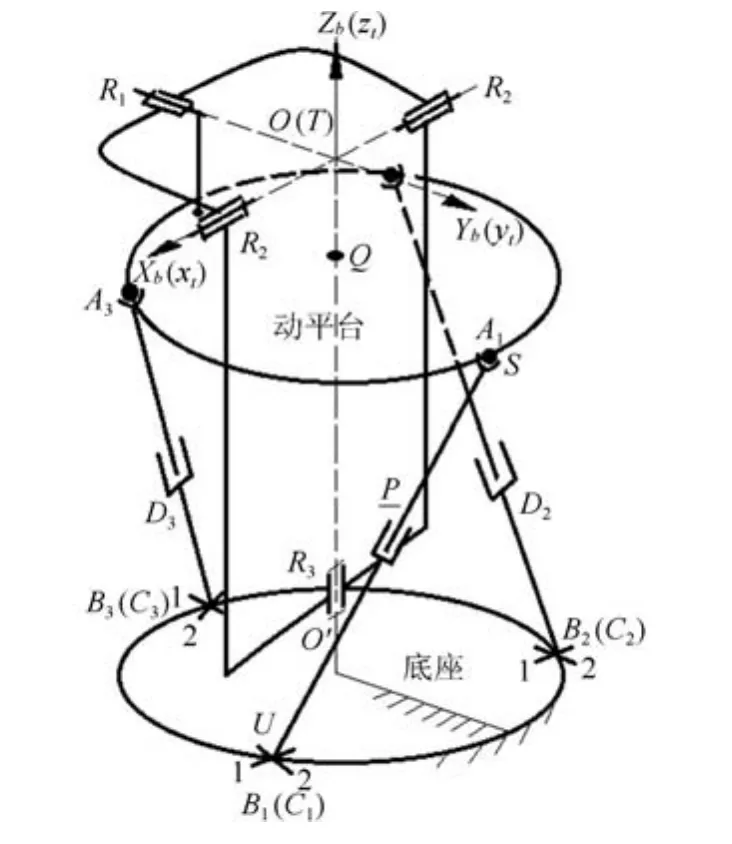
圖6 3-UPS/RRR并聯機構簡圖Fig.6 The sketch of 3-UPS/RRR parallel mechanism

支鏈坐標系如圖7所示,原點在虎克副幾何中心點Bi的坐標系Bi-XBiYBiZBi,軸XBi與虎克副的第一根軸線重合,軸YBi與機構處于初始位形時虎克副的第二根軸線重合,軸

Ci-XCiYCiZCi是建立在桿CiDi上的坐標系,原點為虎克副的幾何中心點Ci,軸YCi與虎克副的第二根軸線重合,軸ZCi與桿CiDi重合,軸為原點在球副幾何中心點Ai的坐標系,并與Ci-XCiYCiZCi坐標系平行.其中第i支鏈上繞虎克副第一根軸線的旋轉角表示為qi1,繞虎克副第二根軸線的旋轉角表示為qi2,繞Z軸旋轉的角度表示為q3.

動平臺姿態的表達有多種方法,由于此處等效球關節的特征,選用Z-X-Y歐拉角描述.α表示繞X軸的旋轉角度(X歐拉角表示背伸/跖屈),β為繞Y軸的旋轉角度(Y歐拉角表示內翻/外翻),γ是繞Z軸的旋轉角度(Z歐拉角表示內收/外展).一旦角度給定,動平臺相對于固定底座的旋轉矩陣ROT可以表示如下:

其中,c,s分別為cos、sin的簡稱.

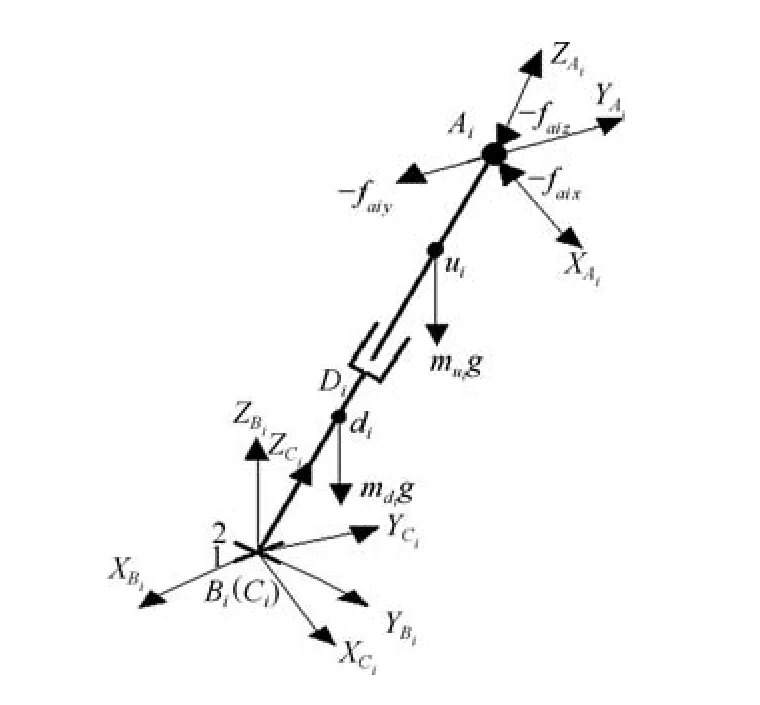
圖7 支鏈坐標簡圖Fig.7 Diagram of the branched coordinate

2.1 自由度計算

由踝關節康復機構簡圖(圖6)可知,該機構由底座、動平臺、主動支鏈AiBi(i=1,2,3)以及約束支鏈R1R2R3組成,約束支鏈R1R2R3可等效為一個球關節,即底座與動平臺由三個UPS支鏈和一個等效球關節連接.根據Kutzbach-Grbler自由度計算公式,機構的自由度可表示為如下形式:

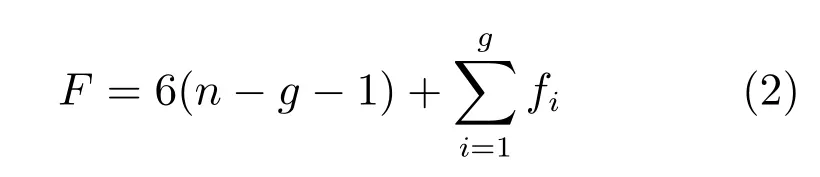
機構由3個UPS支鏈與1個RRR支鏈組成,桿件數n=8,鉸鏈數g=10,分別是4個球副、3個虎克副、3個移動副,則機構自由度F可由式(2)計算得到:

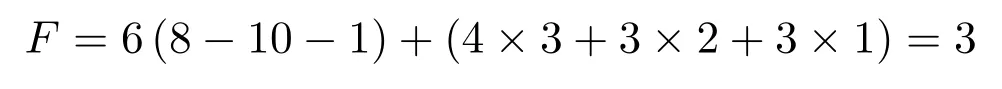
3-UPS/RRR機構具有3個自由度,而約束支鏈只能在三個正交方向轉動,故整個機構的運動為繞X、Y和Z軸的轉動,能夠提供踝關節康復所需運動.

2.2 位置逆解

已知動平臺繞固定坐標系的輸出轉角α、β、γ,求出3個主動支鏈的驅動器輸入位移S1、S2、S3,就是該機構的運動學位置逆解.球鉸中心點Ai的位置矢量可分別寫為:

2.3 速度與加速度分析

球鉸中心點Ai的速度可表示為:

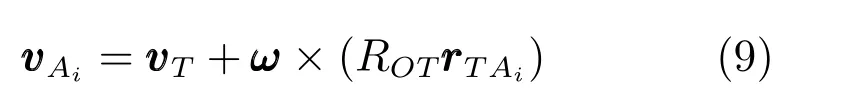
球鉸中心點Ai的加速度可表示為:

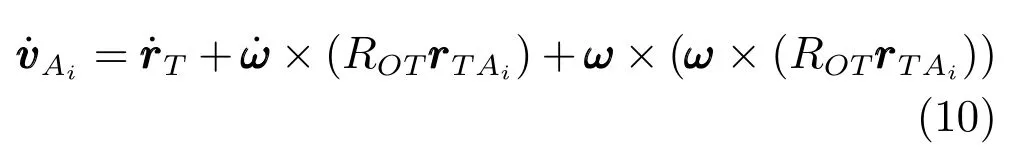
點Ai的速度分別向Ai-XAiYAiZAi坐標系的各坐標軸分解有:

2.4 速度雅可比矩陣

速度雅可比矩陣又稱作機構的一階影響系數,是機構輸入輸出構件間的速度比例矩陣.對于3-UPS/RRR并聯踝關節康復機構,雅可比矩陣是對機構進行運動性能分析和靜力學分析的關鍵.由式(12)可以得到,驅動三個移動副時,機構的雅可比矩陣[17]滿足:

3 運動性能分析

3.1 工作空間分析

工作空間是并聯機構動平臺參考點可達范圍的集合,其大小直接影響著并聯機構的實際應用價值,而且是衡量機構工作能力的一個重要指標.本文研究的踝關節康復機構的工作空間定義為:滿足驅動與結構參數的條件下,動平臺所有位姿的集合,機構的結構參數列于表1中.

表1 機構的結構參數Table 1 The architectural parameters of the mechanism

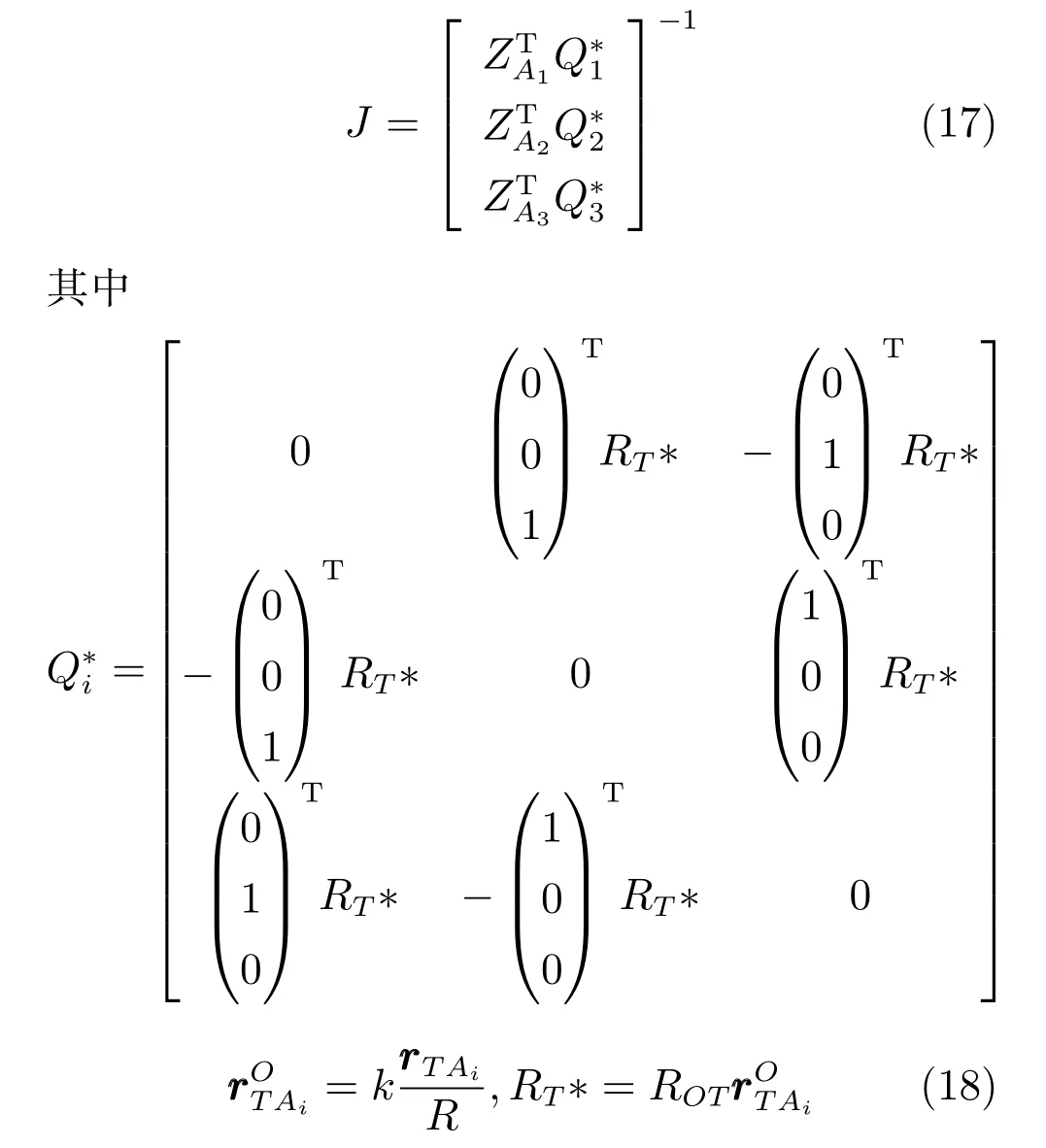
在限定移動副的移動距離為±0.55m,虎克副的轉動角度為±35°的條件下,借助Matlab軟件利用搜索法對機構的工作空間進行仿真分析,結果如圖8所示,通過對工作空間圖投影可得機構動平臺的運動范圍如表2所示.將表2中的數據與圖1中的統計數據進行比較發現,機構可達的工作空間范圍大于踝關節的運動范圍,故本文提出的3-UPS/RRR并聯機構符合踝關節康復機構設計的基本要求.

圖8 并聯機構工作空間Fig.8 The working space of parallel mechanism

表2 康復機構的運動范圍Table 2 The movement range of rehabilitation mechanism

3.2 可操作度分析

可操作度是反映機構動平臺在位移和姿態方面可操作能力的一個度量,也是評價機構在某位姿下靈活性的一個指標[20].當機構處于奇異位形時,可操作度w=0,此時機構將失去沿某一方向的活動能力,靈活性也最小,因此,應當盡量避免機構接近奇異位形.當機構處于非奇異位形時,定義雅可比矩陣與其轉置矩陣乘積的行列式值的開方為機構的可操作度[21].即:

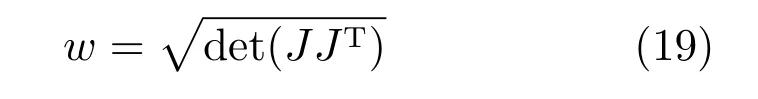
在規定工作空間內對機構的可操作度進行仿真分析,以α、β為連續變量,γ取不同的角度值,可得到不同姿態下,機構可操作度的分布情況,通過γ取三個不同角度值(一個中間點和兩個邊界位置點(γ=?20°,0°,20°))時,機構可操作度的變化圖像,即可反映機構在整個康復運動范圍內可操作度的分布情況,如圖9～11所示.

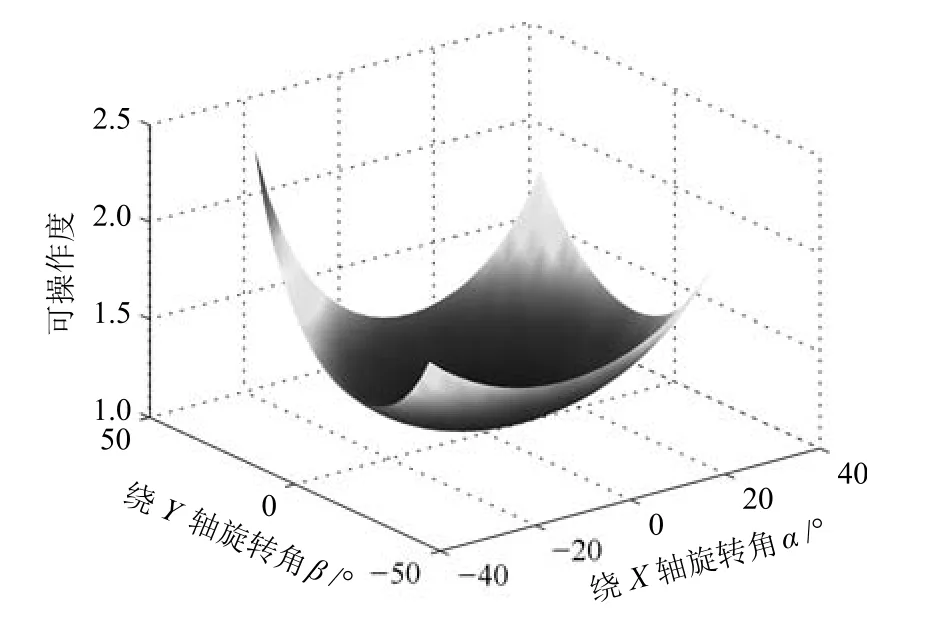
圖9 γ=?20°時機構的可操作度Fig.9 The mechanism's operation atγ=?20°

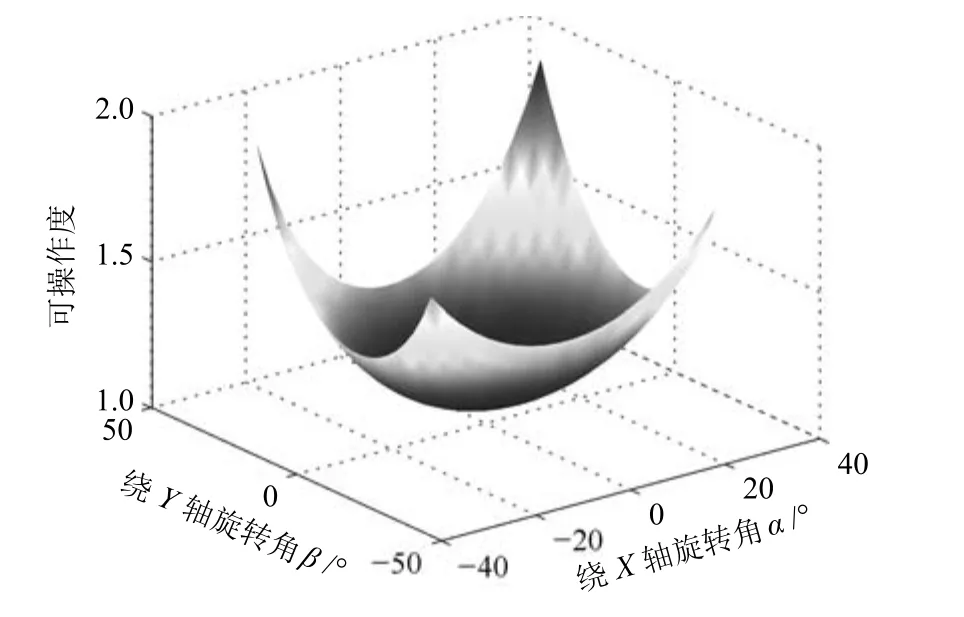
圖10 γ=0°時機構的可操作度Fig.10 The mechanism's operation atγ=0°

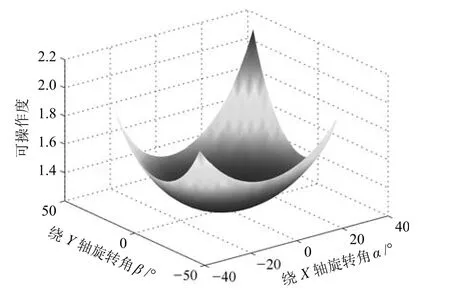
圖11 γ=20°時機構的可操作度Fig.11 The mechanism's operation atγ=20°

由仿真圖可知,該機構的可操作度值在1到3之間變化,沒有零值,且變化連續平穩,說明在該結構參數下,工作空間內機構沒有奇異位形,可操作性良好.但在實際應用中,可操作度只能表示機構在某一時刻的操作性能,對于靈巧性的評價也具有局限性,并不能描述當機構存在輸入偏差時對輸出偏差的影響.因此,還需對3-UPS/RRR并聯踝關節康復機構的靈巧性作進一步的分析.

3.3 靈巧性分析

靈巧性分析反映的是機構的綜合運動性能,Salisbury等提出采用雅可比矩陣的條件數作為機構的靈巧性指標[22].設機構動平臺的輸出角速度矢量為ω,輸入速度為,則該機構的運動方程為J是機構的無量綱速度雅可比矩陣.當輸入速度的偏差為輸出角速度偏差為? ω時,運動方程可寫為:

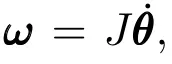
根據矩陣論的范數理論有:

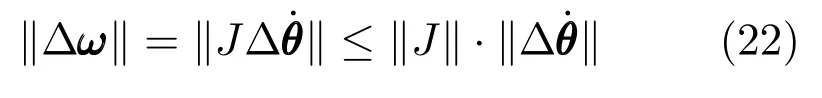
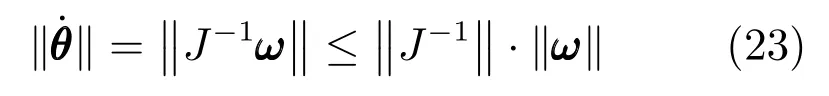
由式(22)和(23)可得:

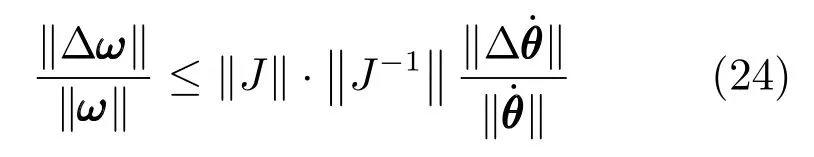
令K=‖J‖·‖J?1‖,則K即為雅可比矩陣J的條件數.它是衡量雅可比矩陣的逆矩陣精確度的一個度量,取值范圍是:1≤K＜∞.若K值較大,則該矩陣的逆矩陣精度較低,此時輸入速度較小的偏差將導致操作器較大的偏差.所以在機構設計時,應使雅可比矩陣條件數在其操作范圍內盡量為較小的值.當K等于1時,機構處于最佳的傳遞性能,此時機構處于運動學各向同性[23].從條件數的取值范圍可知,其變化范圍很大,所以為分析方便起見,定義雅可比矩陣條件數的倒數1/K為靈巧性評價指標.在規定的工作空間內對機構的條件數倒數進行計算分析.同可操作度分析,分別繪制了γ=?20°,0°,20°時機構的條件數倒數分布,如圖12～14所示.

觀察圖12～14可知,機構條件數倒數的最大值為0.71,出現在中間位置,隨著機構轉動到工作空間的邊界位置,條件數倒數逐漸減小至最小值0.25,變化趨勢平緩,沒有突變.對比文獻[13,17]中靈巧性分析結果可知,3-UPS/RRR踝關節康復機構在中間工作空間及整個工作空間內同樣具有較好的靈巧性能.

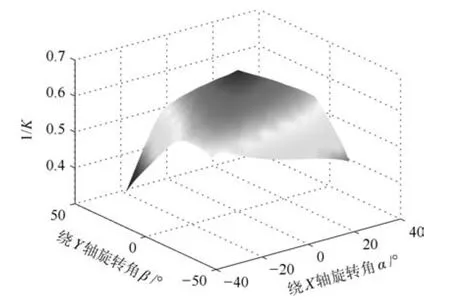
圖12 γ=?20°時機構的條件數倒數Fig.12 The mechanism's condition number reciprocal atγ=?20°

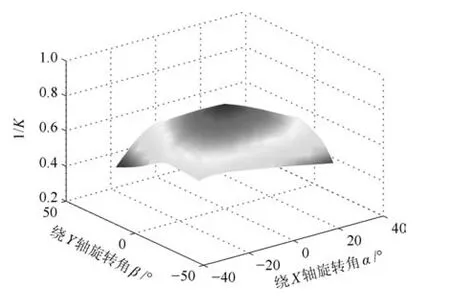
圖13 γ=0°時機構的條件數倒數Fig.13 The mechanism's condition number reciprocal atγ=0°

圖14 γ=20°時機構的條件數倒數Fig.14 The mechanism's condition number reciprocal atγ=20°

3.4 剛度分析

并聯機構剛度是指末端動平臺在外力作用下,由于彈性元件的變形引起位移大小的度量,產生變形的有連桿本身、連接鉸鏈及關節驅動裝置.對于多數機構而言,在假定連桿和鉸鏈是剛性的前提下,變形的主要來源是傳動、減速裝置和伺服驅動系統[24].為了簡便起見,通常將驅動關節的剛度(包括傳動減速裝置)用一彈簧常數ki來表示,即:

式中,fi為驅動力,?qi為fi作用產生的附加變形量.

忽略重力和關節摩擦力的影響,根據雅可比矩陣可得,作用在動平臺上的力矢量與驅動力矢量滿足:

其中,J為機構速度雅可比矩陣.

機構有三個相同的驅動支鏈,由結構的對稱性,可認為每個驅動支鏈的剛度相等,則驅動系統剛度為k=diag{k1,k2,k3},其中k1=k2=k3=1[25].將式(25)寫成矢量形式:

綜合式(26)～(28)可得:

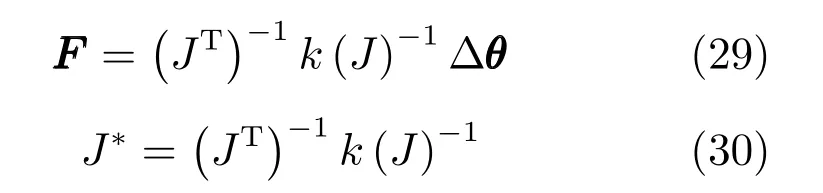
式(30)中,J?即為機構的剛度雅可比矩陣.現假設作用在動平臺的力矢量的模為單位1,即則可求得末端動平臺位移量的極值.方法如下:

首先,建立拉格朗日方程:

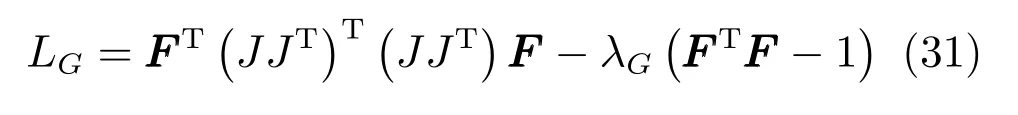
式中,λG為拉格朗日乘子.

然后,由條件極值求解需滿足的條件得:

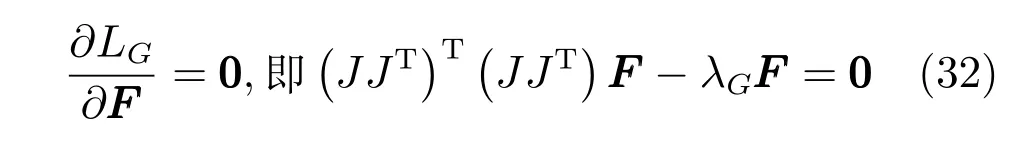
其中,λG也是(JJT)T(JJT)的特征值.

最后,由特征值求解可得到,末端動平臺位移量‖?θ‖的極大值和極小值:

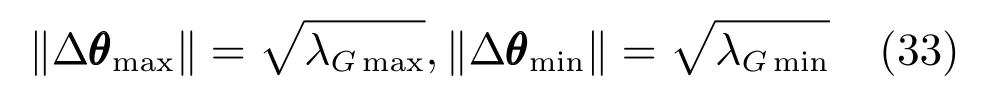
機構沿位移極大值的方向,其剛度最差,沿極小值的方向,其剛度最好.但在實際應用中很難出現最小位移的情況,因而最小位移量(特征值極小值)并不能代表機構的剛度性能,故取位移極大值來衡量機構的剛度性能[24?25],表達式如下:

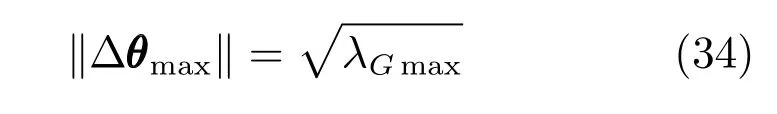
‖?θmax‖表示機構動平臺在受到單位力的作用時最大的位移量.因此,機構在任意位形下,‖?θmax‖越小,機構的剛度性能越好.同可操作度分析,在工作空間內,分別繪制了γ=?20°,0°,20°時機構剛度性能的分布圖,如圖15～17所示.

由圖15～17分析可知,機構在工作空間內,‖?θmax‖值越接近中間區域越小,也即剛度性能越好,由圖1中踝關節運動范圍可以發現,踝關節康復運動也主要集中在中間區域,也即剛度性能較好的區域,故機構適合用于踝關節康復訓練.

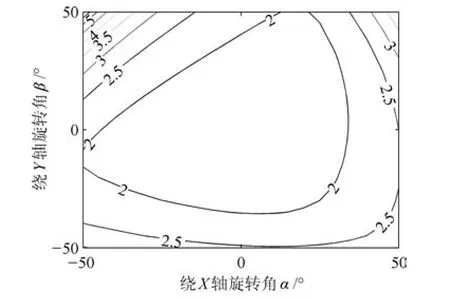
圖15 γ=?20°時機構的剛度性能Fig.15 The mechanism's stifness performance atγ=?20°

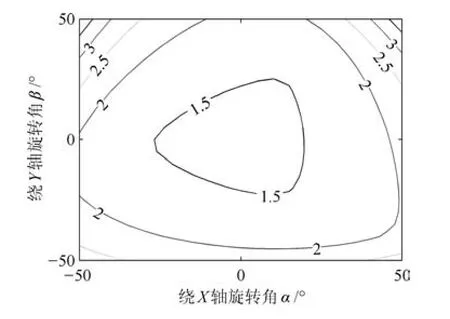
圖16 γ=0°時機構的剛度性能Fig.16 The mechanism's stifness performance atγ=0°

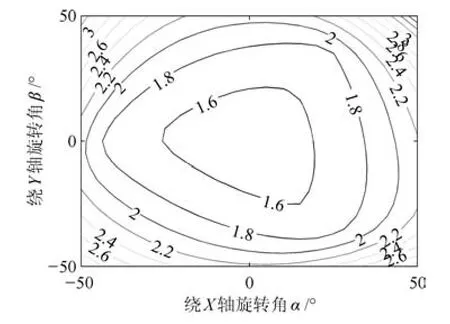
圖17 γ=20°時機構的剛度性能Fig.17 The mechanism's stifness performance atγ=20°

4 靜力學性能分析

4.1 靜力雅可比矩陣

靜力雅可比矩陣表征了機構驅動器輸入力或力矩與動平臺靜態操作力或力矩之間的映射關系[24],是對機構進行靜力學性能分析的重要依據,可利用速度雅可比矩陣通過虛功原理求得.根據動平臺的運動特點,假設動平臺在外力矩M的作用下,動平臺的虛轉角為??,相應地輸入端驅動關節在驅動力矩τ作用下虛轉角為則驅動力矩τ及外力矩M所作虛功為:

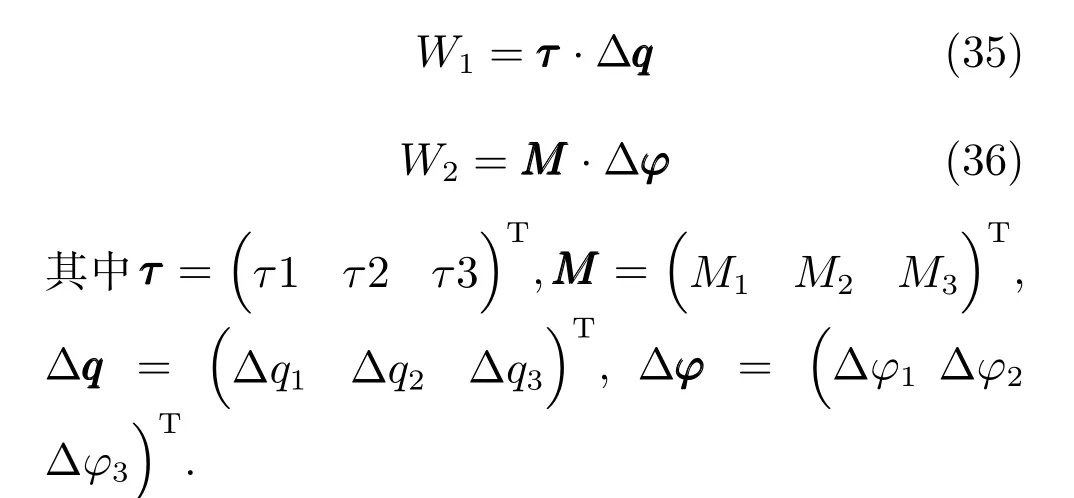
由虛功原理知:

代入式(35)及(36)整理得:

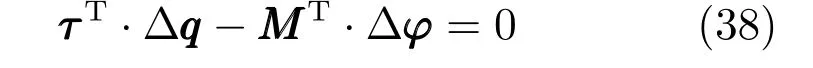
代入式(38)得:

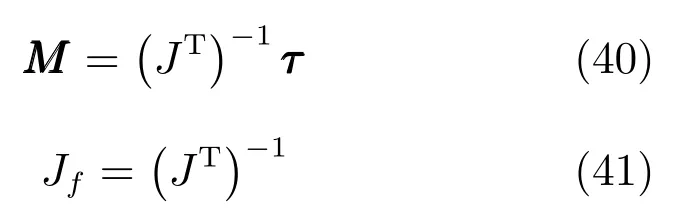
所得Jf即為機構靜力雅可比矩陣.

4.2 力矩傳遞性能分析

3-UPS/RRR并聯機構只有三個轉動方向的自由度,運動過程中主要傳遞力矩.故對靜力雅可比矩陣的關系式(40)取2范數,代入式(41)得:

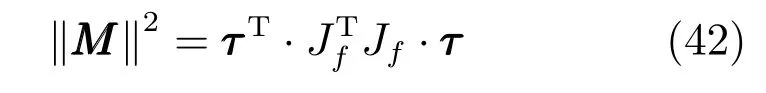
設輸入量為單位力矩矢量,即:

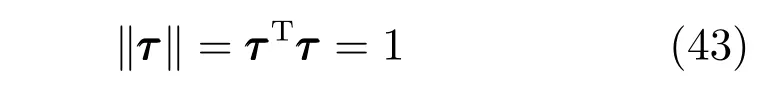
構造如下拉格朗日方程:

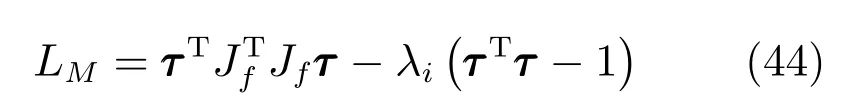
式中λi為拉格朗日乘子,則輸出力矩取極值的條件為:

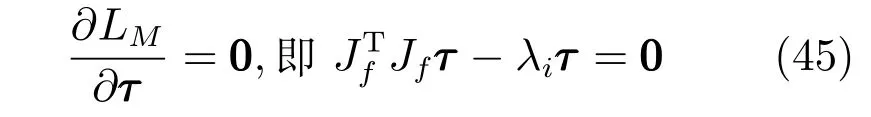
其中,λi也為矩陣的特征值,由此得輸出力矩M的極值為:

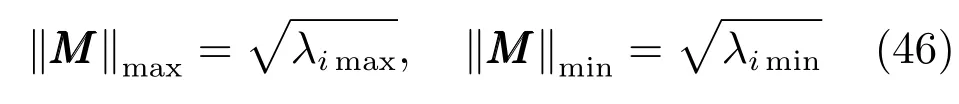
機構在運動過程中只能在一個方向出現最大輸出力矩,但在實際應用中很難出現最大輸出力矩的情況,因此,最大輸出力矩并不能表征機構的力矩傳遞性能.故將驅動力矩為單位向量時,輸出力矩極小值作為評價機構力矩傳遞性能T(M)的指標[25?26],且極小值越大,機構的力矩傳遞性能越好,表達式如下:

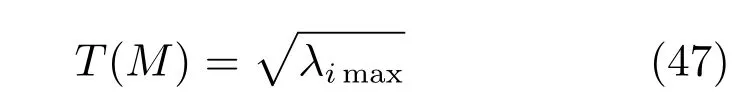
根據式(47)分別繪制當γ=?20°,0°,20°時機構力矩傳遞性能指標,如圖18～20所示.

由圖18～20分析可知,在工作空間內,T(M)值主要集中在0.6到0.8之間,且隨著轉動角度的增大,力矩傳遞性能逐漸減小且變化趨勢比較平緩均勻.但是不難看出,在中間區域力矩傳遞性能要優于邊緣部分,而踝關節康復運動也主要集中在中間區域,因此滿足踝關節康復訓練要求.

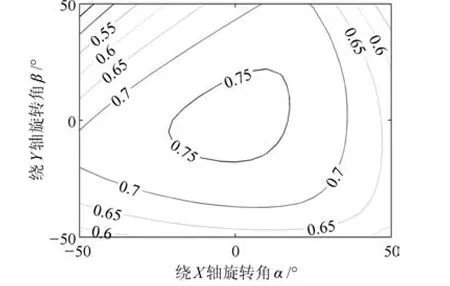
圖18 γ=?20°時機構的力矩傳遞性能Fig.18 The mechanism's torque transmission performance atγ=?20°

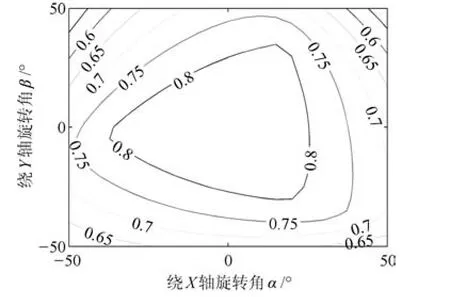
圖19 γ=0°時機構的力矩傳遞性能Fig.19 The mechanism's torque transmission performance atγ=0°

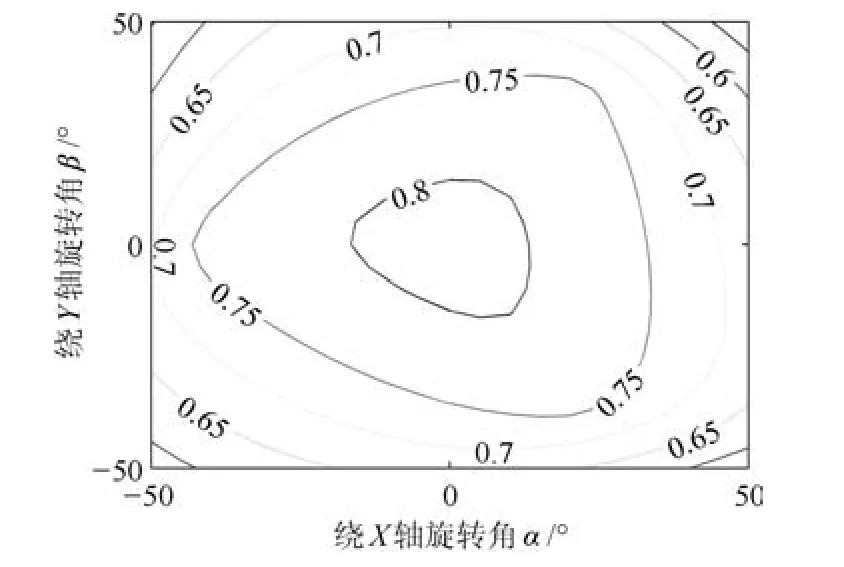
圖20 γ=20°時機構的力矩傳遞性能Fig.20 The mechanism's torque transmission performance atγ=20°

5 動力學分析

機構動力學分析的主要目的是研究機構運動參數與驅動力之間的映射關系,它是機構優化設計、動態性能評價及運動控制的基礎.文獻[27]運用牛頓-歐拉法建立了Tricept并聯機構的逆動力學方程,并對驅動優化問題進行了研究.文獻[28]運用牛頓-歐拉法分析2UPS-2RPS機構的逆動力學問題,在給定動平臺的運動規律和外力后求解出所需驅動力和約束力矩.基于3-UPS/RRR并聯踝關節康復機構,運用牛頓-歐拉法,對機構的逆動力學問題進行分析.

5.1 主動支鏈動力學

如圖7所示,設在支鏈坐標系下第i支鏈作用于動平臺的三維力向量在定坐標系下重力加速度向量則相對坐標原點Ci,運動支鏈合外力矩向量可表示為:

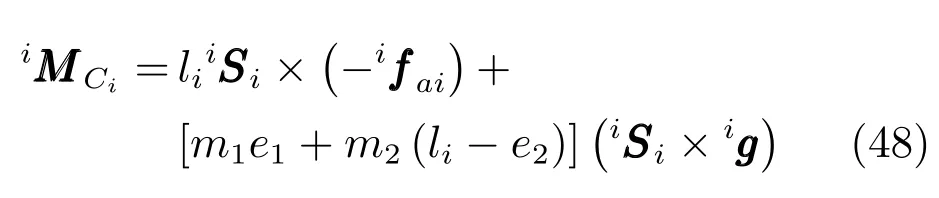
合慣性力矩向量為:

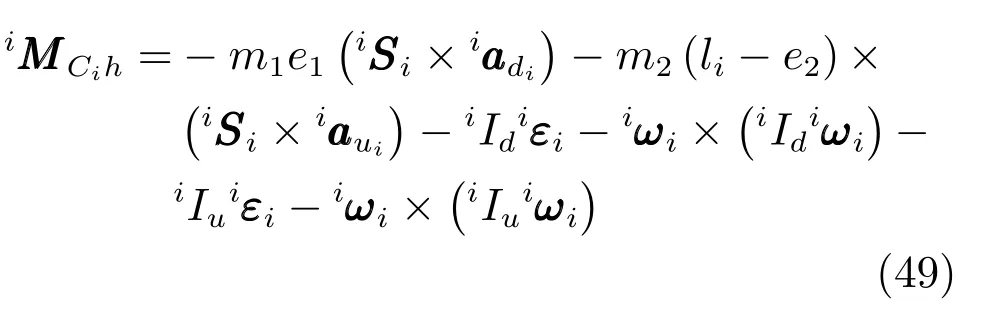
根據歐拉方程,得到力矩平衡方程:

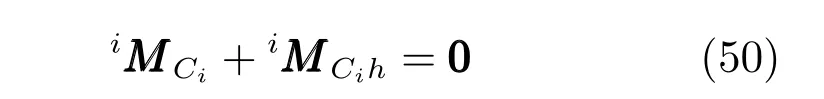
式中,li為支鏈i的長度,為支鏈坐標系下軸ZCi所在方向的單位向量;m1、m2分別為下缸體和活塞的質量;e1、e2分別為下缸體質心di到Bi的距離和活塞的質心ui到Ai的距離;iId、iIu分別為下缸體和活塞在第i支鏈坐標系下關于質心的慣性矩陣;iωi、iεi分別為支鏈坐標系下i支鏈的角速度和角加速度,且

5.2 動平臺動力學

對動平臺進行分析,由牛頓定理得:

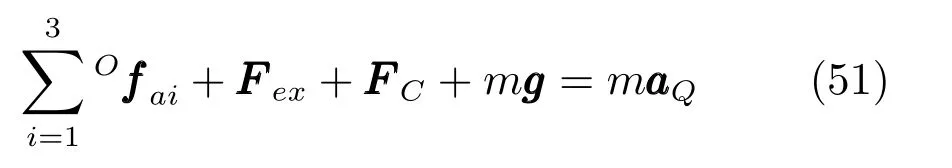
式中,Q為動平臺的質心;m為動平臺的質量;為定坐標系下支鏈i作用于動平臺的力;為作用于動平臺的外力,為約束支鏈對動平臺的約束力,由動平臺只有轉動自由度知

由歐拉方程得到,動平臺在動坐標系下關于質心的力矩平衡方程為:

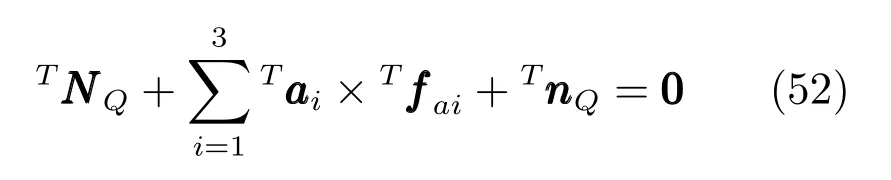
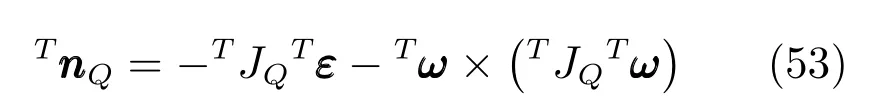
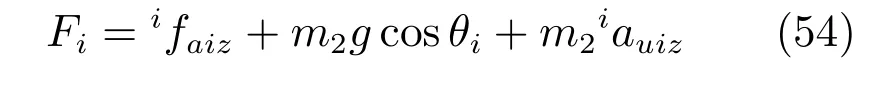
式中,θi為支鏈i與定平臺的夾角.

5.3 算例仿真給定3-UPS/RRR并聯機構的幾何和物理參數如下:機構所受外載荷動坐標系下動平臺所受載荷力矩矢量N·m,重力加速度cosθi=0.589.

考慮踝關節康復運動需要且不失一般性,設動平臺初始姿態:(α0β0γ0)=(0?π/9?π/18);初始角速度:Tω0=(0.1 0.1 0.1)Trad/s;角加速度:Tε=(0.02 0.02 0.02)Trad/s2.

令時間t=5s,經Matlab編程計算,可得三個UPS支鏈驅動力和約束支鏈的約束力,分別如圖21和圖22所示.

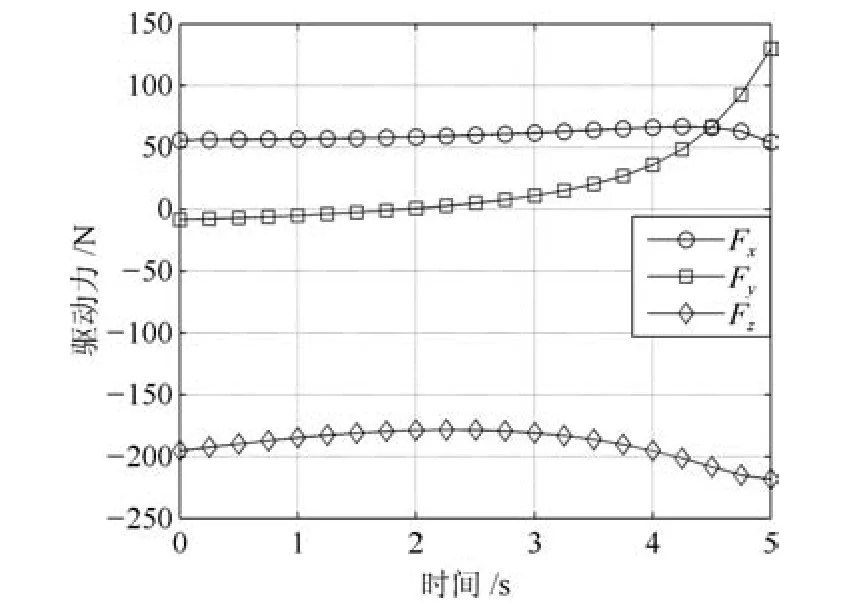
圖22 約束支鏈的約束力Fig.22 The constraint force of constraint branches

由圖21可知,驅動力在-100～100N之間,主要用于實現動平臺三個方向的轉動,由于給出的運動軌跡是一條不規則的曲線,三個驅動力的變化沒有規律性,更具有一般性.圖22中,約束力Fx與Fy在0～200N之間,主要用來平衡支鏈驅動力在x、y方向的分量和動平臺的慣性力,Fz比Fx和Fy大,是因為Fz需要平衡動平臺的重力、施加的外力、驅動力在z方向的分量和動平臺的慣性力.

6 結論

本文結合踝關節的解剖結構及其運動特性,在分析現有踝關節康復機構的基礎上,提出一種3-UPS/RRR并聯踝關節康復機構.該機構不僅能滿足踝關節康復所需的背伸/跖屈、內翻/外翻、內收/外展三個方向的運動,還能保證機構的轉動中心與踝關節的運動中心重合.機構采用三個伸縮支鏈驅動,結構簡單,沒有冗余支鏈,且采用主動支鏈傾斜布置避開機構的奇異位形,通過搜索算法找到了合適的傾斜角以滿足踝關節康復運動需要.機構位置反解及工作空間的求解分析表明機構能很好地完成踝關節康復訓練.基于速度雅可比矩陣的仿真分析結果表明,機構具有良好的運動學性能與靜力學性能,適合用于踝關節康復訓練.利用牛頓-歐拉法建立機構的逆動力學方程,求解出支鏈驅動力、約束支鏈約束力與運動參數間的映射關系,并通過實例仿真為3-UPS/RRR機構的康復運動控制和驅動系統的選取提供參考.

1 Yao Tai-Shun,Meng Xian-Jie.Ankle Surgery.Beijing:Traditional Chinese Medicine Press,1998.21?36 (姚太順,孟憲杰.踝關節外科.北京:中國中醫藥出版社,1998. 21?36)

2 Li D,Zhao T S,Bian H.Bio-syncretic mechanism system and its application in the rehabilitation engineering.In:Proceedings of the 2008 International Mechanisms and Machine Science Conference.Dalian,China,2008.28?31

3 Jiao Shuang,Yan Ru-Yun.The research progress on prevention sports injury of ankle proprioception training.Chinese Journal of Sports Medicine,2009,28(6):713?716 (焦爽,閆汝蘊.本體感覺訓練預防踝關節運動損傷研究進展.中國運動醫學雜志,2009,28(6):713?716)

4 Girone M J,Burdea G C,Bouzit M.The“Rutgers Ankle”orthopedic rehabilitation interface.Proceedings of the ASME Haptics Symposium,1999,67:305?312

5 Girone M,Burdea G,Bouzit M,Popescu V,Deutsch J E.A Stewart platform-based system for ankle telerehabilitation.Autonomous Robots,2001,10(2):203?212

6 Saglia J A,Tsagarakis N G,Dai J S,Caldwell D G.A high performance 2-Dof over-actuated parallel mechanismfor ankle rehabilitation.In:Proceedings of the 2009 International Conference on Robotics and Automation.Kobe, Japan:IEEE,2009.2180?2186

7 Yu Hai-Bo.Design of System of Parallel Ankle Rehabilitation Device[Master dissertation],Yanshan University, China,2006. (于海波.并聯式踝關節康復機器人系統設計[碩士學位論文],燕山大學,中國,2006.)

8 Liu G Q,Gao J L,Yue H,Zhang X J,Lu G D.Design and kinematics analysis of parallel robots for ankle rehabilitation.In:Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems.Beijing,China:IEEE,2006.253?258

9 Wang C Z,Fang Y F,Guo S,Chen Y Q.Design and kinematical performance analysis of a 3-RUS/RRR redundantly actuated parallel mechanism for ankle rehabilitation.Journal of Mechanisms and Robotics,2013,5(3):041003-1?041003-11

10 Bian Hui,Zhao Tie-Shi,Tian Xing-Bin,Li Dan,Pan Wang. Bio-syncretic rehabilitation mechanism and its application.Robot,2010.32(4):470?477 (邊輝,趙鐵石,田行斌,李丹,潘旺.生物融合式康復機構及其應用.機器人,2010,32(4):470?477)

11 Leardini A,O'Connor J J,Catani F,Giannini S.Kinematics of the human ankle complex in passive fexion;a single degree of freedom system.Journal of Biomechanics,1999,32(2):111?118

12 Tsoi Y H,Xie S Q.Design and control of a parallel robot for ankle rehabilitation.International Journal of Intelligent Systems Technologies and Applications,2010,8(1?4): 100?113

13 Yu Run-Tian,Fang Yue-Fa,Guo Sheng.Design and kinematic performance analysis of a cable-driven parallel mechanism for ankle rehabilitation.Robot,2015,37(1):53?62, 73 (禹潤田,方躍法,郭盛.繩驅動并聯踝關節康復機構設計及運動性能分析.機器人,2015,37(1):53?62,73)

14 Yiu Y K,Cheng H,Xiong Z H,Liu G F,Li Z X.On the dynamics of parallel manipulators.In:Proceedings of the 2001 IEEE International Conference on Robotics and Automation.Seoul,South Korea:IEEE,2001.146?154

15 Sen S,Dasgupta B,Mallik A K.Variational approach for singularity-free path-planning of parallel manipulators.Mechanism and Machine Theory,2003,38(11):1165?1183

16 Bandyopadhyay S,Ghosal A.Analysis of confguration space singularities of closed-loop mechanisms and parallel manipulators.Mechanism and Machine Theory,2004,39(5):519?544

17 Li Jian-Feng,Li Shi-Cai,Tao Chun-Jing,Ji Run,Xu Cheng-Hui,Zhang Zhao-Jing.Parallel 2-UPˉS/RˉRR ankle rehabilitation mechanism and kinematic performance analysis.Robot,2016,38(2):144?153 (李劍鋒,李世才,陶春靜,季潤,徐成輝,張兆晶.并聯 2-UPˉS/RˉRR 踝關節康復機構及運動性能分析.機器人,2016,38(2):144?153)

18 Wang Man-Xin,Huang Tian.Kinematics analysis and dimensional synthesis of a plane symmetric 3-SPˉR parallel manipulator.Journal of Mechanical Engineering,2013,49(15): 22?27 (汪滿新,黃田.面對稱3-SPˉR并聯機構的運動學分析與尺度綜合.機械工程學報,2013,49(15):22?27)

19 Chen Xiu-Long,Gao Qing,Zhao Yong-Sheng.Dexterity measures of 4-UPS-UPU parallel coordinate measuring machine.Computer Integrated Manufacturing Systems,2012,18(6):1200?1208 (陳修龍,高慶,趙永生.4-UPS-UPU并聯坐標測量機的靈巧度研究.計算機集成制造系統,2012,18(6):1200?1208)

20 Rao Qing,Bai Shi-Xian.Manipulability analysis and deeinition of 6-SPS stewart robot.Robot,1994,16(6):345?349 (饒青,白師賢.6-6型Stewart機器人的可操作性分析及其定義.機器人,1994,16(6):345?349)

21 Yoshikawa T.Manipulability of robotic mechanisms.The International Journal of Robotics Research,1985,4(2):3?9

22 Salisbury J K,Craig J J.Articulated hands:force control and kinematic issues.The International Journal of Robotics Research,1982,1(1):4?17

23 Huang Zhen,Kong Ling-Fu,Fang Yue-Fa.Parallel Robot Mechanism and Control Theories.Beijing:Machinery Industry Press,1997.183?186 (黃真,孔令富,方躍法.并聯機器人機構學理論及控制.北京:機械工業出版社,1997.183?186)

24 Xiong You-Lun,Ding Han,Liu En-Cang.Robotics.Beijing: Machinery Industry Press,1993.118?128 (熊有倫,丁漢,劉恩滄.機器人學.北京:機械工業出版社,1993. 118?128)

25 Zhang Xin.Optimization of Motion Parameters of a 3-UPS/S Spherical Parallel Mechanism[Master dissertation], Yanshan University,China,2013 (張新.一種3-UPS/S球面并聯機構的運動參數優化研究[碩士學位論文],燕山大學,中國,2013)

26 Cui Bing-Yan,Jin Zhen-Lin.Analysis of statics performance for a novel elbow joint of agricultural robot.Transactions of the CSAE,2011,27(3):122?125 (崔冰艷,金振林.農業機器人新型肘關節的靜力學性能分析.農業工程學報,2011,27(3):122?125)

27 Qing Jian-Xi,Li Jian-Feng,Fang Bin.Drive optimization of Tricept parallel mechanism with redundant actuation.Chinese Journal of Mechanical Engineering,2010,46(5): 8?14 (卿建喜,李劍鋒,方斌.冗余驅動Tricept并聯機構的驅動優化.機械工程學報,2010,46(5):8?14)

28 Feng Zhi-You,Zhang Yan,Yang Ting-Li,Zhang Ce.Inverse dynamics of a 2UPS-2RPS parallel mechanism by Newton-Euler formulation.Transactions of the Chinese Society for Agricultural Machinery,2009,40(4):193?197 (馮志友,張燕,楊廷力,張策.基于牛頓歐拉法的2UPS-2RPS并聯機構逆動力學分析.農業機械學報,2009,40(4):193?197)

李劍鋒北京工業大學機械工程與應用電子技術學院教授.1999年獲北京航空航天大學機器人所博士學位.主要研究方向為機器人,并聯機構與穿戴外骨骼技術.本文通信作者.

E-mail:lijianfeng@bjut.edu.cn

(LI Jian-FengProfessor at the College of Mechanical Engineering and Applied Electronics Technology,Beijing University of Technology.He received his Ph.D.degree from Robotics Institute,Beihang University in 1999.His research interest covers robot,parallel mechanism and wearable exoskeleton technology.Corresponding author of this paper.)

徐成輝北京工業大學機械工程與應用電子技術學院碩士研究生.2013年獲得武漢紡織大學機械工程與自動化學院學士學位.主要研究方向為穿戴外骨骼技術.E-mail:xchde628@163.com

(XU Cheng-HuiMaster student at the College of Mechanical Engineering and Applied Electronics Technology,Beijing University of Technology.He received his bachelor degree from Mechanical Engineering and Automation,Wuhan Textile University in 2013.His main research interest is wearable exoskeleton technology.)

陶春靜國家康復輔具研究中心副教授. 2007年獲中國科學院電氣工程研究所博士學位.主要研究方向為康復設備設計與穿戴外骨骼技術.

E-mail:taochj@gmail.com

(TAO Chun-JingAssociate professor at the National Research Center for Rehabilitation Technical Aids.She received her Ph.D. degree from Institute of Electrical Engineering,Chinese Academy of Sciences in 2007.Her research interest covers rehabilitation equipment design and wearable exoskeleton technology.)

季 潤國家康復輔具研究中心工程師. 2008年獲首都醫科大學學士學位.主要研究方向為康復設備設計與穿戴外骨骼技術.E-mail:jirun@gmail.com

(JI RunEngineer at the National Research Center for Rehabilitation Technical Aids.He received his bachelor degree from Capital Medical University in 2008.His research interest covers rehabilitation equipment design and wearable exoskeleton technology.)

李世才北京工業大學機械工程與應用電子技術學院碩士研究生.2014年獲得哈爾濱理工大學機電學院學士學位.主要研究方向為穿戴外骨骼技術.

E-mail:lishicaijiayou@163.com

(LI Shi-CaiMaster student at the College of Mechanical Engineering and Applied Electronics Technology,Beijing University of Technology.He received his bachelor degree from Mechanical and Electrical Engineering,Harbin University of Science and Technology in 2014.His main research interest is wearable exoskeleton technology.)

張兆晶北京工業大學機械工程與應用電子技術學院碩士.2014年獲北京工業大學大學機械工程與應用電子技術學院學士學位.主要研究方向為穿戴外骨骼技術.E-mail:jmzzj050@sina.com

(ZHANG Zhao-JingMasterstudent at the College of Mechanical Engineering and Applied Electronics Technology,Beijing University of Technology.He received his bachelor degree from College of Mechanical Engineering and Applied Electronics Technology,Beijing University of Technology in 2014.His main research interest is wearable exoskeleton technology.)

A Parallel Ankle Rehabilitation Mechanism and Its Performance Analysis Based on 3-UPS/RRR

LI Jian-Feng1,2XU Cheng-Hui1,2TAO Chun-Jing3JI Run3LI Shi-Cai1,2ZHANG Zhao-Jing1,2

Based on the physiological anatomical structure and movement characteristics analysis of human ankle joint, a 3 degree of freedom(DoF)3-UPS/RRR ankle rehabilitation parallel mechanism is presented.Its three active branched chain inclination arrangement avoids the singular confguration of the mechanism and meets the required ankle rehabilitation workspaces.By means of constraint branches and the moving platform,the mechanism center of rotations matches the patient's ankle center of rotations.Inverse kinematics is solved analytically velocity Jacobian matrix and statics Jacobian matrix are established,and mechanism workspace is coped with.Moreover,in view of Jacobian matrix, kinematics performance and statics performance of the mechanism are analyzed and simulated.The result shows that the mechanism is of favorable operability,fexibility,and stifness characteristics,and its torque transmission is within the specifed workspace.Lastly,inverse dynamics equations of the mechanism are modeled by Newton-Euler formulation; the relationship among driving forces,constraint forces and motion parameters are obtained.A computational example is provided.

Ankle rehabilitation,parallel mechanism,constrained branched chain,torque transmission performance, Newton-Euler

李劍鋒,徐成輝,陶春靜,季潤,李世才,張兆晶.基于3-UPS/RRR的并聯踝關節康復機構及其性能分析.自動化學報,2016,42(12):1794?1807

Li Jian-Feng,Xu Cheng-Hui,Tao Chun-Jing,Ji Run,Li Shi-Cai,Zhang Zhao-Jing.A parallel ankle rehabilitation mechanism and its performance analysis based on 3-UPS/RRR.Acta Automatica Sinica,2016,42(12):1794?1807

2016-02-04 錄用日期2016-09-30

Manuscript received February 4,2016;accepted September 30, 2016

國家自然科學基金(61273342),北京市自然科學基金 (3132005, 3113026)資助

Supported by National Natural Science Foundation of China (61273342),Natural Science Foundation of Beijing(3132005, 3113026)

本文責任編委王衛群

Recommended by Associate Editor WANG Wei-Qun

1.北京工業大學機械工程與應用電子技術學院北京100124 2.北京工業大學北京市先進制造技術重點實驗室北京100124 3.國家康復輔具研究中心北京100176

1.The College of Mechanical Engineering and Applied Electronics Technology,Beijing University of Technology,Beijing 100124 2.Advanced Manufacturing Technology of the Key Laboratory of Beijing Municipality,Beijing University of Technology,Beijing 100124 3.National Research Center for Rehabilitation Technical Aids,Beijing 100176