一類調節強度可變的弱化緩沖算子及其應用研究
劉解放,劉思峰,方志耕
(1.河南科技學院數學科學學院,河南 新鄉 453003;2.南京航空航天大學經濟與管理學院,江蘇 南京 210016)
?
一類調節強度可變的弱化緩沖算子及其應用研究
劉解放1,2,劉思峰1,方志耕1
(1.河南科技學院數學科學學院,河南 新鄉 453003;2.南京航空航天大學經濟與管理學院,江蘇 南京 210016)
在灰色系統緩沖算子公理體系下,根據灰色系統的“新信息優先原理”,構造了一類調節強度可變的弱化緩沖算子,并對其特性進行了研究。針對不同的建模背景,通過調整緩沖算子的參數,可以生成具有不同弱化效果的序列。最后,利用本文提出的緩沖算子,對兩個實際案例進行了建模計算,計算結果表明,這類新的弱化緩沖算子能夠有效提高GM(1,1)模型的預測精度,解決定量預測結果與定性分析結論不符的問題。
緩沖算子;緩沖強度;弱化算子;預測精度
1 引言
灰色系統是通過對原始數據的挖掘、整理來尋求其變化規律的。灰色系統理論認為,盡管客觀系統表象復雜,數據離亂,但它總是有整體功能的,因此必然蘊含某種內在規律,關鍵在于如何選擇適當的方式去挖掘它和利用它[1]。對于沖擊擾動系統預測,模型選擇理論也將失去其應有的功效,因為問題的癥結不在模型的優劣,而是由于系統行為數據因系統本身受到某種沖擊波的干擾而失真。這時候,系統行為數據已不能正確地反映系統的真實變化規律[2],基于此,劉思峰[3-4]教授提出了緩沖算子理論,對原始數據序列經過某種生成,弱化序列的隨機性,使得序列呈現出應有的規律性,減弱沖擊擾動系統的干擾,進而使得到的灰色預測模型更加符合事物的發展變化規律。
為減弱沖擊因素的干擾,劉思峰教授[3]提出了緩沖算子的概念,并構造了一種得到較廣泛應用的實用緩沖算子。黨耀國等學者[5-12]構造了若干個弱化緩沖算子,并對其性質進行了研究。現有的弱化緩沖算子可以對受沖擊因素干擾的系統特征數據進行弱化緩沖,在一定程度上提高了GM(1,1)模型的預測精度。但不足之處在于,上述緩沖算子較少討論緩沖算子的緩沖強度,且都是基于一種固定的緩沖強度,無法根據系統的特點進行緩沖強度的調節,還原系統的真實面貌,這在一定程度上限制了上述弱化緩沖算子的應用。基于此,根據灰色系統的“新信息優先原理”和“最少信息原理”,本文提出一種緩沖強度可以調節的弱化緩沖算子,新提出的弱化緩沖算子只需用到系統的當前信息和最新信息,充分考慮了系統最新信息的重要性,而且,通過調節強度參數,可以使緩沖后的序列更加能夠反映系統的真實運行規律,減弱系統的沖擊擾動,從而可以有效提高GM(1,1)模型的預測精度,可以有效拓展弱化緩沖算子的應用范圍。最后,通過實例驗證了所提出的緩沖算子的有效性和實用性。
2 基本概念
定義1 設系統行為數據序列為X=(x(1),x(2),…,x(n))
(1)若?k=2,3,…,n,x(k)-x(k-1)>0,則稱X為單調增長序列;
(2)若?k=2,3,…,n,x(k)-x(k-1)<0,則稱X為單調衰減序列;
(3)若存在k,k′∈(2,3,…,n),有
x(k)-x(k-1)>0,x(k′)-x(k′-1)<0
則稱X為隨機振蕩序列。設
M=max{x(k)|k=1,2,…,n},m=min{x(k)|k=1,2,…,n}
稱M-m為序列X的振幅。
公理1[3](不動點公理)設X為系統行為數據系列,D為序列算子,則D滿足
x(n)d=x(n)
公理2[3](信息充分利用公理)系統行為數據序列X中的每一個數據都應充分的參與算子作用的全過程。
公理3[3](解析化、規范化公理)任意的x(k),k=1,2,…,n,皆可由一個統一的x(1),x(2),…,x(n)的初等解析式表達。
定義3 稱上述三個公理為緩沖算子三公理,滿足緩沖算子三公理的序列算子稱為緩沖算子。
定義4 設X為原始數據序列,D為緩沖算子,當X分別為增長序列、衰減序列或振蕩序列時,若緩沖序列XD比原始序列X的增長速度(或衰減速度)減小或振幅縮小,則稱緩沖算子D為弱化算子。
定理1[3]設X=(x(1),x(2),…,x(n))為系統行為序列,XD=(x(1)d,x(2)d,…,x(n)d)為其緩沖序列,則有:
(1)X為單調增長序列,D為弱化緩沖算子?x(k)≤x(k)d,k=1,2,…,n。
(2)X為單調衰減序列,D為弱化緩沖算子?x(k)≥x(k)d,k=1,2,…,n。
(3)X為振蕩序列,D為弱化緩沖算子,則
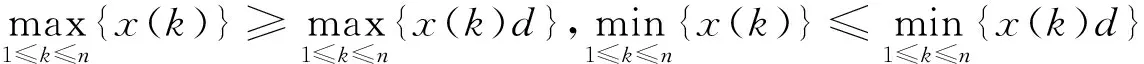
上述定理表明,單調增長序列在弱化算子作用下數據膨脹,單調衰減序列在弱化算子作用下數據萎縮,震蕩序列在弱化算子作用下振幅減小。
3 一類新的弱化緩沖算子的構造
定理2 設X=(x(1),x(2),…,x(n))(x(k)>0),為系統行為序列,XD1=(x(1)d1,x(2)d1,…,x(n)d1)為其緩沖序列,其中:

則當X為單調增長序列、單調衰減序列和震蕩序列時,D1皆為弱化緩沖算子。
證明 不難驗證,D1滿足緩沖算子三公理,顯然D1為緩沖算子,以下證明D1是弱化緩沖算子。
(1)設X為單調增長序列,則:
x(k)d1>x(k)
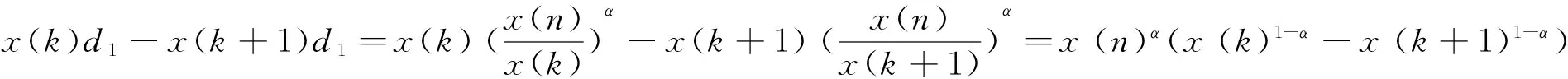
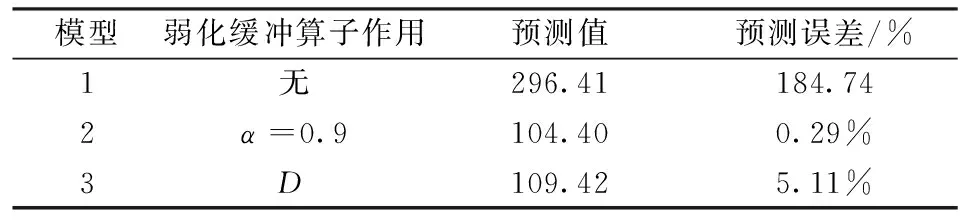
因為0<α<1,所以1-α>0,又因為X是單調增長序列,所以x(k) x(k)d1-x(k+1)d1=x(n)α(x(k)1-α-x(k+1)1-α)<0,這說明緩沖算子D1作用后的序列和原始序列的單調性保持一致。 (2)設X為單調衰減序列,則: x(k)d1 且: 因為0<α<1,所以1-α>0,又因為X是單調衰減序列,所以x(k)>x(k+1),因此: x(k)d1-x(k+1)d1=x(n)α(x(k)1-α-x(k+1)1-α)>0,這說明緩沖算子D1作用后的序列和原始序列的單調性保持一致。 (3)設X為震蕩序列,若: x(M)=max{x(k)|k=1,2,…,n},x(m)=min{x(k)|k=1,2,…,n} 所以,x(M)d1 定理3 設X=(x(1),x(2),…,x(n))(x(k)>0)為系統行為序列,XD2=(x(1)d2,x(2)d2,…,x(n)d2)為其緩沖序列,其中: 則當X為單調增長序列、單調衰減序列時,D2皆為弱化緩沖算子。 證明 不難驗證,D2滿足緩沖算子三公理,顯然D2為緩沖算子,以下證明D2是弱化緩沖算子。 (1)設X為單調增長序列,則: 因此x(k)d2>x(k)。由定理1可知,D2為弱化緩沖算子。 (2)設X為單調衰減序列,則: 因此x(k)d2 從緩沖算子的構造過程可以看出,新的緩沖算子充分的利用了最新的信息x(n),符合灰色系統理論的“新信息優先原理”,同時,由于新的緩沖算子含有調節參數,因此,其緩沖強度可以根據建模的需要進行調節,使得調節后的緩沖算子更加符合系統的發展規律。 實例1 為了驗證新的弱化緩沖算子的作用,以2003-2009年河南省能源消費總量為原始數據來構建預測模型。 表1 2003-2009年河南省能源消費總量 (單位:萬噸標準煤) 本文以2003-2008年河南省能源消費總量的數據序列作為模擬數據,2009年數據序列作為預測數據。計算河南省能源消費總量增長率依次為23.40%,11.86%,11.00%,9.88%,6.38%,4.08%。可以看出,相比之下,2004-2007年的增長速度較快,2008-2009年的增長速度較慢,若直接利用原始數據建立灰色預測模型,則會導致所建立的模型無法準確反映系統的變化情況,所得到的預測結果偏低。為了提高模型的預測精度,需要對原始數據序列進行平滑,以削弱沖擊擾動系統的干擾,凸顯數據的規律性。 因此,以本文所提出的弱化緩沖算子對原始數據序列進行弱化處理,并選擇適當的參數α的值,建立預測模型,并與直接利用原始數據建立的模型進行對比,結果見表2。 表2 弱化緩沖算子作用前后的GM(1,1)模型的計算結果對比 從表2可以看出,當α=0.7的時候,預測相對誤差最小,預測精度為99.33%,隨著α值的減小,算子的弱化效果減弱,隨著α的值增大,算子的弱化效果增強。對于不同的模型,可以調節α的值,以達到最佳的預測效果,也可以借助智能優化算法,如粒子群算法,遺傳算法等尋找最優的參數α的值,以達到最優的預測效果。 實例2以黨耀國[7]中的數據為例,來驗證本文提出的緩沖算子的優越性。原始數據X=(0.33,0.9,10.24,42.24,88.24,104.10).增長率依次為172.73%,1037.78%,312.50%,108.90%,17.97%,序列的變化率呈現出明顯的先快后慢的特點。以前5個數據為模擬數據,以第6個數據為預測數據,直接建模和對于緩沖后的序列建模的計算結果,如表3所示,其中D為黨耀國[7]研究中采用的二階緩沖算子。 表3 弱化緩沖算子作用前后的GM(1,1)模型的計算結果對比 從表3可以看出,經過本文提出的弱化緩沖算子的調節,有效的減少了系統的沖擊擾動,經過緩沖強度的優化,可以使得預測誤差大幅減少。 在已有研究的基礎上,根據灰色系統的“新信息優先原理”,本文提出一種緩沖強度可以調節的弱化緩沖算子,并分析了其性質。以2003年-2009年河南省能源消費總量為原始數據,利用本文構造的弱化算子對原始序列與經過弱化后的數據序列分別進行建模,比較所建模型的預測精度。實例的運算結果表明:(1)經過弱化緩沖算子作用后的數據序列在預測精度上比用原始數據序列預測精度均有顯著提高;(2)通過調節參數α的值,可以調節弱化緩沖算子的弱化效果,使得弱化效果增強或者減弱,以達到最佳的預測效果。針對不同的數據,如何選擇不同的弱化緩沖算子,使得弱化后的序列更加符合系統的發展變化規律,以及如何選擇緩沖算子的階數,都是未來值得研究的課題。 [1] 鄧聚龍.灰理論基礎[M].武漢:華中科技大學出版社,2002. [2] 劉思峰,黨耀國,方志耕,等.灰色系統理論及其應用(第5版)[M].北京:科學出版社2010. [3] Liu Sifeng.The three axioms of buffer operator and their application[J].Journal of Grey System,1991,3(1): 39-48. [4] 劉思峰.沖擊擾動系統預測陷阱與緩沖算子[J].華中理工大學學報1997,25(1): 25-27. [5] 黨耀國,劉斌,關葉青.關于弱化算子的研究[J].控制與決策,2005,20(12): 1332-1336. [6] 黨耀國,劉思峰,米傳民.弱化緩沖算子性質的研究[J].控制與決策,2007,22(7): 730-734. [7] 黨耀國,劉思峰,劉斌,等.關于弱化緩沖算子的研究[J].中國管理科學,2004,12(2): 108-111. [8] 吳正朋,劉思峰,米傳民,等.基于反向累積法的弱化緩沖算子序列研究[J].中國管理科學,2009,17(03):136-141. [9] 謝乃明,劉思峰.弱化緩沖算子的性質與若干實用弱化算子的構造[J].統計與決策,2006,(4):9-10. [10] 崔立志,劉思峰,吳正朋.新的弱化緩沖算子的構造及其應用[J].系統工程理論與實踐,2010,0(3): 484-489. [11] 花玲,謝乃明.政策沖擊影響下中國能源消費預測分析及控制策略[J].中國管理科學,2014,22(07):18-25. [12] 葉璟,李炳軍,劉芳.弱化緩沖算子對GM(1,1)模型的預測效應及適用性[J].系統工程理論與實踐,2014,34(09):2364-2371. [13] Wu Zhengpeng, Liu, Sifeng,Mi Chuanmin, et al.Study on the sequence of weakening buffer operator based on old weakening buffer operator[J].Journal of Grey System,2008,20(3):229-234. [14] Liao Ruijin, Bian Jianpeng, Yang Lijun, et al.Forecasting dissolved gases content in power transformer oil based on weakening buffer operator and least square support vector machine-Markov[J]. Iet Generation Transmission &Distribution,2011,6(2):142-151. [15] Zhou Han,Huang Jiejun, Yuan Yanbin,et al.Prediction of water consumption in hospitals based on a modified grey GM (0,1|sin) model of oscillation sequence: The example of wuhan city[J].Journal Of Applied Mathematics,2014:1-7. [16] Luo Dang, Wang Xia.The construction of new weakening buffer operators and their application[J].Grey Systems: Theory and Application,2011,1(2): 148-157. [17] Wei Yang, Kong Xinhai, Hu Dahong.A kind of universal constructor method for buffer operators[J].Grey Systems: Theory and Application,2011,1(2):178-185. [18] 劉永菲,張輝,解忠誠.一類新弱化緩沖算子的構造[J].中國傳媒大學學報(自然科學版),2014,21(03): 51-55,41. A Class of New Weakening Buffer Operators Whose Adjustable Intensity Can be Changed and Their Applications LIU Jie-fang1,2,LIU Si-feng1,FANG Zhi-geng1 (1.School of Mathematical Science, Henan Institute of Science and Technology, Xinxiang 453003,China;2.College of Economics and Management, Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China) buffer operator; buffer intensity; weakening operator; forecast precision 2014-10-29; 2015-11-09 國際人才引進計劃資助項目(FP7-PIIF-GA-2013-629051);國家自然科學基金資助項目(91324003, 71171113,71401051);國家自然科學基金與英國皇家學會國際合作交流項目(71111130211);國家科技重大專項(2009ZX11002);國家社會科學基金資助重點項目(12AZD102) 簡介:劉解放(1980-),男(漢族),河南周口人,河南科技學院數學科學學院講師,博士,研究方向:灰色系統理論、裝備研制管理等,E-mail:liujf101@126.com. N94 A 1003-207(2016)08-0172-05 10.16381/j.cnki.issn1003-207x.2016.08.021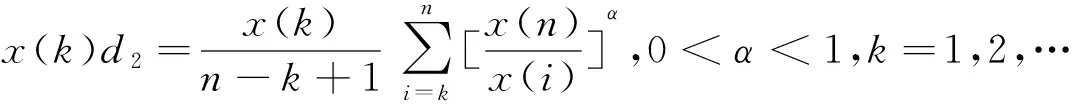
4 實例分析


5 結語


