基于PRSM法的噴水織機打緯機構剛體動力學平衡優化

毛 瑩，孫志宏，江長云，許亞紅，RAHMAN Habibur

(東華大學 機械工程學院，上海 201620)

基于PRSM法的噴水織機打緯機構剛體動力學平衡優化

毛 瑩，孫志宏，江長云，許亞紅，RAHMAN Habibur

(東華大學 機械工程學院，上海 201620)

打緯機構動平衡問題的研究對解決織機存在較大震動和噪聲的現狀有重要意義.為了更好地解決打緯機構在慣性打緯時對機架產生的震動力和震動力矩，在保證打緯工藝的條件下，采用一種新方法——部分冗余伺服電機(PRSM)法，結合配重法對噴水織機的四連桿打緯機構進行剛體動力學平衡優化，驗證了部分冗余伺服電機法對四連桿打緯機構剛體動力學平衡的有效性，為該方法在其他連桿機構中的應用提供參考.

打緯機構；部分冗余伺服電機法；動力學；平衡

打緯機構作為織機的五大機構之一，其性能直接影響著織機的整機性能. 四連桿打緯機構各構件加速度周期性變化引起的慣性力和慣性力矩作用在機架上產生震動力和震動力矩，它們是引起織機震動和噪聲的主要原因之一[1]. 因此，降低慣性打緯機構在打緯時對機架產生的震動力和震動力矩，已成為實際生產中面臨的主要問題.

目前，對四連桿打緯機構進行震動平衡的方法主要是配重法、調整構件尺寸以及附加彈性元件等. 近幾年，文獻[24]提出了部分冗余伺服電機法(簡稱PRSM法)，經研究其對剛性和彈性四連桿、五連桿機構的動力學平衡有較好的優化效果. 因此，本文采用PRSM法并結合傳統的配重法，在不考慮彈性的情況下，以RFJW10智能型噴水織機的四連桿打緯機構為研究對象進行動力學平衡優化.

1 機構的動力學分析

四連桿打緯機構一般由偏心曲軸、牽手、筘座及筘座腳4個部分組成，在本文中將筘座及筘座腳作為一個整體進行處理. 圖1和2分別為四連桿打緯機構的機構簡圖以及構件的受力分析圖，其中：S1、S2、S3為各構件質心；m1、m2、m3為各構件質量；θ1、θ2、θ3為各構件質心與桿長的夾角；l1、l2、l3、l4為各構件長度；Fr21x、Fr21y、Fr41x、Fr41y、Fr32x、Fr32y、Fr43x、Fr43y為各構件的運動副受力；F1x、F1y、F2x、F2y、F3x、Fr3y為各構件質心所受慣性力；Mb為輸入轉矩.

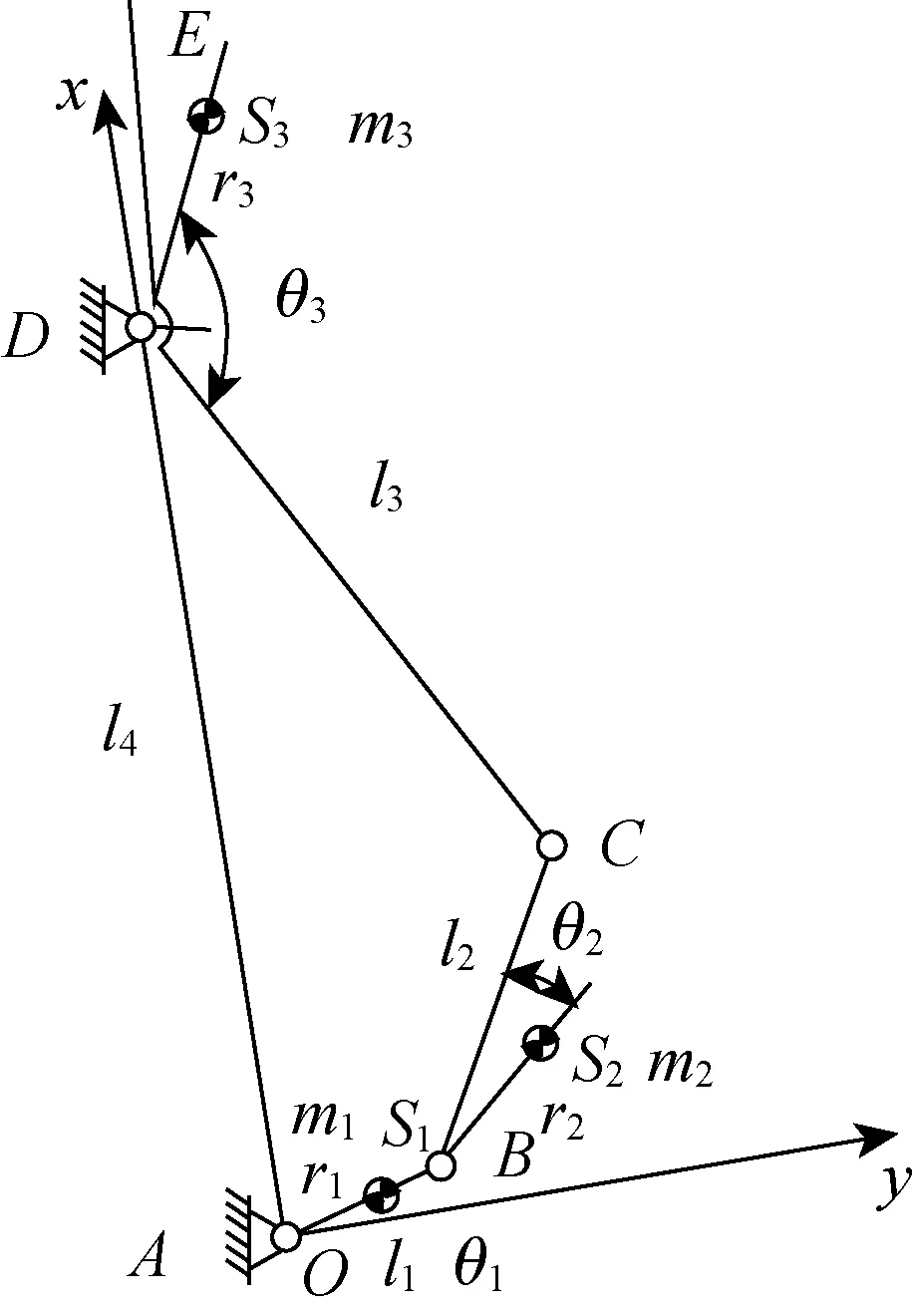
圖1 四連桿打緯機構簡圖Fig.1 Four-link beating-up mechanism sketch

圖2 構件的受力分析圖Fig.2 Stress analysis of parts

根據達朗貝爾原理可知，各構件所受諸力與其所受慣性力組成平衡力系[5 - 6]，因此，分別對打緯機構各桿件的質心點取矩，可以寫出平衡方程式，其基本形式為

(1)

其中：Fx，Fy分別為各運動副受力和各構件所受慣性力在x軸、y軸方向上的合力；M為各構件在質心處所受的合力矩.

為便于Matlab編程求解，將以上線性方程組表達成矩陣形式的平衡方程：

C*FR=D

(2)

式中：C為系數矩陣；FR為未知力列陣；D為已知力列陣. 其中

(3)

其中：xS1、yS1、xS2、yS2、xS3、yS3為各構件質心的坐標；xA、yA、xB、yB、xC、yC、xD、yD為各構件運動副的坐標.

FR=[ MbFr14xFr14yFr12xFr12y

(4)

D=[ -M1-F1x-F1y-M2-F2x

-F2y-M3-F3x-F3y]T

(5)

機構的震動力可表示為

(6)

取鉸鏈點A作為對象，則打緯機構相對于鉸鏈點A的震動力矩可以表示為

Msh=-(Fr43y·l4+Mb)

(7)

2 打緯機構的配重法平衡

任意一個平面四桿機構，其總質心的位置可以

表示為

(8)

當平面四桿機構總質心保持靜止(即rC為常數)時，其震動力能夠達到完全平衡.因此，根據配重法對打緯機構進行平衡，四連桿打緯機構在配重前后的參數如表1所示.

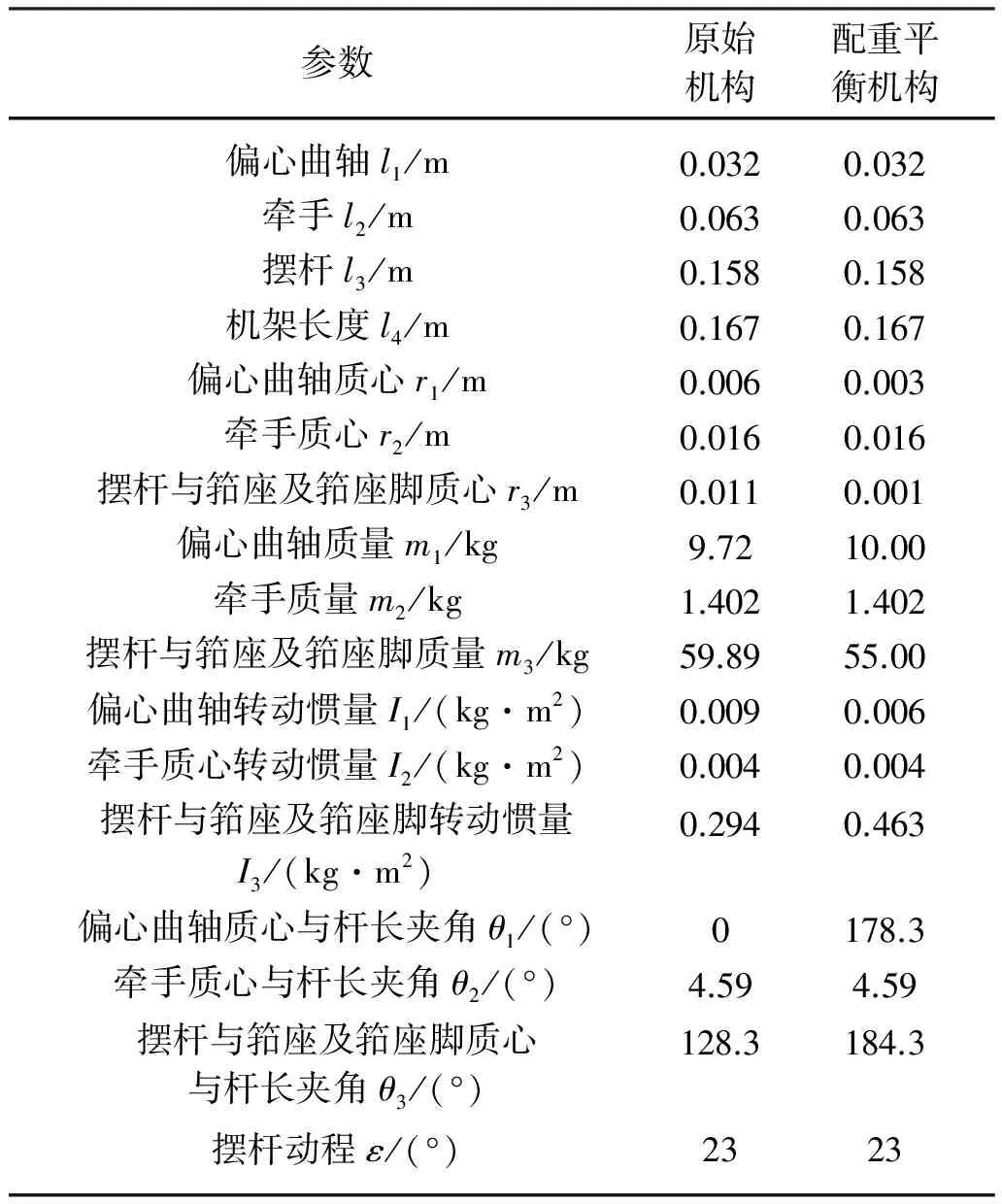
表1 四連桿打緯機構參數Table 1 Parameters of four-link beating-up mechanism

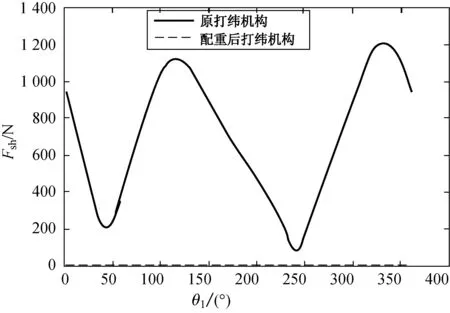
(a) 震動力

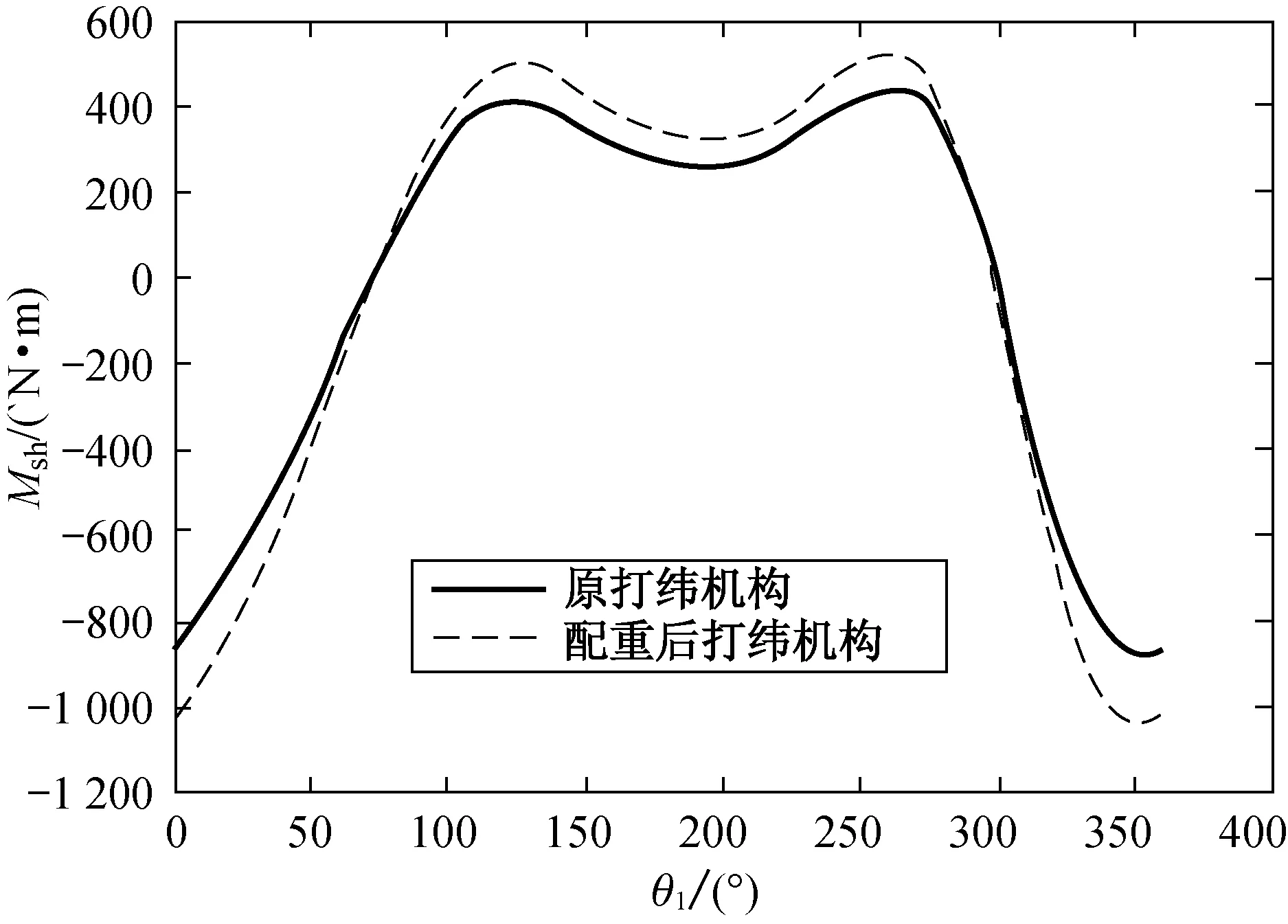
(b) 震動力矩圖3 配重前后震動力圖及震動力矩圖Fig.3 Shaking force and shaking moment before and after counter weight

利用Matlab計算得到配重法優化前后打緯機構的震動力和震動力矩變化規律，曲線分別如圖3所示.經過配重法平衡后的震動力有較大的改善，幾乎為零(圖3(a))；但震動力矩有所增大(圖3(b))，產生這種現象主要原因是經配重后，桿件的轉動慣量有所增加，導致了震動力矩的增大，因此本文將在此基礎上，再利用PRSM法對機構的震動力矩進行平衡.

3 利用PRSM法對打緯機構的平衡

RFJW10智能型噴水織機打緯機構的幾何參數如表1所示，設織機轉速n=800 r/min，周期T=0.075 s.對打緯機構進行運動學分析可得，打緯時鋼筘的角加速度為α=2.2×103rad/s2.同時根據噴水織機打緯的工藝要求可知，主軸一周內織機各部件的運動關系如表2所示.

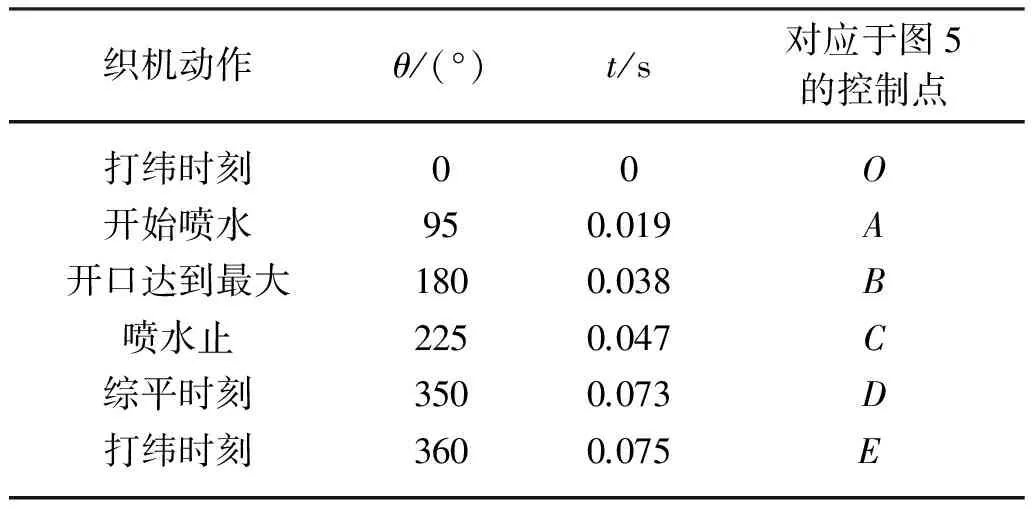
表2 噴水織機各構件運動配合表Table 2 Motion coordination of different mechanisms in the water-jet loom

注：主軸轉角θ是指織機各動作所對應的主軸轉動角度；時間t是指一個周期內主軸轉角所對應的時間點；控制點代表的是電機運動曲線上與主軸轉角對應的點(如圖4所示).

為保證產生足夠大的打緯力并滿足織機三大運動(開口、引緯、打緯)之間的運動配合要求，利用PRSM法對打緯機構進行動平衡優化時的約束條件(1)打緯時刻鋼筘的角加速度達到α=2.2×103rad/s2；(2)伺服電機轉角(qi/(°)，i=0, 1,…， 5)曲線必須經過表2中所列控制點.如圖4所示，虛線表示常速電機的轉角曲線，實線代表的是滿足約束條件的伺服電機的轉角曲線.

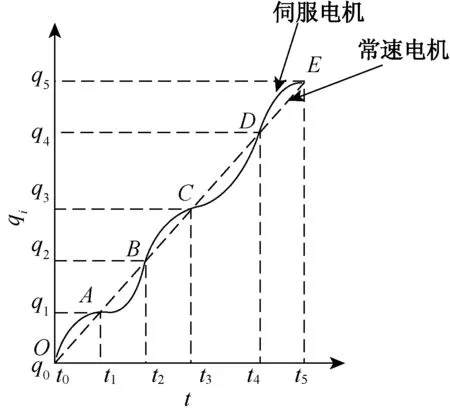
圖4 伺服電機轉角曲線Fig.4 Servo motor rotation curve

通過配重法已經使打緯機構在運動過程中產生的震動力得到了有效的平衡.當震動力完全平衡后，機構的震動力矩為力偶矩.因此取優化目標函數：

(9)

在確定約束條件和優化目標函數的條件下，利用Matlab中的遺傳算法，采用概率化尋優方法，自適應地在全局范圍內尋找設計變量，以獲得目標函數的最優解.

文獻[2]中采用了式(10)～(12)所示的3種多項式曲線作為伺服電機轉角曲線，并取得了較好的優化效果，因此本文中繼續采用此3種多項式曲線，并根據控制點之間的特性，在同一個周期將這3種多項式曲線規律進行組合，同時保證各規律在控制點處分別滿足一階導數連續，二階導數連續和三階導數連續.各段中伺服電機轉角曲線的規劃如表3所示.

五次多項式:

q1(t)=a0+a1t+…+a4t4+a5t5

(10)

七次多項式:

q2(t)=a0+a1t+…+a6t6+a7t7

(11)

九次多項式:

q3(t)=a0+a1t+…+a8t8+a9t9

(12)

其中:a0， a1，…， a9為需要通過GA求得的當目標函數最小值時的多項式轉角曲線系數.

表3 伺服電機轉角曲線規劃Table 3 Planning for the servo motor rotation curve

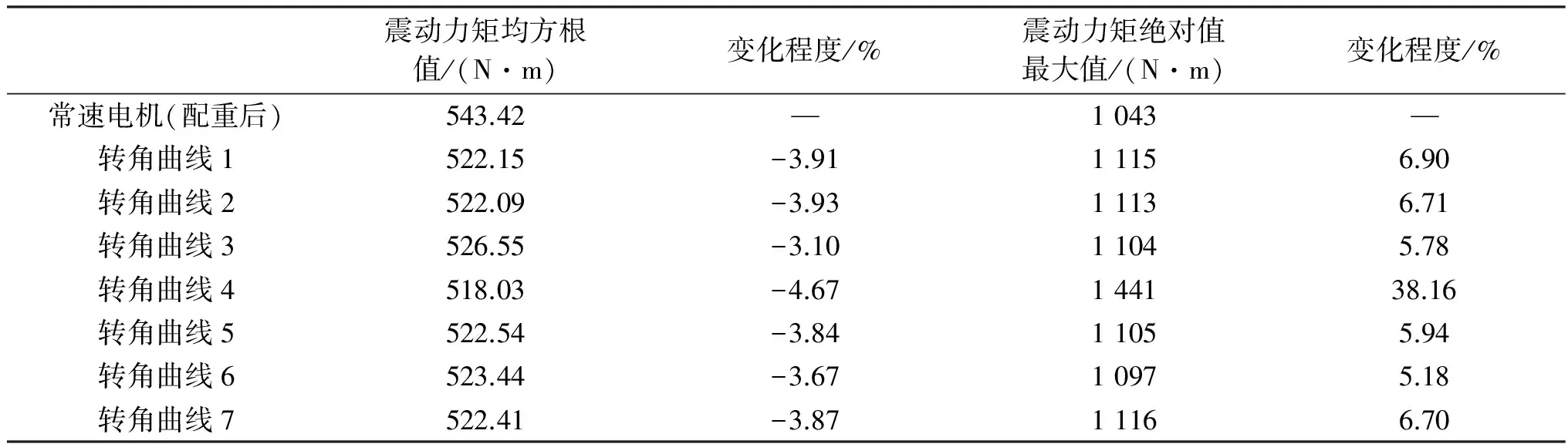
表4 打緯機構震動力矩平衡優化效果Table 4 Optimization results of the beating-up mechanism’s shaking moment

經Matlab優化，震動力矩Msh的平衡情況如圖5所示.表4是打緯機構震動力矩平衡優化效果.

圖5 震動力矩的平衡情況Fig. 5 Shaking moment balancing

從圖5和表4中可以看出：

(1)對于優化目標OF而言，7種伺服電機轉角曲線對打緯機構動平衡優化均有效果，其中轉角曲線4的優化效果最好，震動力矩的均方根值從543.42 N·m下降到518.03 N·m，下降了4.67%；

(2)對于7種伺服電機轉角曲線，優化后震動力矩絕對值的最大值都有所增大，其中轉角曲線4的增幅最大，從1 043N·m增大到1 441N·m，上升了38.16%，產生這種現象的原因是優化過程中，需要保證打緯力足夠大的要求，且震動力矩最大值的點出現在打緯時刻附近，此時震動力矩的增大利于慣性打緯.

綜上可得，轉角曲線4(9次多項式3階連續)對打緯機構動平衡的優化效果較其他轉角曲線好，PRSM法對打緯機構震動力矩的平衡有效.

4 結 語

本文首次將PRSM法應用于噴水織機打緯機構的震動平衡研究. 在建立了動力學模型的基礎上，先采用配重法對打緯機構進行震動力的完全平衡，然后利用PRSM法對震動力矩進行優化. 通過遺傳算法求得7種伺服電機轉角曲線，將這7種運動規律下打緯機構的震動力矩與勻速電機驅動下的情況進行對比可知，PRSM法對打緯機構的震動平衡是有效的.由于打緯機構震動力的完全平衡在工程實際中的實現有難度，因此，在后續的研究中，將PRSM法應用于震動力部分平衡的打緯機構上，以震動力和震動力矩均方根的加權值為優化目標進行優化，也取得了較好的優化效果.

本文用PRSM法對打緯機構進行動平衡優化后，打緯機構的震動力矩仍有些許震蕩，后續可以研究不同的伺服電機轉角規律，以獲得更好的效果.

[1] 祝章琛, 范辰五. 高速織機四桿打緯機構的優化平衡[J]. 中國紡織大學學報, 1988,14(5): 5966.

[2] 張兵. 一種新的機電一體化機構動力學平衡方法：冗余伺服電機法的研究與應用[D].上海：東華大學機械工程學院, 2011.

[3] SUN Z H, ZHANG B, HUANG J, et al. On a mechatronics approach to balancing of robotic mechanisms: Redundant servo motor [C]// Proceedings of International Conference on Advanced Mechatronics(ICAM2010), 2010,Osaka, Japan: 675680.

[4] SUN Z H, ZHANG B, CHENG L, et al. Application of the redundant servomotor approach to design of path generator with dynamic performance improvement[J]. Mechanism and Machine Theory, 2011, 46(11): 17841795.

[5] 韓建友. 高等機構學[M]. 北京: 機械工業出版社, 2004.

[6] 劉家強, 張兵, 孫志宏，等. 基于冗余伺服電機的平面四連桿機構震動平衡[J].東華大學學報(自然科學版), 2012, 38(5): 592596.

[7] 歐玉俊, 孫志宏, 章文俊. 基于冗余伺服電機法的彈性連桿機構的平衡[J]. 機械科學與技術, 2012,31(9): 14541457.

[8] 楊元福, 孫志宏, 章文俊. 基于冗余伺服電機法對含外負載的剛性連桿機構的動力學平衡研究[J].機械科學與技術, 2014, 33(12): 17761780.

Dynamic Balancing Optimization of Rigid Beating-up Mechanism on the Water-Jet Loom Based on the Partial Redundant Servo Motor Method

MAOYing,SUNZhi-hong,JIANGChang-yun,XUYa-hong,RAHMANHabibur

(College of Mechanical Engineering, Donghua University, Shanghai 201620, China)

The dynamic balancing study of the beating-up mechanism has a significant meaning in solving the presence status that looms have large vibration and noise. In order to eliminate the shaking force and shaking moment produced by the inertia force of the beating-up mechanism of a loom, a new approach-partial redundant servo motor (PRSM) method, combined with the counter-weight approach, was applied to do the dynamic balancing optimization on beating-up mechanism. The results verify the validity of PRSM method and offer the reference for using it in other mechanisms.

beating-up mechanism; partial redundant servo motor(PRSM)method; dynamics; balancing

16710444 (2016)060889-05

20150924

毛 瑩(1992—)，女，江西南昌人，碩士研究生，研究方向為機械設計及理論.E-mail:yingmying@126.com 孫志宏(聯系人)，女，教授，E-mail:zhsun@dhu.edu.cn

TH 112.1

A