廣義指數分布下區間刪失數據貝葉斯回歸分析
李 群, 董小剛, 王純杰, 趙 波
(長春工業大學 基礎科學學院, 吉林 長春 130012)
廣義指數分布下區間刪失數據貝葉斯回歸分析
李 群, 董小剛, 王純杰*, 趙 波
(長春工業大學 基礎科學學院, 吉林 長春 130012)
研究了在兩參數廣義指數分布下的區間刪失壽命時間的貝葉斯回歸分析模型。生存時間在服從廣義指數分布的情況下,假定形狀參數的先驗分布來自伽馬分布,建立了尺度參數與生存時間貝葉斯回歸模型,從而得到生存時間的變化。選取MCMC算法對參數進行估計,并運用R軟件進行了模擬。
廣義指數分布; 區間刪失; 貝葉斯回歸; MCMC算法
0 引 言
在可靠性壽命試驗中,兩參數廣義指數分布可簡稱廣義指數分布或GE分布。作為指數分布的推廣,由于廣義指數分布對于刪失時間數據有很好的分析效果,而且還可以作Gamma分布和Weibull分布的替代分布,因而在壽命試驗和可靠性工程中有著重要的應用[1-2]。壽命數據分析已經成為航空、工程、醫學和生物科學等多個領域中統計學家和實際工作者十分關心的一個問題,因此,對廣義指數分布的研究有著十分重要的實際意義。同時,在生存分析中也經常研究感興趣的時間與哪些因素有密切的關系,也會研究不同的藥物類型中,哪種藥物對于患者更有效果等。文中將通過建立貝葉斯回歸模型來進行研究感興趣的時間與相關因素的關系及影響[3]。
李榮[4]于2006年給出了一篇刪失實驗壽命的貝葉斯威布爾生存回歸模型,建立了威布爾分布下關于參數λ的回歸模型,并給回歸系數賦予先驗分布。在刪失壽命實驗的條件下,給出了貝葉斯威布爾回歸模型的似然函數,基于Gibbs抽樣得出參數的后驗分布,利用WinBUGS軟件包求解威布爾回歸模型的貝葉斯估計的過程。朱惠明[5]等于2007年給出了刪失試驗壽命的貝葉斯生存極值回歸模型,同樣引入參數λ的協變量,并建立了貝葉斯回歸模型,用MCMC方法和Gibbs抽樣獲得參數后驗分布,同樣利用WinBUGS軟件包求解極值回歸模型的貝葉斯估計的過程。Upadhyay[6]發表了基于Gibbs抽樣下對數正態回歸的后驗分析,分別建立對數正態分布的均值、方差兩個參數關于協變量影響的貝葉斯回歸模型。Puja Makkar[7]給出了頭頸癌在對數正態模型下的貝葉斯生存分析,在不知道先驗信息的情況下,采用Gibbs抽樣的方法得到參數的后驗分布,并分析不同的治療方案對患頭頸癌患者壽命的影響。
廣義指數分布是由Gupta R D和Kundu D于1999年提出的。此外Gupta R D[8-9]等給出了廣義指數分布的一些統計推斷的性質。Kundu D[10]等于2008年給出了廣義指數的貝葉斯估計的相關理論。此外,郭環[11]研究了兩參數廣義指數分布的一些參數估計方法和優良性質,給出了在一定條件下兩個參數的貝葉斯估計。但是上述文獻均沒有涉及廣義指數分布的貝葉斯生存回歸模型。
MCMC方法是一種簡單易行、廣泛應用的計算隨機模擬方法。該方法的核心思想是構建一個概率轉移矩陣,建立一個以分布π(x)為平穩分布的Markov鏈,得到π(x)的樣本,通過隨機抽樣得到的樣本就可以進行各種統計推斷和估計[12]。MCMC方法中最常用的一種方法是Metropolis-Hastings,該方法最早由Metropolis于1953年給出的,后來Metropolis的算法由Hastings改進,合稱為M-H算法[13-14]。M-H算法是MCMC的基礎方法,由M-H算法演化出了許多新的抽樣方法,包括目前在MCMC中最常用的Gibbs抽樣也可以看做M-H算法的一個特例[15]。
1 符號描述和模型介紹
文中主要研究的是區間刪失下的廣義指數分布模型的建立及貝葉斯回歸分析的應用。下面假設第i個個體滿足以下關系:
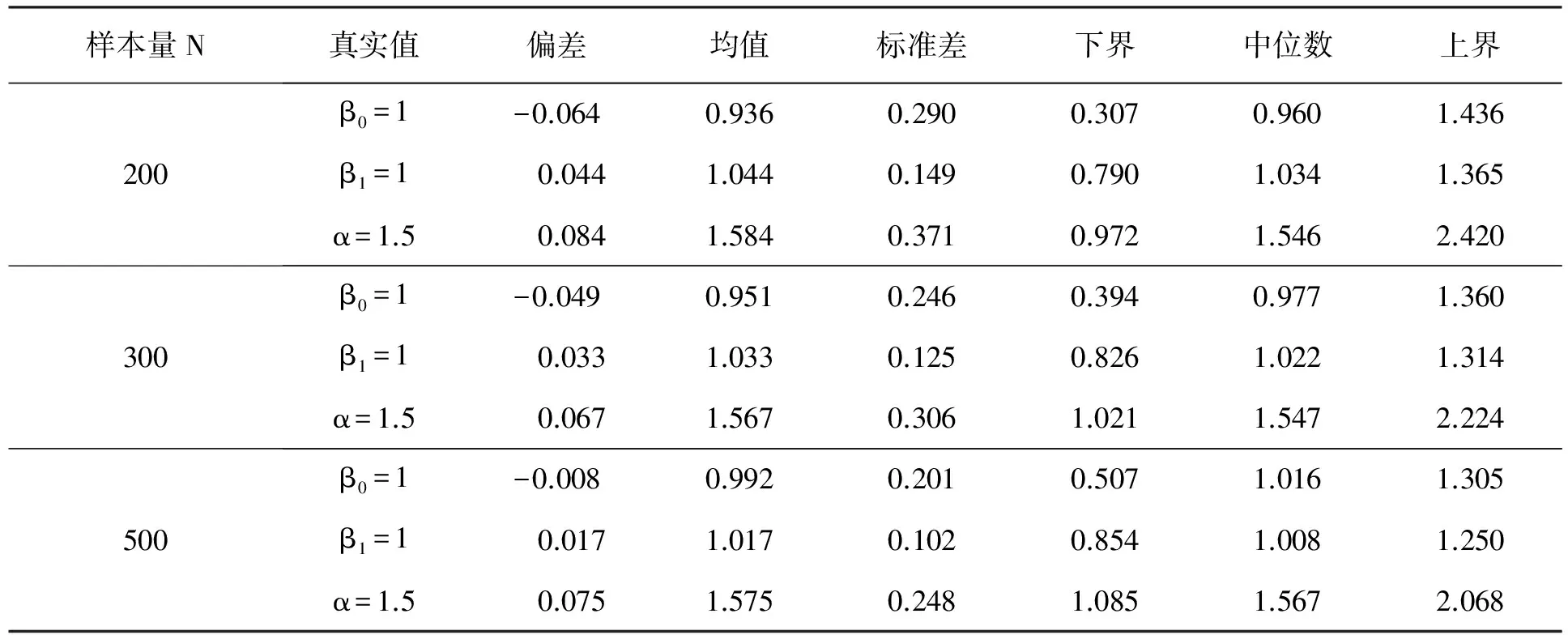
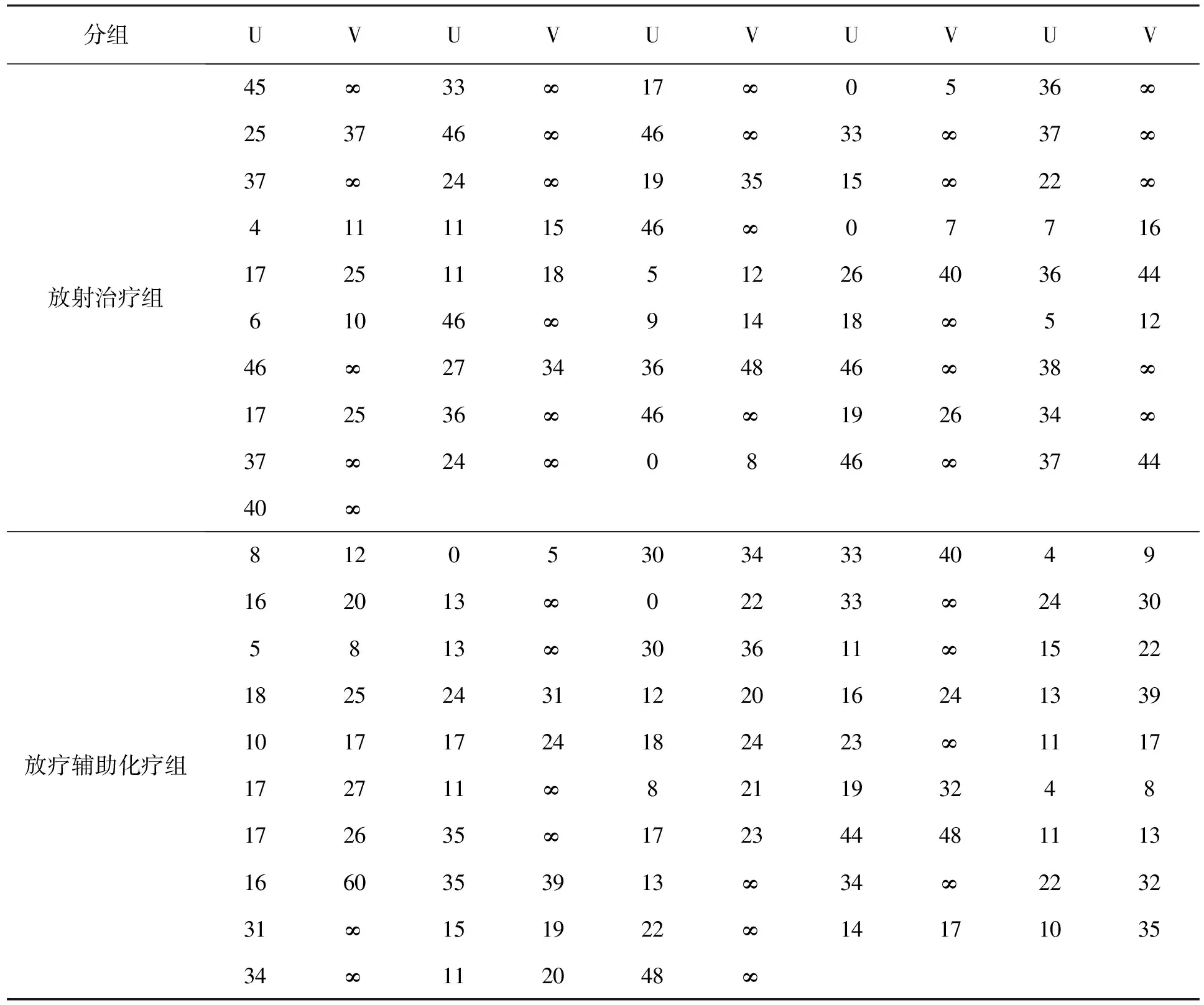
假定每個個體都可以觀測兩次,其中U、V代表兩個隨機變量,并且以概率1滿足U 文中采用的是廣義指數分布對區間刪失數據進行建模[8-9]。廣義指數分布的密度函數為: (1) 其分布函數為: (2) 生存函數為: (3) 風險函數為: (4) 式中: α----形狀參數; λ----尺度參數。 形狀參數為α,尺度參數為λ的廣義指數分布記為GE(α,λ)。 其對應的全數據的似然函數為: (5) 文中研究的是區間刪失情況下的貝葉斯回歸模型,則區間刪失情況下的似然函數為: (6) 故區間刪失數據的對數似然函數可以表示為: (7) 接下來建立貝葉斯層次模型如下: (8) α~gamma(1,0.001) 其中,λi指每個個體生存時間所服從的廣義指數分布的尺度參數,βj,j=0,1,…,m的先驗分布為正態分布,α的先驗分布為gamma分布。 這樣就可以建立起區間刪失數據的廣義指數分布貝葉斯回歸模型。接下來可根據貝葉斯層次模型寫出后驗的聯合密度函數,即后驗似然函數[3,16]為: (9) 故得到后驗對數似然函數為: (10) 接著,運用MCMC算法對參數進行估計。 用數值模擬過程來評價文中建立的模型性能,給出模擬步驟如下: 1)產生來自均勻分布U[-2,2]的N個獨立同分布的x1,x2,…,xN。 2)設定β0=1,β1=1,α=1.5,并令λi=exp(β0+β1xi)。 3)產生N個服從廣義指數分布的失效時間T,形狀參數α=1.5,尺度參數λi=exp(β0+β1xi)。 4)產生N個服從參數為θ1=6的指數分布的第一次觀測時間U,產生N個服從參數為θ2=0.2指數分布的第二次觀測時間V,并滿足U 5)比較U、V和失效時間T的大小關系,若T 6)給出β和α的先驗分布。并寫出先驗似然函數(LL)和后驗似然函數(LP)。 7)應用MCMC算法估計參數β和α。 按照上述算法步驟,循環500次計算出待估參數β和α的均值和方差。樣本量設定為N分別為200、300、500,模擬結果見表1。 表1 樣本量為200,300,500的模擬結果 由表1 可以看出,在樣本量不同,且左刪失比例約為0.2,右刪失比例約為0.4的情況下,模擬參數的估計值較真值偏差較小,能夠給出對應參數較好的估計結果,并且精度會隨著樣本量的增加而增加,樣本標準差也會隨著樣本量的增加而減小。由此可見,該模型用來進行后驗估計是可行的。在算法的選擇上也可采用其他的算法進行估計。 對一個實際數據例子進行研究分析,選取的數據是1976年到1980年之間在波士頓進行乳腺癌早期治療的回顧性研究數據。該數據由Finkelstein和Wolfe在1985年展現出來,數據是由94位病人組成,其中分為給予放射性治療組(RT)和放射性療法加輔助性化學治療組(RCT)。放射治療組共計46位病人,放療加輔助化療組共有48位病人[17]。 在研究過程中,病人每4~6個月隨訪一次,然而,病人的實際訪問時間不同,每個病人的兩次隨訪時間也是不同的。在就診過程中醫生會根據乳腺收縮程度來評估病人情況。這項研究的目的是為了比較這兩組治療方式對患者的治療效果,看放療輔助化療方法是否可以提高患者的無復發率和總的生存率。但是有一些實驗和臨床證據表明,化療加劇了正常組織對放射治療的急性反應。這個數據包含了關于乳腺收縮的信息,但是沒有精確的觀測時間。這里有38例患者在研究期內沒有明顯的乳腺收縮,所以這部分觀測設定為右刪失數據,即這個區間觀測沒有右側端點。對于其他患者,觀測時間的時間間隔代表著在這段時間內發生過乳腺收縮。觀測時間的左端點是從第一次診所就診時間開始,到最后一次就診時發現乳腺收縮截止。例如,觀測到的(6,10]表示在第6個月隨訪時患者未出現乳腺收縮,但是在下一次隨訪,即第10個月時,患者出現了乳腺收縮。乳腺收縮情況出現在第6個月至第10個月兩次隨訪之間,但精確的時間未知。所以我們用區間的刪失時間數據來描述乳腺收縮。將這組數據進行詳細地分析估計,觀測數據見表2。 在進行數據分析的過程中,若第i個病人屬于放射治療組,定義協變量xi=0;若第i個病人屬于放療輔助化療組,定義協變量xi=1,并且假定乳腺癌發作時間服從廣義指數分布。估計結果見表3。 通過表3的實驗結果可以求出 λ=exp(-15.873x) 可以判斷出:當病人屬于放射治療組時,λ=1;當病人屬于放療輔助化療組時,0<λ<1。從而根據生存函數可以判斷出,放療輔助化療方法可以提高患者的無復發率和總的生存率。 表2 乳腺癌觀測數據 表3 乳腺癌數據估計結果 在貝葉斯框架下建立了服從廣義指數分布的生存時間的尺度參數同影響生存時間的相關因素之間的回歸模型,并給出后驗似然函數,采用MCMC方法對后驗似然函數進行求解最大值,同時解出了待估參數。并對該模型進行了模擬,模擬效果較好。并將該方法應用到乳腺癌數據例子中,結果表明,放射療法輔助化療方法對于提高患者的總的生存率有著一定的效果。 [1]GuptaRD,KunduD.Exponentiatedexponentialfamily;analternativetogammaandweibulldistributions[J].BiometricalJournal,2001,43(1):117-130. [2] Gupta R D, Kundu D. Generalized exponential distribution: different method of estimations[J]. Journal of Statistical Computation and Simulation,2001,69(4):315-337. [3] Ibrahim J G, Chen M H, Sinha D. Bayesian survival analysis[M]. New York: John Wiley & Sons Ltd.,2005. [4] 李榮,朱慧明.刪失試驗壽命的貝葉斯威布爾生存回歸模型[J].統計與決策,2006(24):20-22. [5] 朱慧明,李榮,方博文.刪失試驗壽命的貝葉斯生存極值回歸模型[J].系統工程與電子技術,2007,29(11):1988-1990. [6] Upadhyay S K, Peshwani M. Posterior analysis of lognormal regression models using the Gibbs sampler[J]. Statist. Papers,2008,49:59-85. [7] Puja Makkar, Puneet K, Srivastava R S Singh, et al. Bayesian survival analysis of head and neck cancer data using lognormal model[J]. Communication in Statistics-Theory and Methods,2014,43(2):392-407. [8] Gupta R D, Kundu D. Generalized exponential distributions[J]. Australian and New Zealand Journal of Statistics,1999,41(2):173-188. [9] Gupta R D, Kundu D. Generalized exponential distributions: statistical inferences[J]. Technical Report, The University of New Brunswick, Saint John.,1999,41(3):111-115. [10] Kundu D, Gupta R D. Generalized exponential distribution: bayesian estimations[J]. Computational Statistics & Data Analysis,2008,52(4):1873-1883. [11] 郭環.兩參數廣義指數分布的參數估計與數值模擬[D].武漢:華中科技大學,2013. [12] 黃小艷.MCMC方法分析[J].中國市場,2015(14):185-186. [13] Metropolis N, Rosenbluth A W, Rosenbluth M N, et al. Equation of state calculations by fast computing machines[J]. The Journal of Chemical Physics,1953,21(6):1087-1092. [14] Hastings W K. Monte carlo sampling methods using markov chains and their applications[J]. Biometrika,1970,57(1):97-109. [15] Geman S, Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1984(6):721-741. [16] Bernardo J, Smith A. Bayesian theory[M]. West Sussex: John Wiley & Sons.,2000. [17] Finkelstein D M, Ra W. A semiparametric model for regression analysis of interval-censored failure time data[J]. Biometrics,1985,41(4):933-945. Bayesian survival regression analysis of interval censored data with generalized exponential Model LI Qun, DONG Xiaogang, WANG Chunjie*, ZHAO Bo (School of Basic Sciences, Changchun University of Technology, Changchun 130012, China) Bayesian regression analysis model of interval censored lifetime under two-parameter Generalized Exponential is studied. Provided that the lifetime comes from generalized exponential distribution, and the prior distribution of shape parameter derives from the gamma distribution, the Bayesian regression model influenced by scale parameter and survival time is established to obtain the variation of lifetime. MCMC algorithm is used to estimate the parameters, and R software is used for simulation. generalized exponential distribution; interval censored; bayesian regression; MCMC algorithm. 2016-07-19 國家自然科學基金青年基金項目(11301037); 國家自然科學基金資助項目(11571051); 吉林省教育廳“十三五”規劃項目(2016317) 李 群(1991-),女,漢族,山東菏澤人,長春工業大學碩士研究生,主要從事生存分析方向研究,E-mail:liqun91@live.com. *通訊作者:王純杰(1978-),女,漢族,遼寧遼陽人,長春工業大學副教授,博士,主要從事數理統計、生存分析方向研究,E-mail:wangchunjie@ccut.edu.cn. 10.15923/j.cnki.cn22-1382/t.2016.6.16 O 212.4 A 1674-1374(2016)06-0597-06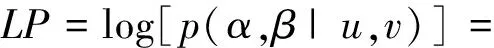
2 數值模擬
3 實證分析

4 結 語

