解開函數及其圖像的面紗
馬愛平
函數及其圖像是初中數學的核心知識,是中考的重點內容,常考考點主要有:
考點1 直角坐標系與點的坐標特征
例1 (2016·甘肅)已知點P(0,m)在y軸的負半軸上,則點M(-m,-m+1)在( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】因為點P(0,m)在y軸的負半軸上,所以m<0,所以-m>0,-m+1>0,所以點M在第一象限,故選擇A.
【點評】解決這類問題要掌握點的橫、縱坐標的取值與點所在象限(或坐標軸)的對應關系以及點的坐標特征.
考點2 確定函數自變量的取值范圍
例2 (2016·四川內江)在函數y=[x-3x-4]中,自變量x的取值范圍是( ).
A.x>3 B.x≥3
C.x>4 D.x≥3且x≠4
【解析】由題意,得x-3≥0且x-4≠0,∴x≥3且x≠4,故選擇D.
【點評】求函數自變量的取值范圍就是確定使函數解析式有意義的自變量的取值.此外,要注意“或”與“且”的區別.
考點3 用函數圖像描述有關信息
例3 (2016·山東菏澤)小明騎自行車上學,開始以正常速度勻速行駛,但行至中途自行車出了故障,只好停下來修車,車修好后,因怕耽誤上課,加快了騎車速度,圖1是小明離家后他到學校剩下的路程S關于時間t的函數圖像,那么符合上面行駛情況的圖像大致是( ).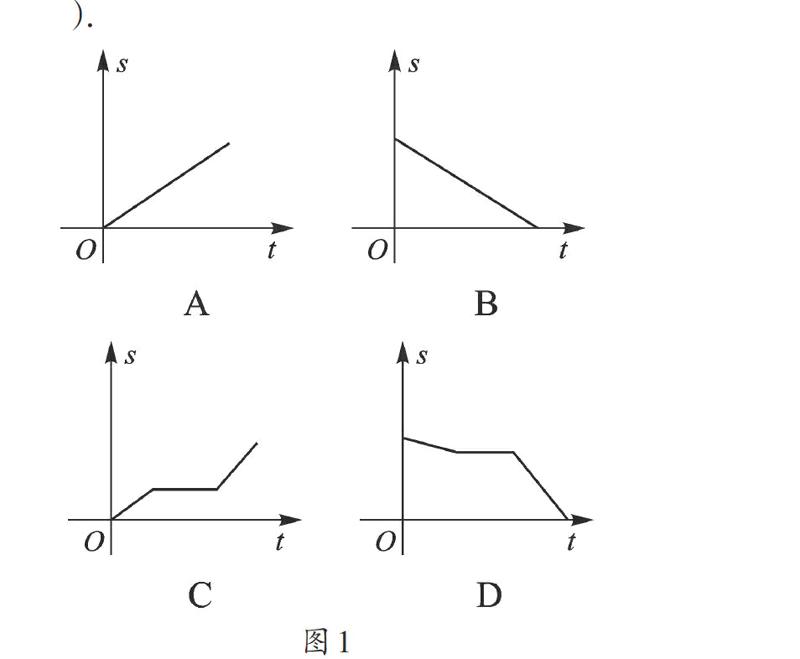
【解析】S是小明離家后到學校剩下的路程,即t=0時,S最大,到達學校時S=0,途中修車時間在變,而S不變,所以選D.
【點評】解答與日常生活相關的問題,要充分利用生活經驗來幫助思考.
考點4 一次函數的圖像及其性質
例4 (2016·廣西玉林)關于直線l:y=kx+k(k≠0),下列說法不正確的是( ).
A.點(0,k)在l上
B.l經過定點(-1,0)
C.當k>0時,y隨x的增大而增大
D.l經過第一、二、三象限
【解析】直接根據一次函數的圖像與性質選擇不正確的選項即可.當x=0時y=k,即點(0,k)在l上,故選項A正確;當x=-1時y=-k+k=0,故選項B正確;當k>0時y隨x的增大而增大,故選項C正確;不能確定l經過第一、二、三象限,此選項錯誤.故選D.
【點評】本題主要考查了一次函數的性質,解題的關鍵是掌握一次函數的性質.
考點5 一次函數的應用
例5 (2016·吉林)甲、乙兩人利用不同的交通工具,沿同一路線從A地出發前往B地,甲出發1h后,乙才出發.y甲、y乙與x之間的函數圖像如圖2所示.
(1)甲的速度是 km/h;
(2)當1≤x≤5時,求y乙關于x的函數解析式;
(3)當乙與A地相距240km時,甲與A地相距 km.
【解析】(1)根據圖像得:360÷6=60(km/h);
(2)當1≤x≤5時,設y乙=kx+b,把(1,0)與(5,360)代入可解得k=90,b=-90,則y乙=90x-90;
(3)令y乙=240,得到x=[113],則甲與A地相距60×[113]=220(km).
【點評】本例(1)也可通過方程求解.(2)為(3)的求解做了鋪墊,(3)是(2)的特殊情形,即求函數值是240時自變量的值.
考點6 反比例函數的圖像及其性質
例5 (2016·黑龍江大慶)已知A(x1,y1)、B(x2,y2)、C(x3,y3)是反比例函數y=[2x]上的三點,若x1 A.x1·x2<0 B.x1·x3<0 C.x2·x3<0 D.x1+x2<0 【解析】∵反比例函數y=[2x]中,2>0,∴在每一象限內,y隨x的增大而減小,∵x1 【點評】本題考查反比例函數圖像上點的坐標特征,解題的關鍵是熟知反比例函數的增減性.本題是反比例函數性質的逆用,有一定的難度. 考點7 反比例函數的應用 例7 (2016·浙江湖州)湖州市菱湖鎮某養魚專業戶準備挖一個面積為2000平方米的長方形魚塘. (1)求魚塘的長y(米)關于寬x(米)的函數表達式; (2)由于受場地的限制,魚塘的寬最多只能挖20米,當魚塘的寬是20米時,魚塘的長為多少米? 【解析】(1)由長方形面積為2000平方米,得到xy=2000,即y=[2000x]; (2)當x=20(米)時,y=100(米),則當魚塘的寬是20米時,魚塘的長為100米. 【點評】反比例函數應用題一般難度不大,解題中要規范解題過程,不因容易而失分. 考點8 一次函數與反比例函數綜合題 例8 (2016·四川廣安)如圖3,一次函數y1=kx+b(k≠0)和反比例函數y2=[mx](m≠0)的圖像交于點A(-1,6)、B(a,-2). (1)求一次函數與反比例函數的解析式; 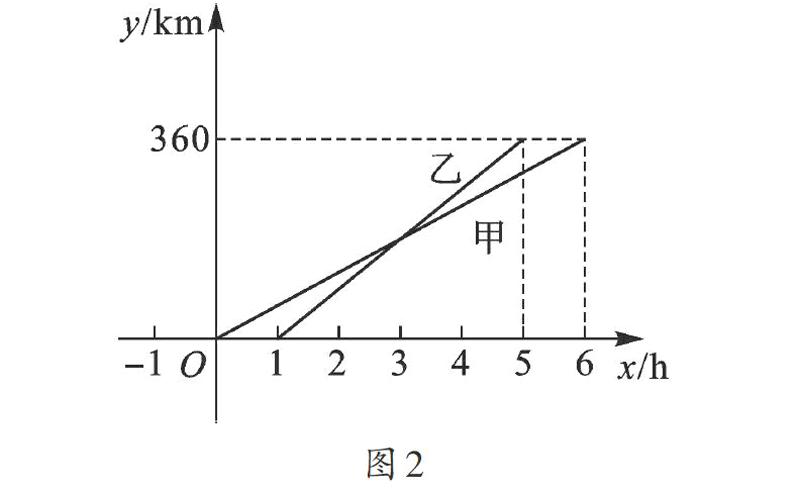
(2)根據圖像直接寫出y1>y2時x的取值范圍.
【解析】(1)將A(-1,6)代入y2=[mx],得m=
-6.∴y2=[-6x].將B(a,-2)代入y2=[-6x],得a=3.∴B(3,-2).將A(-1,6)、B(3,-2)代入y1=kx+b,得[-k+b=6,3k+b=-2.]∴[k=-2,b=4.]∴y1=-2x+4.
(2)由圖3可知,x<-1或0 【點評】求反比例函數解析式需要確定圖像上一個點的坐標,求一次函數的解析式需要確定直線上兩個點的坐標. 考點9 二次函數的圖像及其性質 例9 (2016·廣東廣州)對于二次函數y=[-14]x2+x-4,下列說法正確的是( ). A.當x>0時,y隨x的增大而增大 B.當x=2時,y有最大值-3 C.圖像的頂點坐標為(-2,-7) D.圖像與x軸有兩個交點 【解析】將二次函數解析式配方得y=[-14] ·(x-2)2-3,其頂點坐標為(2,-3),選項C錯誤;∵a<0,∴拋物線開口向下,頂點為最高點,當x=2時,y有最大值-3,選項B正確;由拋物線開口向下,對稱軸為x=2可知,當x>2時,y隨x的增大而減小,選項A錯誤;一元二次方程[-14]x2+x-4=0中,Δ=-3<0,∴這個拋物線與x軸沒有交點,選項D錯誤.故選B. 【點評】本題考查了二次函數的性質,根據拋物線解析式做出圖像,答案便一目了然了. 考點10 二次函數、方程、不等式的應用題 例10 (2016·湖北襄陽)為滿足市場需求,某超市在五月初五“端午節”來臨前夕,購進一種品牌粽子,每盒進價是40元,超市規定每盒售價不得少于45元.根據以往銷售經驗發現:當售價定為每盒45元時,每天可賣出700盒,每盒售價每提高1元,每天要少賣出20盒. (1)試求出每天的銷售量y(盒)與每盒售價x(元)之間的函數關系式; (2)當每盒售價定為多少元時,每天銷售的利潤P(元)最大?最大利潤是多少? (3)為穩定物價,有關管理部門限定:這種粽子的每盒售價不得高于58元.如果超市想要每天獲得不低于6000元的利潤,那么超市每天至少銷售粽子多少盒? 【解析】(1)y=700-20(x-45)=-20x+1600,(x≥45); (2)P=(x-40)(-20x+1600)=-20x2+2400x -64000=-20(x-60)2+8000.∵x≥45,a=-20<0,∴當x=60時,P有最大值,最大值為8000元.即當每盒售價定為60元時,每天銷售的利潤最大,最大利潤為8000元; (3)由題意,得-20(x-60)2+8000=6000,解這個方程得x1=50,x2=70.∵拋物線P=-20(x-60)2+8000的開口向下,∴當50≤x≤70時,每天銷售粽子的利潤不低于6000元.又∵x≤58,∴50≤x≤58.∵在y=-20x+1600中,k=-20<0,∴y隨x的增大而減小,∴x=58時,y有最小值。最小值y=-20×58+1600=440.即超市每天至少銷售粽子440盒. 【點評】用好數量關系“利潤=售價-進價”和“每天銷售的利潤=每盒的利潤×每天的銷量”是建立函數解析式的關鍵. 考點11 函數綜合題 例11 (2016·山東泰安)如圖4,在平面直角坐標系中,拋物線y=ax2+bx+c的頂點坐標為(2,9),與y軸交于點A(0,5),與x軸交于點E、B. (1)求二次函數y=ax2+bx+c的表達式; (2)過點A作AC平行于x軸,交拋物線于點C,點P為拋物線上的一點(點P在AC上方),作PD平行于y軸交AB于點D,問當點P在何位置時,四邊形APCD的面積最大?并求出最大面積; (3)若點M在拋物線上,點N在其對稱軸上,使得以A、E、N、M為頂點的四邊形是平行四邊形,且AE為其一邊,求點M、N的坐標. 【解析】(1)設拋物線y=a(x-2)2+9,把A(0,5)代入得a=-1,∴y=-(x-2)2+9; (2)當y=0時,-(x-2)2+9=0,解得x1=-1,x2=5,∴E(-1,0),B(5,0),設直線AB的表達式為y=mx+n,把A(0,5),B(5,0)代入,得m=-1,n=5,∴y=-x+5.設P(x,-x2+4x+5),則D(x,-x+5),PD=-x2+4x+5+x-5=-x2+5x.∵AC平行于x軸,∴yA=yC=5,∴-x2+4x+5=5,得xC=4,∴AC=4,∴S四邊形APCD=2(-x2+5x)=-2x2+10x,∵-2<0,∴當x=2.5時,四邊形APCD的面積最大,最大面積為12.5; (3)過M作MH垂直于對稱軸,垂足為H,∵MN∥AE,∴△HMN≌△OEA,∴HM=OE=1,NH=OA=5,∴M點的橫坐標為x=1或3;當x=1時,M的縱坐標為8;當x=3時,M的縱坐標為8;N的縱坐標為3或13.∴M點的坐標為(1,8)時,N的坐標為(2,13)或M點的坐標為(3,8)時,N的坐標為(2,3). 【點評】二次函數的綜合題涉及的知識點一般較多,有拋物線與坐標軸的交點坐標求法,幾何圖形的面積,三角形全等、相似,圓等,綜合性較強,有一定難度.在解決有關平行四邊形頂點問題時,通常應用平行四邊形對邊平行且相等,用平移法可找到相鄰頂點間的聯系.解題中常用到數形結合、分類及方程等思想方法. (作者單位:江蘇省興化市戴澤初級中學) 

