淺談如何利用數形結合的方法拓展高中數學解題思路

徐 真

(山東省青島第十五中學 266000)

一、什么是數形結合

數和形是數學學習中兩個最基本的元素，是數學這一學科學習解題的基礎，是攀登數學這座高山的第一階梯.所有的數學問題都是圍繞著數與形這兩方面展開的.每一個幾何圖形都蘊含著大量的數字信息、數量關系；而數量又常常可以通過圖形的方式生動形象的來表達.所以在解決數學問題過程中，常常根據數學問題里數字與答案之間某種聯系，對題目進行針對性的圖形分析，比如應用函數的圖象來直觀地說明函數的性質，這種方式統稱“以形助數”；而有關于圖形的問題也通常借助數字之間的關系進行思考，如應用曲線的方程來精確地闡明曲線的幾何性質，統稱“以數輔形”.數與形之間關系復雜相輔相成，在解析數學難題時，我們往往通過數形結合的方法把數學問題中的數量關系和空間形式相結合，通過數與形的相互解析，從而得出結論.

二、高中數學學習中存在解題思路單一的現象

數學題型千變萬化，形式多樣，教師在教學中不能僅僅將課本上的常規解法教授給學生，特別是當學生面對新題型，無從下手的時候，解題思路單一的問題就會暴露出來.傳統的教學模式下，教師容易照本宣科，開展解題思路教學缺少學生自主參與，容易讓學生坐享其成.通常學生容易將老師上課演示的解題思路變成既定程序，錯誤的意識到只要根據公式進行數字計算，完全不需要思考就可以將同一種類型的題目解出來.但是只要稍微將題目里的數字關系進行變化，學生便又沒了解題模板，解不出題目.失去了自主參與，單一不靈活的解題思維，限定了學生解題方向.事實證明只有一種解題思路是行不通的，必須要有思維的變通性，將原有的解題模板打破，運用更靈活的解題方法，獨立思考運用細致的觀察力和強大的聯想，對題目有一個自身的想法，才能以不變應萬變，將難題迎刃而解.

三、學習方法有問題導致解題思路固定不變通

由于我國的教育模式導致的人才培養機械化，教學模式一成不變化，學生沒有自主學習的意識與能力.縱觀近幾年的高考數學的試題，可以看出試題加強了對知識點靈活應用的考察，以及對公式巧妙轉換能力的探析.這就對學生思維能力的要求加強.怎樣才能提升思維能力？很多考生選擇依靠題海戰術，寄希望于多做題來應對變化多端的考試題，然而僅僅憑借題海戰術的集中式訓練，依舊難以獲得適合自己的科學的思維方式，以至于收效甚微，成績依舊沒法提高.其中最主要的原因是解題思路格式化、固有化造成的，并不是學生自身“不夠用功”的原因，并且就算做再多的題思維依舊被捆綁，學生很難跳出原來的思維定式.我們不要求學生掌握高深的理論，但要求學生形成一定的獨特的審題思維.要學生學會如何從題目所給的條件中去尋求知識點做題，而不是利用題海戰術的“知識點經驗”做題，如何讓學生破繭成蝶，有所改觀？這里就不得不提到數形結合解題法的教學.我國著名數學家華羅庚曾說過:“數形結合百般好，隔裂分家萬事休.”利用好數形結合法可以讓學在重重阻礙中脫穎而出.

四、利用數形結合法解題幫助學生擴展解題思路

數形結合法在高中數學中應用廣泛，與問題式教學法和逆向思維解題法一樣可以幫助學生拓展解題思路，然而不同的是數形結合解題法既可以幫助學生拓展解題思路又可以解決多種數學問題，例如：集合問題，在集合運算中可以采用畫數軸的方法來處理交集、并集、補集的運算，使問題簡單化，解題思路明了.解決三角函數的問題，利用圖象將有關三角函數的單調區間，三角函數大小值的比較等問題圖象化，借助三角函數圖象直觀地處理問題.解決絕對值的問題，利用數軸與絕對值的性質(一點到0點的距離)得到答案，等等.下面我們來重點談談利用數形結合的方法來解決函數單調性的問題.

利用數形結合解決函數單調性問題.函數單調性是函數的一個重要的性質，是高考的熱點考點之一，在解決相關問題時我們要先確定函數單調性和函數的單調區間，數形結合是確定函數單調性的最佳方法，函數的單調區間形象直觀地反映在圖象上.

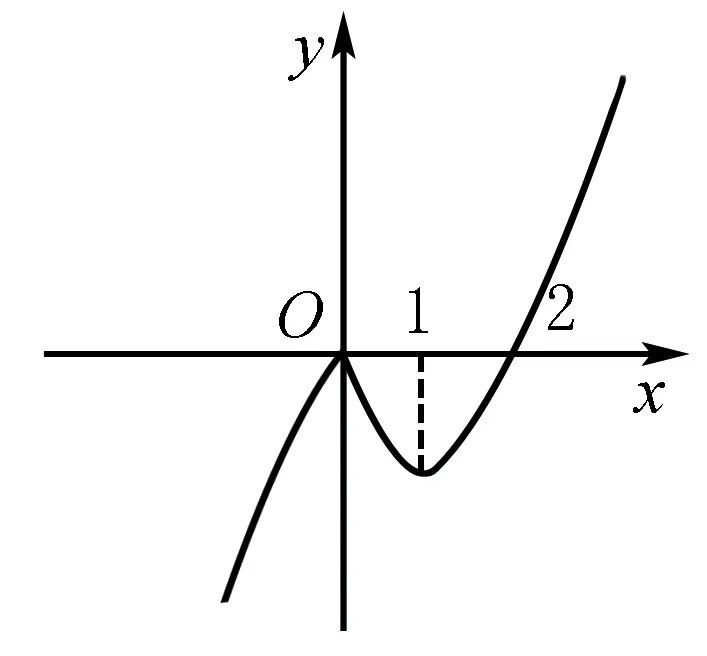
例確定函數y=x|x|-2|x|的單調區間

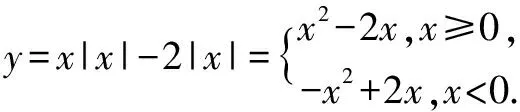
畫出草圖由函數圖象得知函數的單調區間為：

增區間(-∞,0],[1,+ ∞);減區間為[0,1].

通過數形結合的方法解決類似題目，學生不僅可以通過計算得到答案，還能夠在圖形上直觀地看到答案，加以驗證檢查.放棄原有的僅僅利用數字間的關系解題，打破思維的界限以及固有的傳統的解題思路，真正做到了利用多種角度看問題，采用圖形圖象的方式解題.

在新課改下，如何有效地提高學生的主體意識是教育工作者最重視的話題，當學校真正落實學生主體地位，感到自己是數學課堂的主人，才能達到促進學生自主發展的目的，同時這也是素質教育的核心思想.讓學生在課堂學習中有著明確的主體意識，通過多角度思考問題，運用多種解題思路分析問題.強烈的主體意識能激發學生的學習興趣，獨立思考探索新知，學會舉一反三，在老師教學的基礎上能用到多種解題方法和思路.

綜上所述，利用數形結合的方法解析高中數學例題，能有效地拓展學生的解題思路，還能激發學生學習的積極性以及主動性，培養學生的發散思維.所以，高中數學教學中，教師有必要幫助學生利用好數形結合法的解題優勢，幫助學生通過變換性思維去解決實際問題.

[1]李啟龍.第三篇:數形結合思想在函數問題中的應用[J].廣東教育(高中版),2015(2).

[2]梁軍虎.例析數形結合在高考函數中的應用[J].現代教學研究,2012(2).