RANSAC算法求解單應矩陣的具體研究

王博楊

摘要： 本文主要研究RANSAC算法在單應矩陣求解中的應用。具體方法是在單應矩陣的求解過程中，利用RANSAC算法原理，通過不斷地取點、閾值判斷等迭代過程，逐步更新內點集，優化單應矩陣的計算結果，得到更精確解。

Abstract： In this paper， we mainly study the application of RANSAC algorithm in solving single homogeneous matrix. By using the RANSAC algorithm， the interior point set is updated step by step through the iterative process of taking points and thresholds， and the result is optimized to obtain more accurate solutions.

關鍵詞： RANSAC算法；迭代；單應矩陣

Key words： RANSAC algorithm；iteration；homography matrix

中圖分類號：TP317.4 文獻標識碼：A 文章編號：1006-4311（2017）02-0216-02

0 引言

圖像拼接技術能夠將多目視頻圖像拼接成同一平面下的合成圖像，通過該方法的應用可以將無畸變全景監控變為現實，在軍事、交通、科研等領域具有深遠意義。圖像拼接技術的關鍵一步就是多目視頻圖像間的單應矩陣的求解。雖然通過4對不共線坐標就可以求出單應矩陣，但是因為噪聲的存在，在實際取點過程中，一定會存在誤差，導致單應矩陣計算不夠準確，會給后續的圖像拼接造成嚴重影響。

RANSAC算法（Random Sample Consensus）是一種獲得非確定樣本數據的方法，于1981年由Fischler和Bolles最先提出。對于RANSAC算法有一個基本的假設：樣本中包含正確數據（inliers，符合模型的數據）和異常數據（Outliers，不符合模型的數據），通過不斷地更新內點集，找出最優的樣本模型。

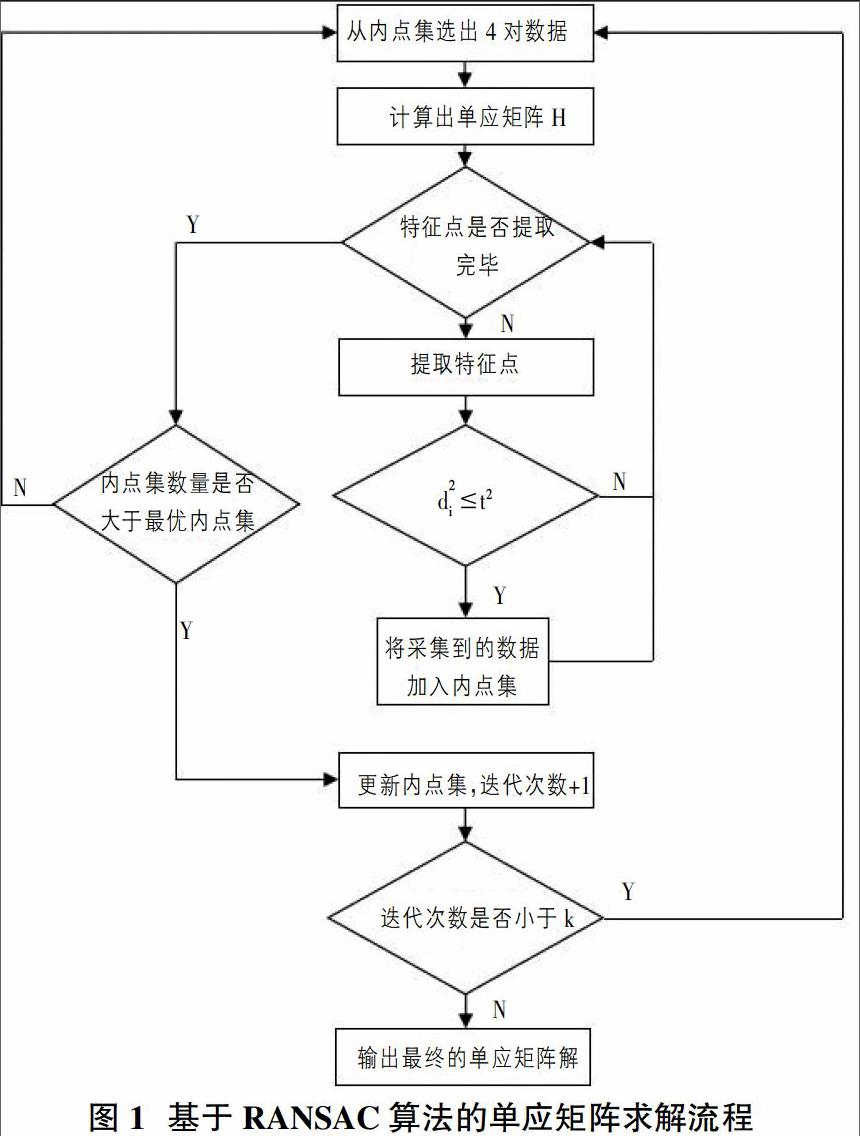
1 基于RANSAC算法的單應矩陣求解流程

為求得單應矩陣的精確值，我們可以通過以下步驟進行：

第一步，先從數據集S中隨機選擇4對樣本。

第二步，根據上述單應矩陣的求解方法，我們可以求得單應矩陣H的初始解，并記為模型M。

第三步，通過模型M計算i點的投影誤差，并通過閾值比較，若d?t，則將i點加入內點集I。

第四步，若通過模型M確定的內點集所包含點的數量大于最優內點集，則更新最優內點集，同時迭代次數，否則從最優內點集中選擇4對樣本重復第二步。

第五步，若迭代次數大于k則結束，最后求得的單應矩陣H是最優解，否則重復第二步。

算法的具體流程如圖1。

2 計算參數的確定

2.1 迭代次數k

根據公式k=確定迭代次數，其中w=內點數/數據總數，p為置信度，我們取值為0.99。

2.2 閾值t

閾值的計算可以通過公式t2=F（α）σ2求得，顯而易見當d?t2時點（x，y）為內點，當d>t2時點（x，y）為外點。A是特征點為內點的先驗概率，為了提高精度，我們取值為0.9。因為是2個自由度，所以n取值為2，通過查表，我們可得F（0.9）=4.605，σ可以通過樣本特征點的提取，采用樣本標準差公式σ=求出，則閾值t就可以通過計算獲得。

3 算法的優化

RANSAC算法因為需要進行的大量的迭代計算和數據處理，因此在某些復雜場景拼接過程中，效率會比較低下?，F在學術界一些優化算法，如2004年由中國科學院的趙向陽、杜利民等人提出的一種全自動穩健的圖像融合拼接算法，該方法通過RANSAC算法迭代計算出最大內點集合后，利用LM（Levenberg-Marquardt）算法對單應矩陣進行優化估計，但是在實際運算過程中并沒有提高多少精度，反而計算效率進一步降低；2012年寧德師范學院計算機系的張世良對算法進行優化，在采集數據樣本的時候通過用K-means聚類算法把N對角點進行分組，每次4對數據求單應矩陣1對數據進行檢驗，不符合要求的數據組直接剔除，運用這種方式減少迭代次數，實際上剔除數據組的計算量并沒有實質性的減少，所以整體算法的效率沒有提高。但是上述兩種方法為我們提高的優化思路有兩點：

一是若是圖像采集質量較低偽匹配點較多的情況下，在選取子集S時可以根據樣本特性等采用特定的選取方案，使用有約束的隨機選取來代替原來的完全隨機選取。

攝像機在同一平面水平排開，攝像機在水平和垂直方向沒有旋轉，那么匹配點間一定有x=xi+λdi+Δxi及y=y+Δyi的約束關系，其中λ為比例系數。通過約束關系很容易把偽匹配點排除掉，極大地減少出錯概率和迭代次數。

二是若是圖像采集質量較高偽匹配點較少的情況下在合理的基礎上簡化運算步驟，上述運算過程中，我們采集每對點坐標都進行了閾值檢測，完全可以采用多點同時檢測的方法：

圖像質量越高，m取值越大，同時檢測的點就越多，算法效率越高。通過實驗，使用上述RANSAC算法，可以快速排除噪聲干擾，準確地求出單應矩陣。

4 結束語

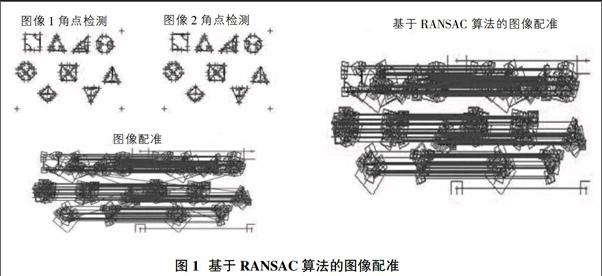
如圖1所示，左側圖像顯示的是沒有使用RANSAC算法的圖像特征點匹配，可以看出出現個別錯誤匹配，這將可能導致后續圖像拼接出現嚴重錯誤。右側圖像是采用了RANSAC算法優化的特征點匹配，完全排除了錯誤干擾，符合運用需求。

參考文獻：

[1]陳藝蝦.改進的ransac算法在圖像配準中的應用[J].計算機科學與探索，2010.

[2]黃梅.基于改進ransac算法的圖像拼接技術[J].海南大學學報，2011.

[3]WeiJei Huang， An Improved RANSAC Algorithm of Color Image Stitching， 2013.

[4]Xiaowei Li， Computing Homography with RANSAC Algorithm：A Novel Method of Registration， 2004.

[5]曲天偉.改進的ransac算法在圖像配準中的應用[J].計算機應用，2010.

[6]AditiMajumder， Rick Stevens. Perceptual Photometric Seamlessness inProjection-Based Tiled Displays， ACM Transactions on Graphics， Vol. 24， No.1 January 2005.

[7]賈瑩.基于Harris角點檢測算法的圖像拼接技術研究[D].吉林大學，2010.

[8]曾琦.Image registration method based on improved Harris corner detector， 2010.

[9]Mark Hereld， Ivan R. Judson， and Rick Stevens. A Measurement Engine for Aligning Multi-Projector Display Systems， Argonne National Laboratory preprint ANL/MCSP958-0502， 2002.

[10]A Way Based On Within-class Scatter Matrix to Improve RANSAC Algorithm， 2012.

[11]Liang Sun.An Improved Harris Corner Detection Algorithm For Low Contrast Image， 2014.

[12]黃梅.面向全景拼接的ransac算法改進[D].海南大學，2011.

[13]陳利軍.圖像角點檢測和匹配算法的研究[J].通信與信息系統，2005.