船舶工業與經濟系統融合程度分析—以青島市為例

徐小峰, 劉家國，郝俊

(1.中國石油大學(華東) 經濟管理學院，山東 青島 266580; 2.大連海事大學 交通運輸管理學院，遼寧 大連 116026)

船舶工業與經濟系統融合程度分析—以青島市為例

徐小峰1, 劉家國2，郝俊1

(1.中國石油大學(華東) 經濟管理學院，山東 青島 266580; 2.大連海事大學 交通運輸管理學院，遼寧 大連 116026)

世界航運市場需求低迷和我國造船產能嚴重過剩，促使全國及各地區船舶工業加快產業結構轉型升級。為保障調整措施的針對性和有效性，首先需要對區域船舶工業與經濟系統之間的互動關系和融合程度進行研究。為此，本文結合青島市1990-2014年經濟數據信息，利用VAR構建了船舶工業與經濟系統變量之間的動態傳遞模型，并運用Granger因果檢驗和Cholesky正交脈沖響應，分析了變量間的關聯效應和影響趨勢。分析結果顯示：青島市船舶工業與經濟系統形成了緊密的互動關系；融資渠道和服務模式對船舶工業發展具有重要影響；產業鏈條和產品種類需要優化配置。

船舶工業；結構調整；VAR模型；區域經濟；產業融合

船舶工業是為海洋運輸、海洋開發和國防裝備等提供載體支持的基礎產業，是集勞動、資本、技術等密集型生產要素于一體的總裝制造業[1-2]。面對世界經濟復蘇遲緩、國內經濟增速放慢、海運市場持續低迷等不利局面，2014年我國船舶工業經受了新船需求不足、產能結構化過剩、海洋工程市場風險突顯等困難考驗，造船完工、新接訂單和手持訂單等三大指標均保持了世界第一的領先位置，造船大國地位進一步鞏固[3]。但是在經濟運行過程中，也暴露出我國船舶工業目前還存在發展后勁不足、企業盈利困難、產能利用率低等問題。為此，政府出臺了若干確保船舶工業與區域經濟協調發展的政策，以加快產業結構轉型升級步伐。那么，船舶工業作為國民經濟發展支柱產業，隨著區域經濟階段變化和產業結構適應調整，與其影響因素將呈現何種關聯關系和變化特征，應如何采取措施促使其產業結構有序優化，成為當前船舶工業結構調整所關注的熱點問題。

關于區域船舶工業與經濟系統的影響研究多是運用關聯效應[4]、投入產出[5]、灰色系統[6]等方法，結合某一時點或區間的投入產出數據，分析其對經濟發展的推動作用和對相關產業的帶動影響。在此基礎上，有研究結合產業升級定位[7]、技術發展趨勢[8]、市場競爭需求[9]等客觀因素，提出了船舶工業產業結構優化調整的模式及對策。綜合上述分析，可看出當前針對船舶工業與區域經濟及關聯產業的動態融合性、互動性研究較為缺乏，而產業關聯效應變化趨勢是反映產業經濟聯系內在規律的關鍵依據，其演化軌跡對產業結構轉型升級政策制定具有重要參考價值。因此，本文以青島市1990-2014年統計數據為基礎，研究船舶工業與區域經濟互動關系及關聯產業的融合程度，考察在不同經濟發展階段船舶工業產業關聯效應的動態變化特征與趨勢，并以此為依據提出青島市船舶工業結構優化方向。

1 研究設計

1.1 研究區域

青島市是國家級船舶產業示范基地和船舶出口基地，船舶工業是推動其藍色經濟發展的支柱產業之一，現已形成涵蓋船舶、海工裝備、游艇、配套零部件、集裝箱生產于一體的船舶海工產業鏈。目前青島市已規劃建設完成的基地有黃島區海西灣和即墨女島兩大基地，正在規劃建設以船舶海工為主的膠南董家口基地，錯位發展的產業格局基本形成(如圖1)。

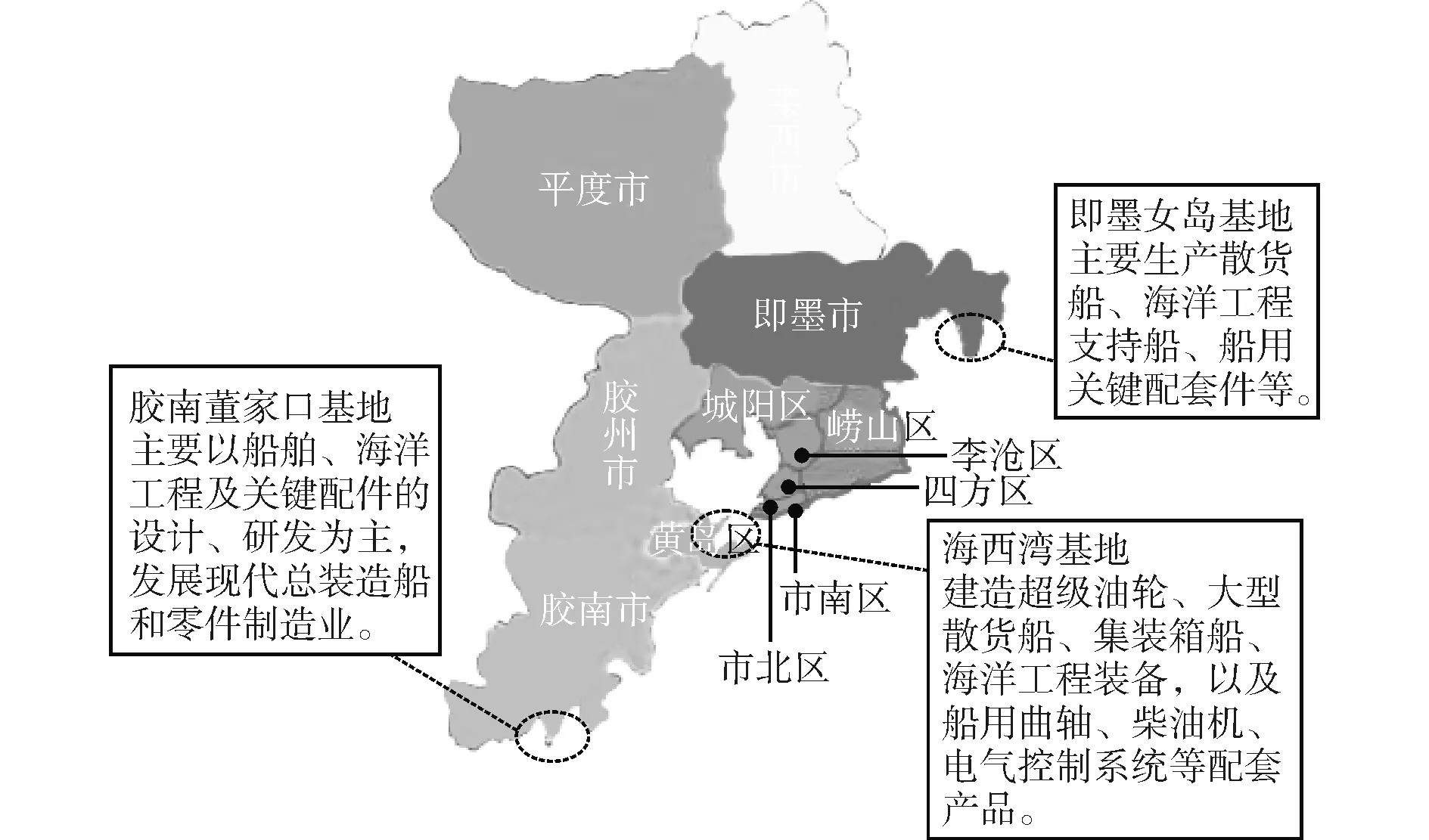
圖1 青島市船舶工業產業格局Fig.1 The shipbuilding industrial pattern of Qingdao city

雖然青島市船舶工業已形成了以特色龍頭企業為支撐的產業聚集區，但是由于良好的地理優勢和前期旺盛的市場需求，該行業內還存有大批以小型船舶修造為主、經營規模偏小、產品附加值低的船舶制造及配套企業，隨著市場需求持續低迷和競爭日趨激烈，產能結構化過剩問題逐漸顯現，影響了青島市區域經濟的整體發展水平。遏制產能進一步過剩，促進產業結構優化升級，實現船舶工業與區域經濟協調發展，將為青島市實現藍色經濟騰飛提供重要契機。本文以青島市1990-2014年的經濟運行狀況為基礎，分析區域船舶工業與經濟系統之間的互動關系及融合程度，為產業結構轉型升級提供決策依據。

1.2 研究方法

1.2.1 運用VAR模型選取影響變量

以經濟理論為基礎的結構化分析模型需預先確定問題及解釋變量，并由此推斷變量間的關聯關系[10]，而區域船舶工業與經濟系統之間的作用影響屬于非結構化問題，難以通過理論分析直接確定解釋變量。因此，選用向量自回歸模型(vector autoregression models, VAR)來描述經濟變量間的非結構化動態關聯。這是由于VAR是基于數據的統計性質構建模型，不存在問題識別和內生變量解釋等復雜過程，能夠高效處理多變量相關分析、預測和隨機擾動對系統動態沖擊等問題[11]。

假設區域船舶工業與經濟系統變量之間的VAR(p)模型數學表達式是

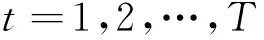
(1)

式中：Yt是代表區域船舶工業發展的k階內生變量向量;Xt是區域經濟系統中影響船舶工業的m階外生變量向量;Ai和D分別是k×k和k×m階的系數估計矩陣;p是滯后階數；N是樣本總數。需要預先確定的是：經濟變量X和Y的候選范圍、向量滯后階數p(保證隨機擾動項服從向量白噪聲)，在模型求解過程中，為避免出現“偽回歸”現象，還需對時間序列向量進行平穩性檢驗。

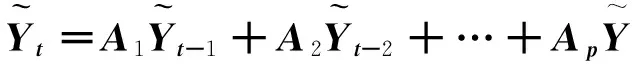
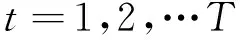
(2)

若引入滯后算子L，則又可以表示為

(3)

其中，A(L)=Ik-A1L-A2L2-L-APLP為滯后算子多項式。通過估計An(n=1,2…p)系數矩陣取值，可以確定區域經濟系統中與船舶工業關聯較為緊密的經濟變量。

1.2.2 采用Granger檢驗確定互動關系

上述構建的動態模型可解析區域船舶工業與經濟系統變量之間的關聯關系，但無法識別其中的因果互動關系，而Granger檢驗可從統計意義上分析變量間的因果性[12]，這對區域船舶工業結構優化具有重要的決策參考價值。

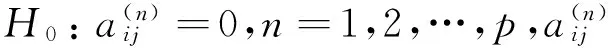
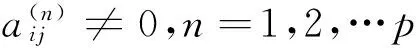
(4)

如果S1小于F的臨界值，則接受原假設：yjt能Granger引起yit；否則拒絕原假設。其中，RSSi是yit方程uit的殘差平方和，RSSi是不yit滯后變量的方程殘差平方和。由于F檢驗要求滿足高斯分布，所以也可用一般的漸進等價檢驗來代替

(5)

如果S2小于的χ2臨界值，則接受原假設；否則拒絕原假設。

1.2.3 利用IRF方法衡量融合程度

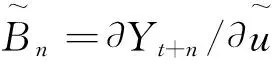
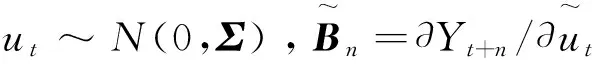
(6)

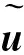
(7)

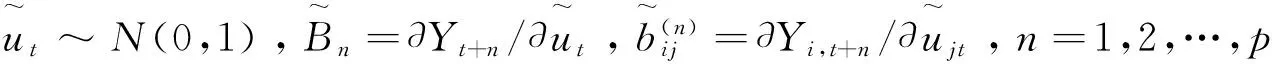
由此可以看出，Cholesky正交分解法中脈沖響應結果取決于VAR(p)模型中的變量次序。

2 變量描述與數據處理

2.1 變量描述

本文著重研究分析區域船舶工業與經濟系統中變量的互動關系與融合程度，并選取青島市典型區域作為研究樣本，從中國船舶工業年鑒和青島市統計年鑒提取了VAR(p)模型中10個初始內生變量的數據信息，數據跨度從1990～2014年共25個觀測值。VAR(p)模型中初始內生變量的信息描述及數據處理如表1所示。

表1中1～3變量代表區域經濟系統的發展狀況，其中，sv與船舶工業發展密切相關，是衡量區域船舶工業發展水平的關鍵變量。4～6個變量代表區域貿易、客運、旅游等與船舶工業相關市場的價值產出。7、8變量表示社會經濟和金融服務等與船舶工業相關渠道的資金投入，尤其在國際航運和海工市場低迷情況下，創新金融模式、擴大融資渠道已成為船舶企業降本增效的關注重點。9、10變量表示區域城市化程度和經濟吸納能力，反映了與船舶工業發展環境相關的基礎條件。

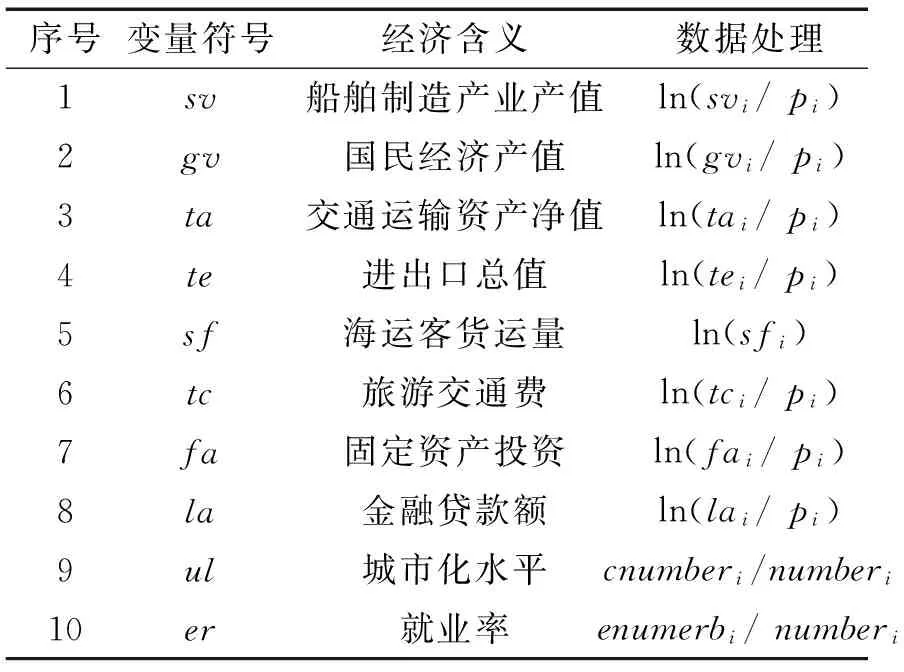
表1 變量說明

注：1. 假定價格因素長期線性穩定，pi表示第i年的價格影響指數，i=1,2, …,n；2.cnumberi、enumberi、numberi表示第i年末區域非農業人口數、就業人口數、總人口數。

2.2 數據處理

為消除價格因素和數據異方差影響，以1990年為基期對部分變量的原始數據進行了標準化和對數取值。同時，為避免VAR模型出現“偽回歸”現象，還需對模型中內生變量數據進行平穩性檢驗，以保障OLS參數估計的一致性。選用單位根檢驗中的ADF方法進行變量數據檢驗，平穩性檢驗結果如表2所示。

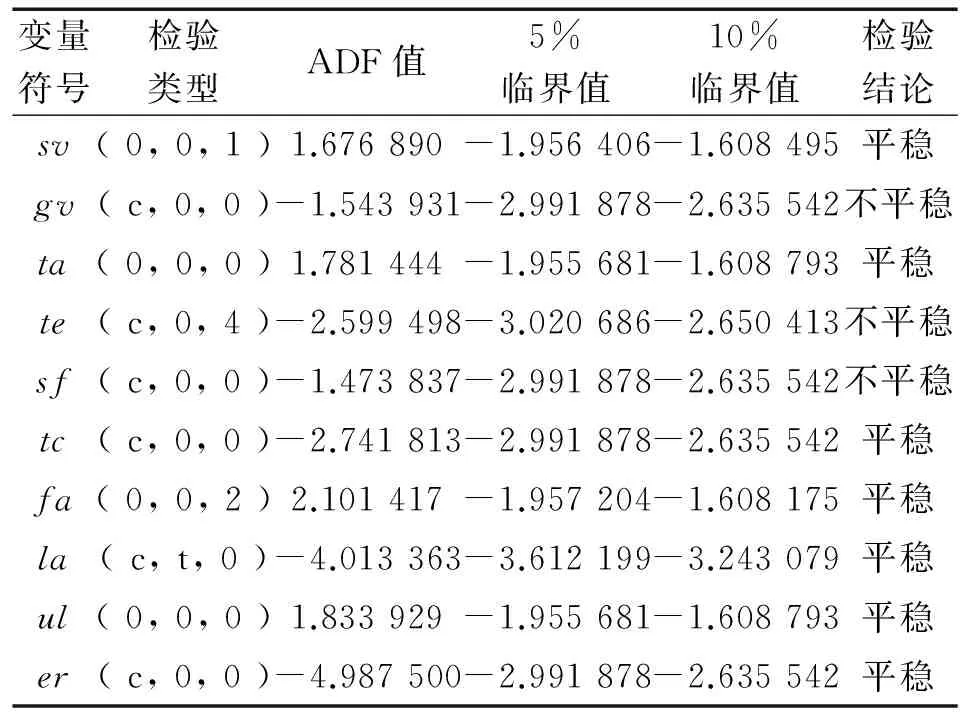
表2 ADF平穩性檢驗結果

注：er變量是在1%顯著水平下趨于平穩。

由表2可以看出，內生變量中gv、te、sf未通過平穩性檢驗。為保障VAR模型參數的一致性，對未實現平穩的變量取一階差分后再進行ADF單位根檢驗，結果表明上述變量在1%顯著水平下均實現了平穩。另外，構建VAR(p)模型中還需解決滯后階數p的選擇問題。在進行ADF檢驗時一般可獲得滯后階數，這種定階方法是以消除時間序列相關性為目的，存在定階過高、影響模型自由度等弊端。在VAR(p)模型構建過程中，既要考慮模型動態特征完整反映，還要兼顧參數估計數量，為此，采取LR、FPE、AIC等傾向較低定階的信息準則方法確定模型滯后階數為2。

3 實證分析與結果討論

3.1VAR模型構建分析

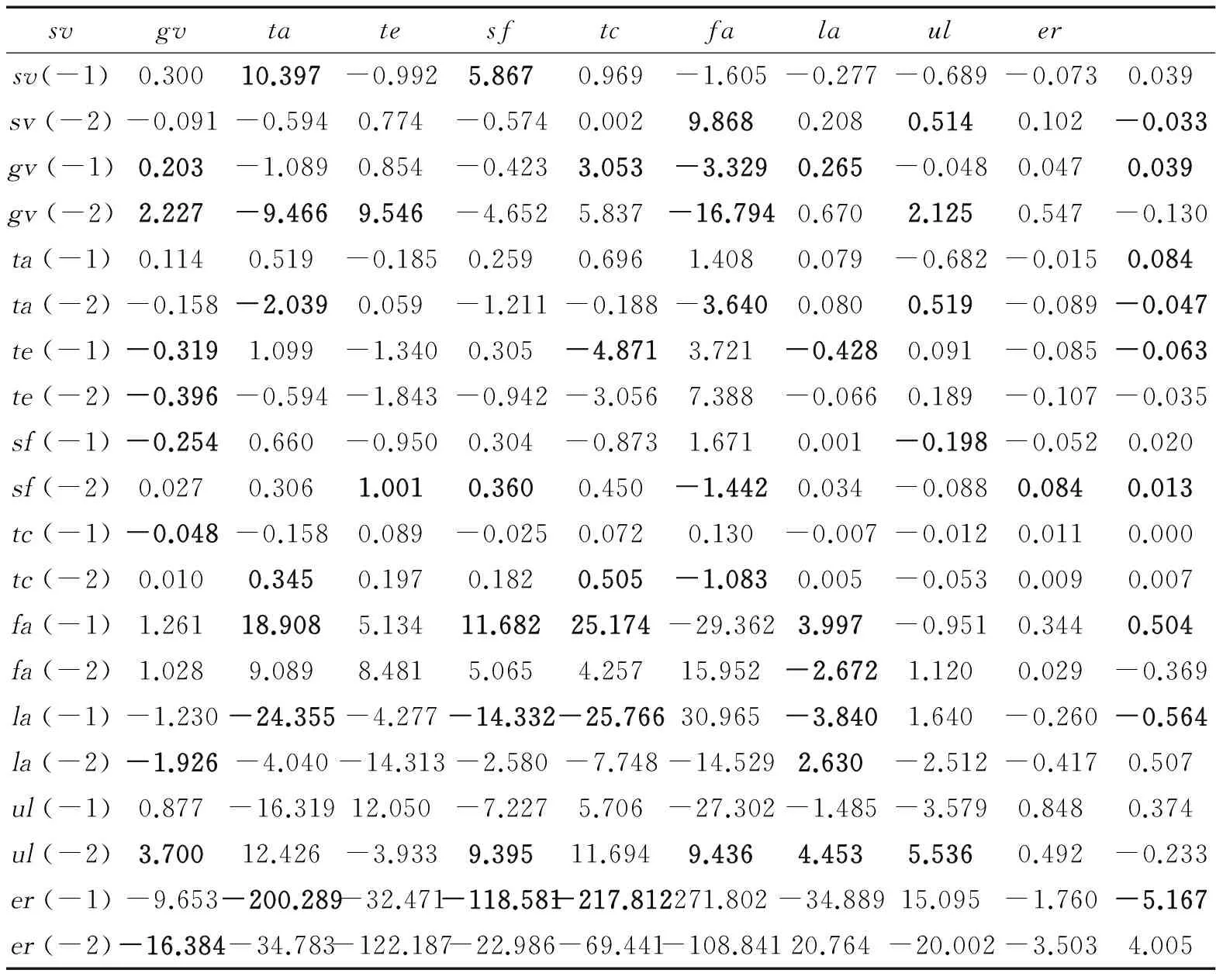
為有效分析區域船舶工業與經濟系統之間的動態關系，文中以青島市為例，構建了10維的VAR模型，并采取多種信息準則確定了滯后階數，建立的VAR(2)模型系數估計如表3所示。估計結果顯示多數系數的t統計量在10%顯著水平下并不顯著，究其原因可能是同一方程中變量的滯后值產生了多重共線性，但這不影響模型滯后階數選擇。

VAR(2)模型整體的擬合優度為0.970 673，表明擬合效果較好。同時，為保障模型脈沖響應分析的有效性，還需對模型進行穩定性檢驗。文中采取

AR根檢驗方法，估計的VAR(2)模型所有根模倒數都在單位圓內(如圖2)，表明模型是穩定的。這說明盡管青島市船舶工業與經濟系統之間存在著復雜的關聯影響，但由sv、gv、ta等10個變量構成的系統是穩定的。

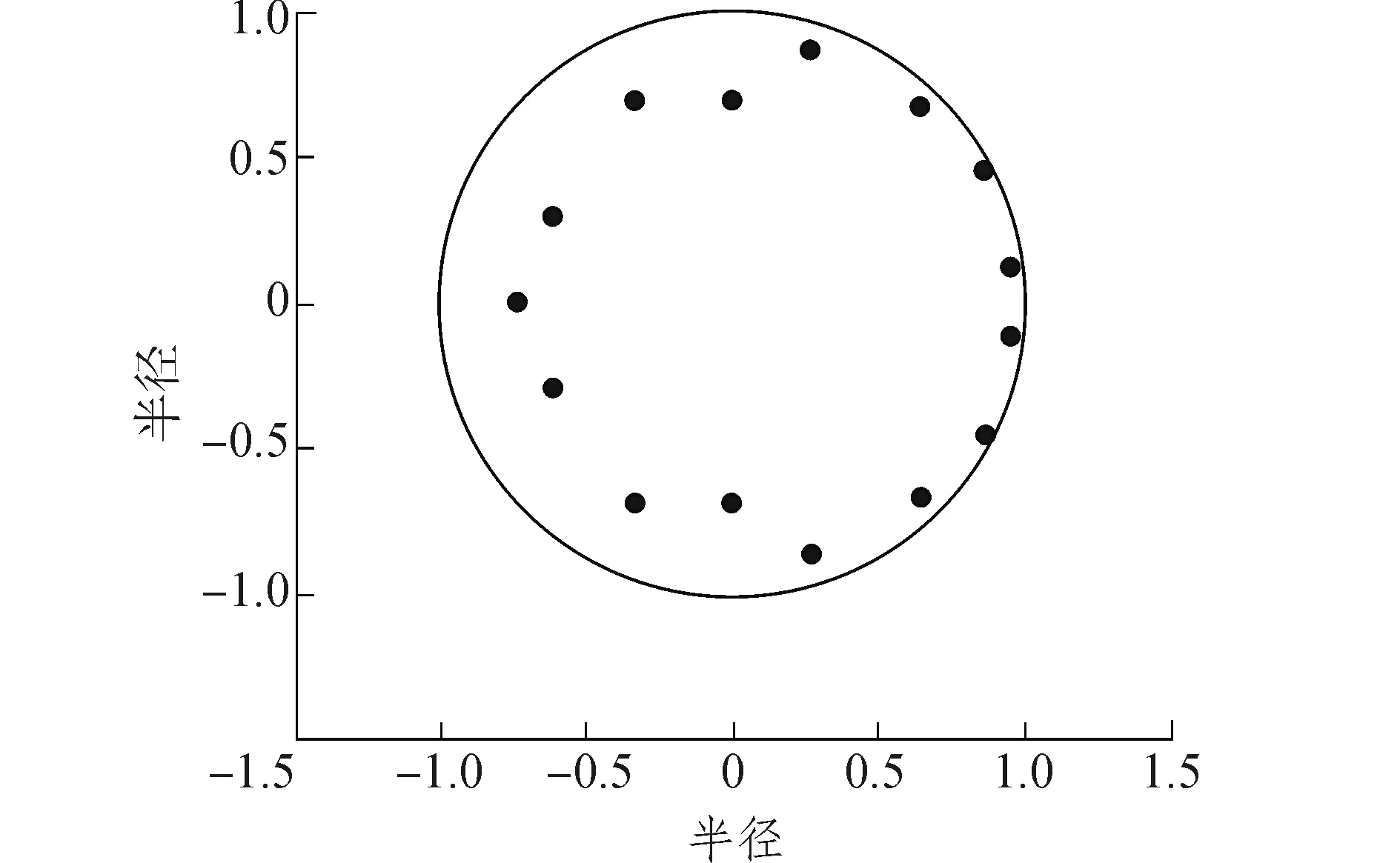
圖2 VAR(2)模型穩定性檢驗Fig.2 VAR(2) model stability test

svgvtatesftcfalaulersv(-1)0.30010.397-0.9925.8670.969-1.605-0.277-0.689-0.0730.039sv(-2)-0.091-0.5940.774-0.5740.0029.8680.2080.5140.102-0.033gv(-1)0.203-1.0890.854-0.4233.053-3.3290.265-0.0480.0470.039gv(-2)2.227-9.4669.546-4.6525.837-16.7940.6702.1250.547-0.130ta(-1)0.1140.519-0.1850.2590.6961.4080.079-0.682-0.0150.084ta(-2)-0.158-2.0390.059-1.211-0.188-3.6400.0800.519-0.089-0.047te(-1)-0.3191.099-1.3400.305-4.8713.721-0.4280.091-0.085-0.063te(-2)-0.396-0.594-1.843-0.942-3.0567.388-0.0660.189-0.107-0.035sf(-1)-0.2540.660-0.9500.304-0.8731.6710.001-0.198-0.0520.020sf(-2)0.0270.3061.0010.3600.450-1.4420.034-0.0880.0840.013tc(-1)-0.048-0.1580.089-0.0250.0720.130-0.007-0.0120.0110.000tc(-2)0.0100.3450.1970.1820.505-1.0830.005-0.0530.0090.007fa(-1)1.26118.9085.13411.68225.174-29.3623.997-0.9510.3440.504fa(-2)1.0289.0898.4815.0654.25715.952-2.6721.1200.029-0.369la(-1)-1.230-24.355-4.277-14.332-25.76630.965-3.8401.640-0.260-0.564la(-2)-1.926-4.040-14.313-2.580-7.748-14.5292.630-2.512-0.4170.507ul(-1)0.877-16.31912.050-7.2275.706-27.302-1.485-3.5790.8480.374ul(-2)3.70012.426-3.9339.39511.6949.4364.4535.5360.492-0.233er(-1)-9.653-200.289-32.471-118.581-217.812271.802-34.88915.095-1.760-5.167er(-2)-16.384-34.783-122.187-22.986-69.441-108.84120.764-20.002-3.5034.005

注：加粗系數表示t統計量在10%顯著水平下顯著。

在表3中估計的系數雖然大多不顯著，但是從部分顯著的系數中也可以發現青島市船舶工業與經濟系統之間的關聯影響：

sv-gv——船舶工業與青島市經濟發展存在顯著關系。船舶工業將會帶動機械、鋼鐵、化工、儀器儀表等相關產業協同發展，這是推動青島市經濟發展的重要動力之一。同時，青島市工業發展水平和基礎設施配套能力又會對船舶工業形成支撐或制約作用，隨著滯后階數增加，這種作用效果會不斷增強。

sv-te——船舶工業與青島市進出口貿易存在顯著關系。船舶產品附加值高，其出口將有效帶動青島市貿易發展，但是由于船舶產品制造周期較長，見效較慢，在滯后1階和2階中，對進出口貿易發展呈現了一定的負面影響。

sv-tc——船舶工業與青島市旅游業存在顯著關系。作為濱海旅游城市，旺盛的游艇、客輪需求將有效帶動船舶工業發展。考慮到船舶產品投資周期長且占用資金多，在滯后1階對旅游業將會產生負面影響，從滯后2階后則表現出積極促進作用。

sv-la——船舶工業與青島市金融服務業存在顯著關系。在船舶建造過程中，由于船東議價能力較強，船企往往需要進行項目墊資，這將占用企業過多的流動資金。為保持正常的生產經營，船企多需向地方金融機構進行融資，隨著建造進度推移和技術難度增加，這種需求將會變得更加強烈。

sv-er——船舶工業與青島市就業水平存在顯著關系。船舶工業作為多要素密集型產業，隨著技術改進和生產模式變革，對從業人員的素質和能力要求越來越高，因而，從就業角度看，隨著柔性制造和數字化造船的推廣，行業擠出的負面效應將會變得更加明顯。

無論VAR(2)模型的系數估計是否顯著，在“新常態”經濟形勢下，文中對青島市船舶工業與經濟系統變量之間的影響符號判斷基本符合預期經濟意義。作為青島市的六大支柱產業，船舶工業發展對區域工業、進出口貿易和旅游業具有重要影響。作為總裝制造業，青島市船舶工業對產業鏈的完整性和經濟系統的匹配性提出了較高要求，不僅需要大規模的固定資產投資，還要求有通暢的融資渠道與環境。同時，隨著造船技術與生產模式的變革，船舶工業對城市基礎環境和從業人員素質也有了更高要求。

表4 Granger因果關系檢驗結果

注：表示在10%顯著水平下，存在Granger因果關系。

3.2 變量互動關系分析

依據上述VAR(2)模型中系數估計的顯著狀況，可分析得出區域船舶工業與經濟系統變量之間的部分關系，但此種分析結果具有一定的主觀局限性，變量之間究竟存在何種互動(單向或雙向)關系，還需要統計意義上的檢驗分析。為此，對VAR(2)模型中的變量進行Granger因果關系檢驗，結果如表4所示。

從表4結果可看出：一方面， gv、te、sf、tc、fa、la、ul、er等單變量及其滯后項對sv具有聯合顯著性，即這些單變量均是sv的Granger原因，包含ta在內的所有變量及其滯后項對sv具有聯合顯著性，即經濟系統中所有變量共同是sv的Granger原因，這說明青島市船舶工業內生性良好，與區域經濟系統形成了緊密的發展關系。另一方面，sv是gv、ta、te、tc、la等變量的Granger原因，與gv、te、tc、la等變量存在雙向互動關系，這說明青島市船舶工業與區域工業體系、進出口貿易、旅游交通和金融服務等已形成了有效的溢出與反饋機制。sv與ta、sf、fa、ul、er等變量存在單向影響關系，表現出了較強的外生性。這其中，青島市交通運輸主要以陸路為主，對船舶工業產生的行業帶動作用不強；船企產品主要以散貨船、集裝箱船和海工平臺為主，未對海運客貨市場形成有力支撐；船舶工業發展投資周期長、見效緩慢，很難對固定資產投資產生顯著影響。同時，船舶工業發展對城市化程度、就業吸納能力也未產生明顯的影響作用。

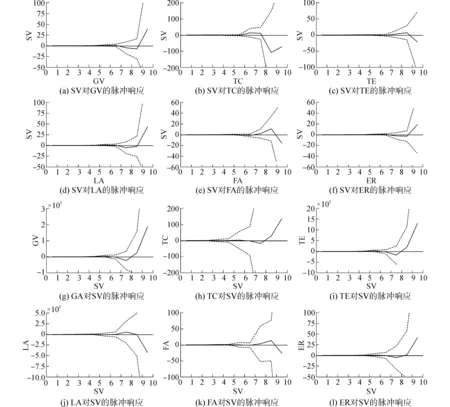
圖3 VAR(2)模型部分變量的脈沖響應函數Fig.3 Impluse response function of VAR(2) model variables

3.3 產業融合程度分析

文中估計出的VAR(2)動態傳遞模型系數很難得到精確解釋，而Granger因果檢驗得到的互動關系也僅是對關聯效應的統計確認。為明確模型中變量間的影響程度，分析青島市船舶工業的產業融合狀況，還需借助VAR模型的脈沖響應函數。由于Cholesky正交脈沖對模型變量次序極度敏感，所在在做脈沖響應之前，需要對模型變量進行排序，根據變量之間的外生影響確定排序如下：

在構建的VAR(2)模型中共含有10個變量，會產生100個脈沖響應函數。在這里只選取對一個正標準差信息沖擊反應較強的脈沖響應函數(如圖3)

由變量的脈沖響應函數可以看出，船舶工業無論是作為脈沖變量還是響應變量其作用發揮都有較長的時滯，這與船舶工業投資周期長、見效慢的特點是相吻合的。

從圖3中可看出，在當期給sv一個正向沖擊后，在長達7期內gv呈現下行波動趨勢，從第8期開始出現上升拐點，sv對gv的帶動作用明顯增強，并形成持續的正向響應。這表明船舶工業作為投資規模巨大的基礎產業，在中短期內對青島市經濟將會產生較明顯的“抽血效應”，但從長期角度看，其對區域經濟將產生明顯的拉動作用。sv對la的脈沖響應函數表面上與gv類似，但影響關系卻大不相同。一定時期內船舶工業的良性發展會使船企資金充裕，因而向金融機構貸款的意愿不強烈，但隨著造船進度推進和技術復雜程度的提高，企業對資金的需求將會明顯增強。同樣，sv對er的脈沖響應函數也呈現中短期負相關，長期正相關的趨勢，表明船舶工業發展雖然對從業人員素質和能力提出了更高要求，但從長期看對就業還會產生正向帶動作用。

在當期給定正向沖擊后，sv對te的脈沖響應函數從第7期開始上升，到第9期出現明顯下降。這表明船舶工業對青島市進出口貿易影響較大，在船舶產品建造期間，配套設備、零部件等進口都將帶動貿易增長，但隨著產品交付使用，這種影響將在

短期內消失。同樣，sv對fa也存在類似的影響，在船舶工業發展初期需要大量的基礎設施投入，這將有效帶動固定資產投資增加，一旦設施建成投入使用，對固定資產投資的影響也會逐漸降低。但sv對tc的影響則與其他不同，接受沖擊后tc先呈現上升趨勢，在第8期后出現明顯下降，并從第9期開始反彈。這表明青島市船舶工業在中短期將會對旅游業發展產生支撐作用，但在大型客輪、游艇等產品上的短板，在長期將會顯現出負面影響。

給gv、tc、te、ta、er、ul等變量一個正向沖擊后，在第7或8期后都會對船舶工業發展產生明顯的推動作用。這表明青島市船舶工業與區域經濟高度融合，在產業結構中占有重要地位。la與sv呈現先正向后負向的波動趨勢，說明船舶建造融資貸款在中短期有利于青島市船舶工業發展，但在長期將會將會削弱船企的資金流動能力，給企業乃至整個行業帶來負面影響。同樣，加大固定資產投資中短期能夠拉動青島市船舶工業發展，但是單純依靠這種外延式推動難以形成核心競爭力，長期看不利于船舶工業的健康發展。

4 結論

作為“海上絲綢之路”國家戰略實施的重要支撐產業，船舶工業發展將會對區域經濟系統產生深遠影響。本文結合青島市實例，借助VAR方法構建了區域船舶工業與經濟系統變量之間的動態傳遞模型，并運用Granger因果檢驗和脈沖響應函數對變量間的互動關系、融合程度進行了確認檢驗和量化分析。分析結果顯示：

1)青島市船舶工業與經濟發展已形成了良好的溢出與反饋互動關系，與進出口貿易、旅游、金融服務等行業的融合程度較高；

2)船舶建造產生的資金需求給船企帶來了較大的經營壓力，船企需要平衡資金流動與融資貸款之間的影響關系；

3)固定資產投資對船舶工業傾斜不足，船舶產品不能完全滿足青島市航運旅游市場需求。

基于上述結論，本文給出青島市船舶工業與區域經濟協調發展的政策建議：

1)考慮船舶工業的發展特點和對區域經濟的深遠影響，其發展規劃應從中長期著手；

2)營造良好的金融服務環境，建立風險投資和融資保障機制，拓寬融資渠道、創新金融模式以幫助船企緩解資金壓力；

3)積極打造并升級船舶工業產業鏈條，確立明顯的產業定位與淘汰機制。

[1]XU J J, YIP T L. Ship investment at a standstill? An analysis of shipbuilding activities and policies[J]. Applied economics letters, 2012, 19(3): 269-275. [2]徐小峰, 趙金樓. 網絡效應下我國船舶工業參與國際競合的提升路徑分析[J]. 經濟問題探索, 2012(2): 54-59.

[3]中國船舶工業行業協會. 2014年船舶工業行業發展情況報告[N]. 中國船舶報, 2015-01-23. China Shipbuilding Industry Association. Shipbuilding industry development report in 2014[N]. China Ship News, 2015-01-23.

[4]吳錦元. 船舶工業對國民經濟的作用與貢獻[J]. 船舶工業技術經濟信息, 2001(1): 8-1.

[5]呂靖, 張麗麗, 梁晶. 船舶制造業蕭條對關聯產業的間接經濟影響[J]. 商業研究, 2013(8): 25-28.

[6]張光明, 支園園, 周惠, 等. 江蘇船舶產業結構分析[J]. 造船技術, 2012(5): 6-9, 19. ZHANG Guangming, ZHI Yuanyuan, ZHOU Hui, et al. The analysis of shipping industry structure of Jiangsu[J]. Marine technology, 2012(5): 6-9, 19.

[7]應長春. 長三角地區船舶產業發展態勢[J]. 上海造船, 2009(1): 1-7, 14.

[8]季建偉. 世界船舶工業的產業轉移及我國船舶工業支柱產業的選擇[J]. 船舶物資與市場, 2006(2): 23-25.

[9]ZAKARIA N M G, ALI M T, HOSSAIN K A. An overview of Bangladeshi shipbuilding in the light of competitive parameters[J]. Journal of shipping and ocean engineering, 2011, 1: 8-19.

[10]GUJARATI D N. Basic econometrics[M]. New York: McGraw-Hill Higher Education, 2002.

[11]高鐵梅. 計量經濟分析方法與建模[M]. 2版. 北京: 清華大學出版社, 2009.

[12]GRANGER C W J. Developments in the study of co-integrated economic variables[J]. Oxford bulletin of economics and statistics, 1986, 48(3): 213-228.

[13]張幼文, 薛安偉. 要素流動對世界經濟增長的影響機理[J]. 世界經濟研究, 2013(2): 3-8. ZHANG Youwen, XUE Anwei. Factor mobility and its impact on world economic growth[J]. World economy studies, 2013(2): 3-8.

[14]史永東, 田淵博. 異常情況下基于VARX模型的中國投資者行為研究[J]. 中國管理科學, 2014, 22(4): 17-24. SHI Yongdong, TIAN Yuanbo. The behavioral study of Chinese investors based on the VARX under abnormalities[J]. Chinese journal of management science, 2014, 22(4): 17-24.

Integration degree between regional shipbuilding industry and economic system taking Qingdao as an example

XU Xiaofeng1, LIU Jiaguo2, HAO Jun1

(1.College of Economics and Management, China University of Petroleum, Qingdao 266580, China; 2.Transportation Management College, Dalian Maritime University, Dalian 116026, China)

The weak demand for the global shipping market and the serious oversupply of China’s shipbuilding capacity have prompted the national and regional shipbuilding industry to accelerate industry restructuring and upgrading. To ensure the pertinence and effectiveness of related measures, the interaction relationship and degree between the regional shipbuilding industry and the economic system need to be studied first. In this paper, the economic data of Qingdao from 1990-2014 are compiled. A dynamic transfer model between the shipbuilding industry and economic variables is then constructed by utilizing vector autoregression model(VAR). Then, Granger causality test and Cholesky orthogonal impulse response are used to analyze the correlation effects and trend influence of variables. Analysis results show that the shipbuilding industry and the economic system in Qingdao have a close relationship; financing channels and service modes have an important influence on the development of the shipbuilding industry; and the industrial chain and product category need optimized allocation.

shipbuilding industry; structure adjustment; VAR model;regional economics;industrial integration

2015-12-10.

時間：2016-12-12.

國家自然科學基金項目(70673014)；教育部人文社會科學研究項目(15YJC630144)；山東省軟科學項目(2014RKE28017)；山東省高等學校人文社會科學研究項目(J13WG67)；青島市社會科學規劃研究項目(QDSKL130415).

徐小峰(1982-)，男，副教授，博士； 劉家國(1979-)，男，教授，博士生導師.

劉家國，E-mail:lliujiaguo@gmail.com.

10.11990/jheu.201512034

F207

A

1006-7043(2017)01-0140-07

徐小峰, 劉家國，郝俊. 船舶工業與經濟系統融合程度分析—以青島市為例[J]. 哈爾濱工程大學學報， 2017, 38(1): 140-146. XU Xiaofeng, LIU Jiaguo, HAO Jun. Integration degree between regional shipbuilding industry and economic system taking Qingdao as an example[J]. Journal of Harbin Engineering University,2017, 38(1): 140-146.

網絡出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20161212.1631.018.html