基于區間兩階段的城鎮污水處理技術優選模型

王 劍,付正輝,郭懷成(北京大學環境科學與工程學院,北京 100871)

基于區間兩階段的城鎮污水處理技術優選模型

王 劍,付正輝,郭懷成*(北京大學環境科學與工程學院,北京 100871)

為解決現有污水處理技術優選方法的片面性、主觀性和不確定性,本研究以環境、社會和經濟效益最大化為目標,采用區間兩階段隨機規劃的方法,構建模型測算區域新增廢水的最優處理方法和處理量,并應用于滇池盤龍江流域,結果表明在廢水排放量較大的區域,多種污水處理技術的組合要優于選擇任意一種處理技術.其中,厭氧-缺氧-好氧工藝由于運營和投資成本低,在處理規模較大時,具有明顯優勢,而間歇式循環延時曝氣活性污泥法則適用于廢水排放規模較小的城鎮,其污染物去除效果要優于厭氧-缺氧-好氧工藝和氧化溝法.

區間兩階段隨機規劃；不確定性；污水處理技術；優化模型；滇池流域

隨著社會經濟發展水平的提高,人口規模的持續增大,我國廢水排放量也在逐年增長.2014年,全國廢水排放量716.2億t,相比2011年增長57億t.依托“十一五”、“十二五”期間對環保基礎設施的投入,污水處理能力的增速總體快于廢水排放的增速,至2014年底全國城市污水處理率已經達到82.12%[1].但是,由于運營成本偏高和管道建設滯后等原因,使得實際處理能力低于預期值,造成大量處理能力閑置,甚至污水處理廠停工.多數城鎮污水處理廠在選擇處理技術和建造規模時,僅憑經驗或污染物去除率進行決策,缺乏對運營和建造成本等多方面的考慮,使得選擇的處理技術及建造規模并非最優.

目前我國在線運營的城鎮污水處理廠中,二級生化工藝占據了主導地位,其中氧化溝(OD)、傳統活性污泥法(CAS)、間歇式活性污泥法(SBR)、厭氧-好氧工藝(A/O)、厭氧-缺氧-好氧工藝(A2/O)和曝氣生物濾池(BAF)6種工藝是全國 90%以上污水處理廠的主體工藝類型[2].不同技術在污染物去除效果、運營成本和投資成本等方面都存在較大差異,其中運營成本、投資成本還與建造規模相關,因素之間的復雜聯系,使得綜合的評價污水處理技術變得更加困難.實際操作過程中,還需要考慮到技術應用中的諸多不確定性,如環境系統的隨機性和人為操作的不確定性.因此,為解決在選擇污水處理技術時,面臨的片面性、復雜性和不確定性,亟待開展對污水處理技術評價和優選方法的研究.

目前,部分學者采用數理統計的方法,通過搜集的污染源普查數據,構建城鎮污水處理投資和運營費用函數,最終回歸分析得到不同處理規模和排放水平下的污水處理廠費用效益函數[3-5].該方法能求得兩類數據之間的客觀聯系,但是難以對多種數據進行綜合分析,使得結論相對片面.另一部分學者,嘗試用模糊數學和層次分析的方法來對不同處理技術進行綜合評價.他們通過建立涉及投資成本、運營成本、處理效果、管理水平等多層次的指標體系,以費效分析和模糊綜合評價方法對指標進行量化,并按照相應權重加和,求得處理技術的最終得分[6-8].雖然,該方法對污水處理技術進行了全面的評價,但由于定性指標的量化方法和指標間權重的測算過程,存有較大的主觀性,就使得不同研究的評價結果都存在較大差異.

隨著不確定性優化理論研究和計算機技術的發展,污水處理技術的優選被當作隨機規劃問題來求解.Tsai等[9]基于隨機動態規劃方法建立了污水處理廠的決策模型,對各工藝環節的不同技術進行最佳的優選組合,以提升整體的處理性能.林玉鵬等[10]引入區間數變量,構建城市污水廠的優化模型,以解決參數和數據獲取的不確定性.但是,該方法更多應用于技術參數的優化改良[11-12],對污水處理技術優選方面的研究相對較少.

因此,本研究將構建基于區間兩階段的隨機優化模型,在環境、社會和經濟效益最大化的目標下,對污水處理技術進行優選,求得在未來不同廢水排放水平下,3種常見污水處理技術(A2/O),氧化溝法和 SBR的改進工藝(ICEAS)的最優分配量,并以云南滇池盤龍江流域的污水處理廠為例,開展應用研究.

1 模型方法及原理

不確定性優化模型分為隨機優化模型、區間數優化模型和模糊優化模型[13].隨機優化模型是將不確定性用概率的形式來表征,以求得不同風險水平下的最優解,但其概率則需要大量的基礎數據作支撐,使得模型對基礎數據的要求較高.區間數優化模型則是以區間形式來表征模型的參數或數值,一方面有助于消除數據的不確定性,另一方面使得決策者可以通過偏好的優先級來作出更加靈活的決策.模糊優化模型,則是將目標和約束變量的主觀不確定性轉化為模糊關系,再建立隸屬函數,取最大值后求得最優解.考慮到隸屬函數的主觀性,以及本次研究的目的和現有數據的形式,因此,采用隨機和區間數結合的優化方法構建模型.

區間-兩階段隨機優化模型(ITSP)是區間規劃和隨機規劃的結合,具有了兩種不確定性優化方法的優點.一方面它能以區間數的形式去表征不確定性,且數據獲取較為容易;另一方面,它還有兩階段隨機規劃的懲罰、補償機制,使得結果在一定時間上最優.

ITSP模型的基本形式如下:

式中:和{R±}代表區間數形式的模型參數或決策變量.Ph為隨機變量 wl在 h水平下的概率值,且

針對該模型的求解,Huang等[14]首次提出交互式算法將模型轉化為求解上下界目標函數的兩個子函數,即 ,進而通過兩步算法,先求解下界,再將結果代入上界,最終得到穩定的區間解.

2 案例研究

2.1 模型概述

盤龍江是滇池最主要的入湖河流之一,北起于嵩明縣西北梁王山,南至滇池東岸海埂村入湖口,全長105km,多年平均徑流量3.57億m3,流域面積達903km2.盤龍作為一條橫穿昆明市區的河流,對昆明市民的生產、生活起著極其重要的作用.同時,盤龍江是“牛欄江-滇池補水工程”的重要輸水線路,還承擔著改善滇池水環境,并在昆明市發生水危機時,提供城市生活及工業用水的重要責任.因此,保障盤龍江流域的水環境安全顯得尤為重要.

考慮到2015～2025年,未來10年流域人口規模的增長和生產經營活動的需求,預計其廢水排放量將遠超現有的污水處理能力.所以,本研究針對流域現有的3座污水處理(表1)的擴容改造構建了ITSP模型.

表1 研究區域污水處理廠基本概況[15]Table 1 Basic information of sewage treatment plants in research areas

昆明的3座污水處理廠的來水水質差異性小,經過處理后,廢水污染物排放可以達到一級B類的排放標準,除 TP外,處理后均可達到一級 A類標準

[16-17].3種處理方法都能使廢水達標排放的情況下,不同技術的深度處理效果、投資和運營成本方面之間區別,成為了選擇最優技術的主要維度.

模型在假定未來廢水水質不變的情況下,針對新增廢水的排放量,有選擇的對3座處理廠進行擴容,并通過兩個階段的廢水分配,使管理者選出最佳的處理技術.在第一階段廢水分配中,流域管理者需要預先判斷各個污水處理廠計劃處理量,并進行擴容改造.當廢水排放量超出預期時,則需要進行第二階段廢水分配,并產生環境經濟懲罰.懲罰分為兩部分,一部分是由于新增廢水對污水處理廠運營造成的壓力負荷,另一部分是考慮到擴建所需的時間,因此默認新增廢水為不進行處理的直接排放,將對環境造成損傷.

該模型以整個系統的環境、社會和經濟效益最大為目標函數,同時考慮到各技術的污染物去除率、運營成本和投資建設成本等問題.通過控制擴容總量約束、廢水排放量的總量約束、年運營費用和每年投資建設費用的控制等約束條件,來保證系統的長期有效運作.同時,本模型采用區間數對系統的新增污水排放量、各處理廠的污染物處理率、單位運營成本、單位投資成本等不確定性因素進行表征.

2.2 污水處理廠優化配置ITSP模型

2.2.1 目標函數

模型由收益和成本兩部分組成,收益主要以排污收費和廢水處理后產生的水資源價值來表征,成本則由計劃外直接排放造成的環境污染和資源損耗、運營成本、投資建設成本和閑置處理能力的折舊費用,共6部分組成.其中,運營成本分為計劃內和計劃外運營成本,且考慮了設備正常運轉時的維修和折舊等費用.

式中: Wit±是t時期(a),i污水處理廠的計劃處理量,為第一階段決策變量,萬m3/d;Tith±是t時期,i污水處理廠在新增污水排放量為 DEth±時(概率水平為 PI)的計劃外廢水排放,即直接排放量,也為第二階段決策變量,萬m3/d;Hith±是t時期,i污水處理廠的計劃內剩余處理能力,萬m3/d;ΔCitk±為t時期,i污水處理廠單位水量對k污染物的去除量, t/萬m3; NTPVit±為t時期,i污水處理廠在計劃內運營時的總運營成本,萬元;TPVit±為t時期,i污水處理廠的單位水量的運營成本,萬元/萬 m3; PPt±為t時期,污水處理廠由于計劃外廢水的排入,導致運營負荷過載的處罰成本,萬元/萬 m3; TCim±為i污水處理廠,在擴容方案m時的單位投資成本;為t時期,i污水處理廠在h廢水排放水平和擴容方案m時的二元變量,選擇擴容時值取1,否則取0;TEm為擴容方案m的擴容量,萬m3/d; Bk為k污染物(分別是BOD5、NH3-N和TP)的污染當量值,依據排污收費標準,此處數值分別為: 0.5kg、0.8kg和 0.25kg;PR1、PR2為污染物在正常排放和超標排放兩種情況下的污染物當量收費標準;PW為單位水資源的影子價格,此處為2.41元/m3[18];TN為研究時期 t的總時長,此處為 10a;f為閑置的污水處理容量的設備折舊率, 4.53%[19].

2.2.2 約束條件

(1)擴容總量約束

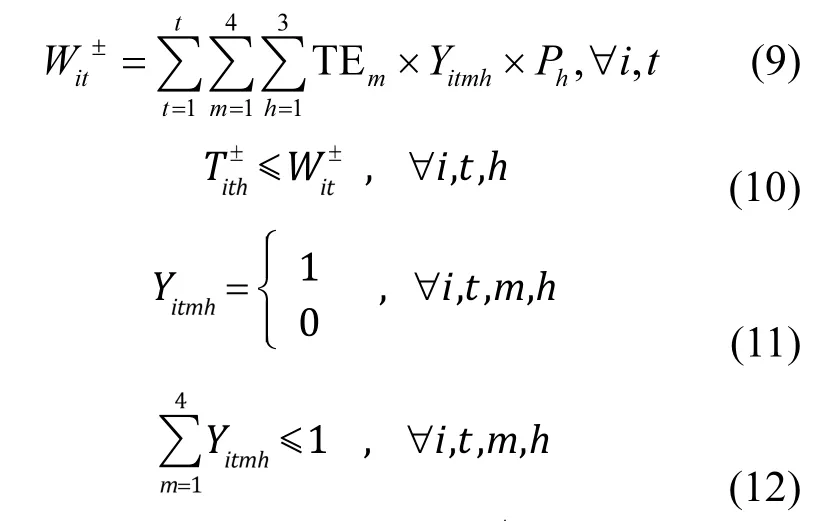
計劃分配的污水排放量Wit±會受到i廠在t時刻以前(包含t)總擴容量的限制.污水處理廠有4種擴容選擇TEm,分別為5、10、20和30,單位為萬m3/d,也可以選擇不擴容,此時為0.

(2)廢水總排放量約束

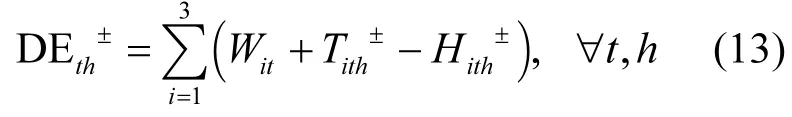
3座污水處理廠需要分攤未來新增的全部廢水排放量 DEth±(表 2),部分為計劃內的實際處理量(Wit±-Hith±),它們將產生環境社會經濟效益;另一部分計劃外廢水排放量,將直接排放到受納水體中,并產生懲罰.

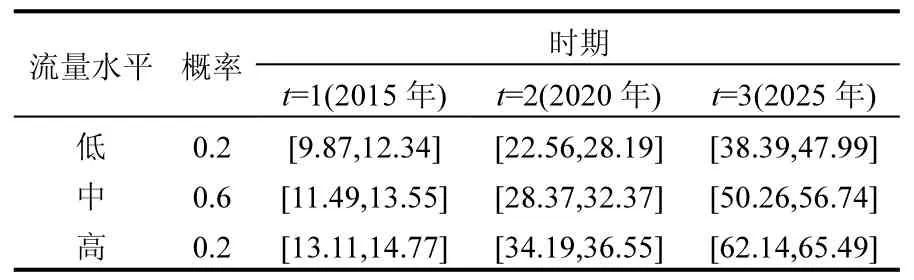
表2 新增廢水排放量(以2013年為基準)/(萬m3/d)Table 2 Increased wastewater discharge(based on 2013)

(3)運營成本的總費用約束

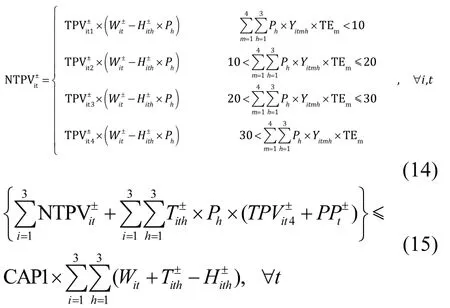
污水處理廠單位水量的運營成本會受到其擴容規模的影響,因此NTPVit±存在4種可能的返回值(式 14).另外,為了保證污水處理廠的正常運作,其每年運營總成本應該低于CAP1(昆明市單位廢水排放的收費標準及政府財政扶持的和[20])乘以廢水排放量的金額,此處CAP1為1.5元/m3.

(4)投資建設成本的總費用約束

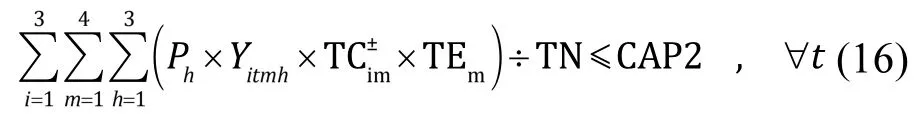
政府管理者每年在污水處理廠上投資建設的費用,應該低于政府上一季度制定的財政預算CAP2.本研究的CAP2數據來自于“滇池流域‘十二五’水污染防治規劃”中,對盤龍江流域污水處理設施的投資預算,折合成年后數值為1384.5億元/a,并假設之后10a的投資與近5a基本持平.同時,結合其他研究成果[23-24]和污水處理廠的實際投資數據,得到各污水處理技術在不同擴容水平下的投資建設成本(表4).

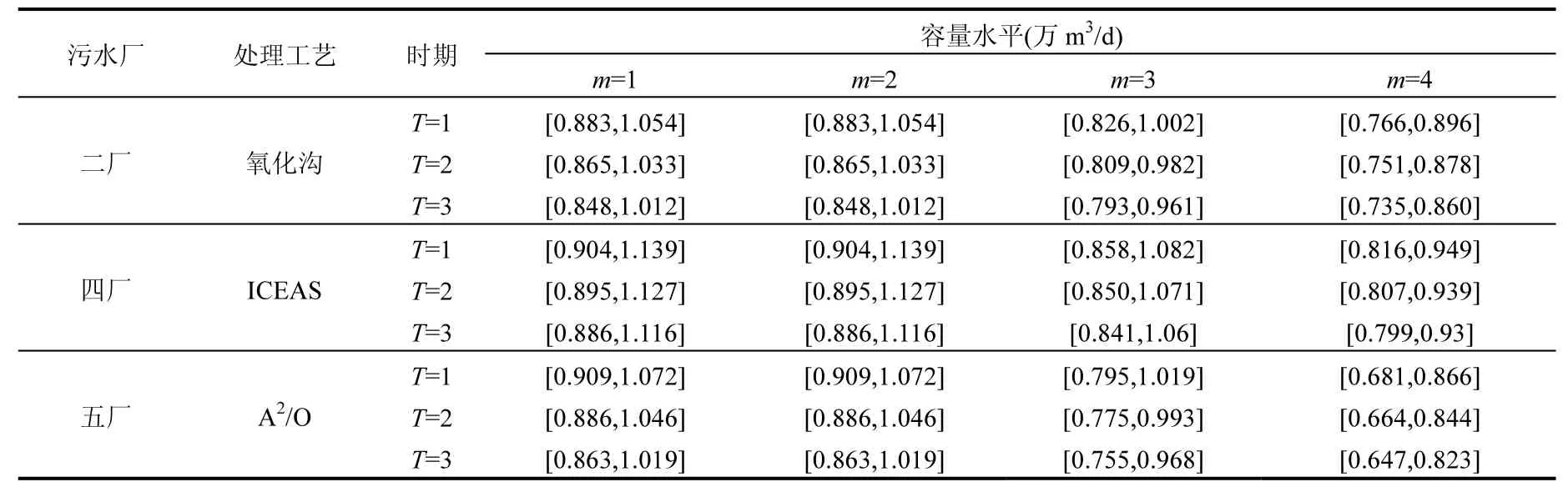
表3 不同處理廠在不同時期和容量水平下的單位運營成本[21-22][(萬元?d)/萬m3]Table 3 Operating cost of sewage treatment plants in different periods and capacities [(×104RMB?d)/104m3]

表4 不同污水廠在不同擴容水平下的單位建設成本[(萬元?d)/萬m3]Table 4 Construction cost of sewage treatment plants in different periods and capacities [(×104RMB?d)/104m3]

根據2007～2009年昆明市污水處理二、四、五廠的實測數據,結合相關研究[25-30],得到不同污水廠在不同時期單位水量污染物的去除率,并假定進水的污染物濃度與 3座污水廠的歷史進水平均濃度保持一致,最終求得污水處理廠在不同時期單位水量的污染物去除量(表5).

表5 不同污水廠單位水量污染物的去除量(t/萬m3)Table 5 Amount of removed pollutants of sewage treatment plants (t/104m3)

3 結果分析

經過模型計算,系統的最優期望收益是[470.43,1165.73]×106元/a,此時污水處理廠擴容建設的潛在期待值在和 fopt+之間變動,分別對應極端保守和樂觀的污水處理策略.

從模型運算的結果,可以得到污水處理技術在3個時期的最優計劃污水處理量(圖1).結果表明在盤龍江流域,A2/O、氧化溝法和ICEAS法均有一定可取之處,3種污水處理技術的組合要優于選擇其中任意一種技術.

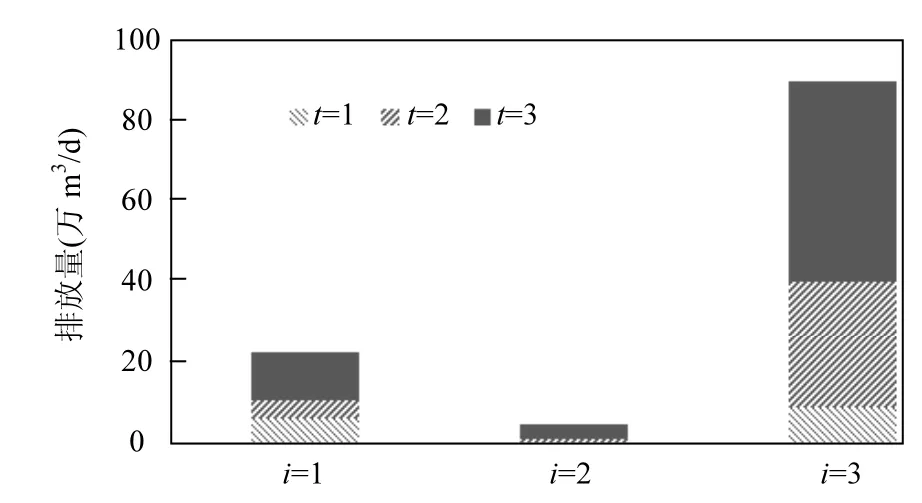
圖1 3座污水處理廠在不同時期的最優計劃處理量WitFig.1 Optimizedpre-regulated allocation of three sewage treatment plants in different periods

相較而言,A2/O法在新增廢水排放量較大的情況下具有比較明顯的優勢,在t=2和t=3時期,采用A2/O法計劃處理的廢水達到總量的84.8%和 75.38%,因為隨著污水處理廠規模的增大,A2/O法的處理成本,相比另外 2種技術會低10%左右,同時,其單位建設成本也遠低于另外 2種技術.

在 3個時期,二廠(氧化溝法)將分別計劃處理6,4.6和12萬m3/d,各年份計劃處理量的差異較小.在不同廢水排放水平下,氧化溝法都具有一定的競爭力,工藝具有較強的穩定性,比較適用于中等規模的污水處理廠.

此外,就目前的技術水平而言,ICEAS法并不適用于昆明這類廢水排放量增長較快的大城市,僅在 t=2,t=3時刻,有 1和 4萬 m3/d的處理量.ICEAS法對污染物的去除效果總體都要優于A2/O法和氧化溝法,但它的處理成本和投資成本在污水處理規模較大時,要遠超另外2種方法,而在處理規模較小時,運營和投資成本均在可接受范圍內,因此它在排放量水平較低的城鎮具有更高的應用價值.

模型可供選擇的擴容量為4類,再結合3種排放水平下的擴容選擇,最終得到多種擴容組合,按照,計算得到污水處理廠在不同時期的最優擴容方案(表6).

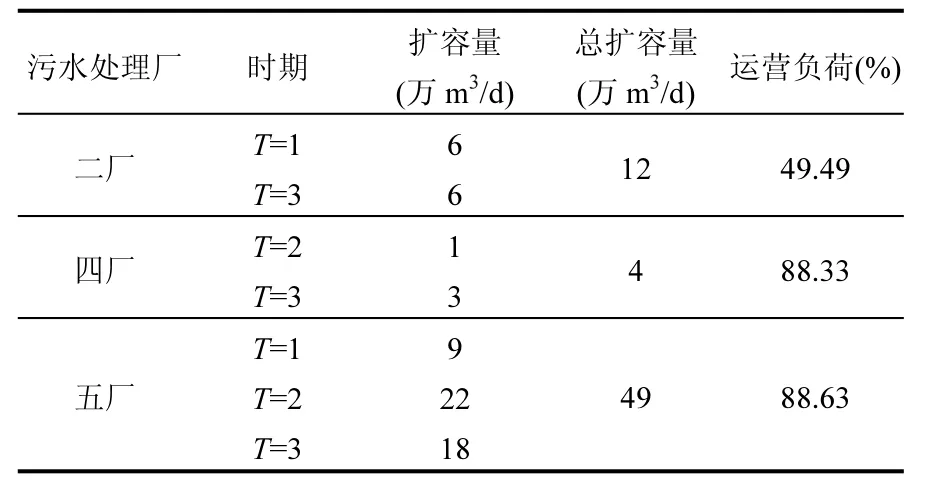
表6 污水處理廠各時期的擴容量及平均運營負荷Table 6 Capacity expansion and operation load of sewage treatment plants in different periods

模型計算結果顯示,第2階段的控制變量計劃外直接排放( )的數值基本為0,僅在t=3,高流量水平的情況下才存在0.489萬m3/d的直接排放污水.在模型計算過程中,將污水處理廠的投資建設成本,分攤至每年,使得每年的總收益中投資建設成本的占比要低于運營成本和環境收益的占比.所以,模型采取了較為積極的擴容策略,即在面臨新增廢水排放時,優先選擇擴容,而非計劃外的直接排放.積極的擴容策略也使得污水處理廠總體的平均運營負荷僅為75.48%,其中3種處理技術的差異明顯,四廠(ICEAS法)和五廠(A2/O法)的運營負荷較高,平均負荷可達到88%以上,在廢水排放水平較高的時期,甚至能達到92%以上.

但是,氧化溝法因為污染物去除效率差于A2/O和 ICEAS法,且在各技術運營成本差距較小的情況下,導致二廠(氧化溝法)容易被其他技術所取代.從污水處理廠的實際處理量(圖2)可以看出,在t=2時,氧化溝法的實際處理量顯著降低,這也是導致其負荷偏低的最直接原因.

總體而言,模型運算結果與我國目前不同處理規模下,各污水處理技術的市場占有情況保持一致[31-32].采用積極的擴容策略對于像滇池等污染較為嚴重,卻具有極高的社會經濟價值的湖泊河流,有較高的現實意義.在監測數據較少,且精度難以確定的區域,本方法有助于解決技術優選中的不確定性,但局限在于污水處理技術方法的運行數據,且對模型構建過程的合理性提出了較高要求.

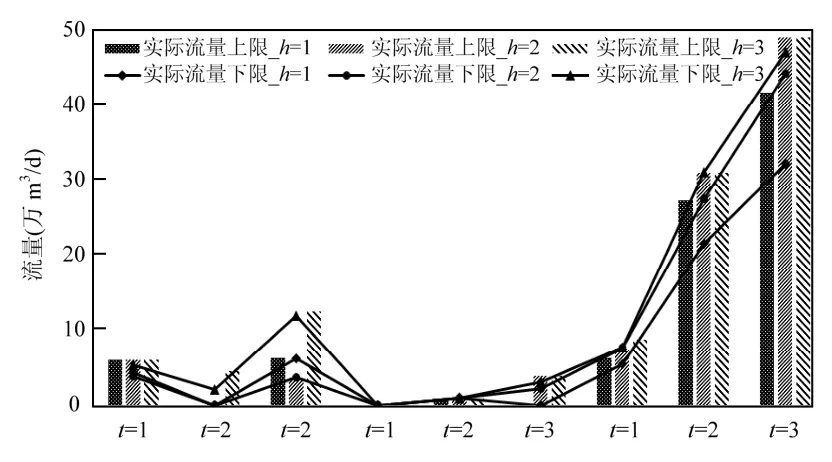
圖2 不同時期和流量水平下污水處理廠的實際處理量Fig.2 Actual capacity of sewage treatment plants in different periods and flow levels

4 結論

4.1 本研究通過構建區間兩階段隨機優化模型,對污水處理技術進行優選,綜合考慮了處理過程產生的環境經濟效益和費用,以及區域的廢水排放、污水處理運營建造成本和污水處理規模等約束條件.通過區間數來表征環境系統的隨機性和數據獲取的不確定性,并以兩階段來設置懲罰、補償機制,求得在時間上的最優解.同時,決策者還可以根據實際情況和對風險的不同偏好,來制定適宜的技術組合方案.

4.2 模型求解后的結果表明,對廢水排放量較大的區域而言,污水處理技術的組合要優于選擇某種單一的處理工藝.其中,A2/O技術在廢水排放量較大的區域具有明顯的優勢,因為其處理和建造成本隨著處理量的增加顯著減低;而ICEAS法則適用于規模較小的污水處理廠.同時,在污水處理規模較小時,污染物的去除效果好的技術更適宜被采用;在污水處理規模較大時,運營和建設成本則成為主導因素.

4.3 模型的懲罰值對計算結果有較大的影響,根據研究區域的實際情況和管理目標,可以對其進行調整.由于本次案例分析的區域為滇池流域,因而采取了較為嚴格的管控措施,導致計算結果偏向保守,污水處理廠的總運營負荷在70%～80%左右,造成一定的資源浪費.另外,也與模型未考慮污水處理廠的抗沖擊負荷能力有關.同時,如何核算污水處理后產生的環境效益,也會對污水處理技術和擴容方案的最優解帶來一定的影響.

[1] 環保部.中國環境狀況公報 [R]. 2014.

[2] 楊 勇,王玉明,王 琪,等.我國城鎮污水處理廠建設及運行現狀分析 [J]. 給水排水, 2011,37(8):35-39.

[3] 於 方,牛坤玉,曹 東,等.基于成本核算的城鎮污水處理收費標準設計研究 [J]. 中國環境科學, 2011,31(9):1578-1584.

[4] 劉 杰,鄭西來,高 超,等.城鎮污水處理廠用地,運行及建設費用研究 [J]. 環境工程學報, 2010,(11):2522-2526.

[5] Chen H W, Chang N B. A comparative analysis of methods to represent uncertainty in estimating the cost of constructing wastewater treatment plants [J]. Journal of Environmental Management, 2002,65(4):383-409.

[6] 李凡修,梅 平,陳 武.多元集對模型在污水處理廠改造決策中應用 [J]. 環境科學與技術, 2004,27(6):92-94.

[7] 郭勁松,楊 淵,方 芳.西部小城鎮污水處理技術評價指標體系研究 [J]. 重慶大學學報:社會科學版, 2005,11(2):14-17.

[8] 王佰偉,曹升樂.工業廢水治理效果多目標評價方法研究 [J].山東大學學報(工學版), 2007,3:016.

[9] Tsai J C C, Chen V C P, Beck M B, et al. Stochastic dynamic programming formulation for a wastewater treatment decisionmaking framework [J]. Annals of Operations Research, 2004, 132(1-4):207-221.

[10] 林玉鵬,曾光明.考慮不確定性因素影響的城市污水處理廠優化設計模型研(I) [J]. 湖南大學學報:自然科學版, 2000,27(4):94-100.

[11] 徐恭賢,韓 雪.非線性污水處理過程的多目標優化 [J]. 化工學報, 2013,64(10):3665-3672.

[12] Rivas A, Irizar I, Ayesa E. Model-based optimization of wastewater treatment plants design [J]. Environmental Modelling & Software, 2008,23(4):435-450.

[13] 鄒 銳,郭懷成,劉 磊.洱海流域環境經濟相協調的農林土地利用不確定性系統規劃 [J]. 環境科學學報, 1999,19(2):186-193.

[14] Huang G H. IPWM: an interval parameter water quality management model [J]. Engineering Optimization, 1996,26(2): 79-103.

[15] 孫迎雪,吳光學,胡洪營,等.昆明市污水處理廠進水水質特征分析 [J]. 環境科學與技術, 2013,36(7):147-152.

[16] 邱令冰.昆明市城市污水處理廠現狀調查和分析 [J]. 云南環境科學, 2006,25(B06):36-38.

[17] 孫迎雪,吳光學,胡洪營,等.基于達標保證率的昆明市污水處理廠出水水質評價 [J]. 中國環境科學, 2013,33(6):1113-1119.

[18] 何 靜,陳錫康.水資源影子價格動態投入產出優化模型研究[J]. 系統工程理論與實踐, 2005,25(5):49-54.

[19] 陳渙壯.污水處理廠投資及運營研究 [D]. 湖南大學, 2004.

[20] 譚 雪,石 磊,馬 中,等.基于污水處理廠運營成本的污水處理費制度分析——基于全國 227個污水處理廠樣本估算 [J].中國環境科學, 2015,35(12):3833-3840.

[21] 蔣 勇,阜 葳,毛聯華,等.城市污水處理廠運行能耗影響因素分析 [J]. 北京交通大學學報:自然科學版, 2014,38(1):33-37.

[22] 陳宏儒.城市污水處理廠能耗評價及節能途徑研究 [J]. 西安:西安建筑科技大學, 2009.

[23] 成官文,朱宗強,徐子涵,等.廣西城鎮污水處理廠建設和運行的現狀分析 [J]. 環境工程學報, 2013,7(7):2579-2586.

[24] 梁東花.基于網絡分析法的云南省小城鎮污水處理工藝的評價研究 [D]. 昆明:昆明理工大學, 2014.

[25] 張 揚,李子富,宋英豪,等.改進Orbal氧化溝工藝污水處理廠脫氮效果研究 [J]. 中國環境科學, 2012,32(8):1461-1466.

[26] 王穎懿.改進ICEAS工藝在污水處理中的應用 [D]. 上海:華東理工大學, 2014.

[27] 馬魯銘,王云龍,劉志剛,等.南方農村生活污水處理目標及工藝模式探討 [J]. 中國環境科學, 2013,33(1):118-122.

[28] 侯亞輝.A～2/O、倒置A～2/O和前置缺氧A～2/O工藝處理城市污水比較研究 [D]. 鄭州:鄭州大學, 2010.

[29] 曾 薇,李 磊,楊瑩瑩,等.A2O工藝處理生活污水短程硝化反硝化的研究 [J]. 中國環境科學, 2010,30(5):625-632.

[30] 王西琴,高 偉,張 遠.基于控制單元的農村生活污水處理優化模型 [J]. 中國環境科學, 2015,35(9):2835-2842.

[31] 宋連朋,魏連雨,趙樂軍,等.我國城鎮污水處理廠建設運行現狀及存在問題分析 [J]. 給水排水, 2013,39(3):39-44.

[32] 張英民,盧文洲,王 煒,等.農村生活污水處理工程技術方案優選研究 [J]. 中國環境科學, 2013,33(S1):210-214.

An inexact two-stage stochastic programming model for optimization of sewage treatment technology.

WANG Jian, FU Zheng-hui, GUO Huai-cheng*
(College of Environmental Science and Engineering, Peking University, Beijing 100871, China). China Environmental Science, 2017,37(1)：108～115

In order to solve the existing problems about one-sidedness, subjectivity and uncertainty in optimization methods of sewage technology, this study maximized the benefits of the environment and society, and developed an inexact two-stage stochastic programming model to choose the optimized treatment technology and to calculate their capacities for the increased regional sewage. After the model was applied in Dianchi-Panlongjiang watershed, the results indicated that the combination of sewage treatment technology was the best choice comparing with choosing one specific technology. Anaerobic-Anoxic-Oxic(A2/O) had obvious advantages in a large scale due to the low cost of operation and investment. Meanwhile,Intermittent Cycle Extended Aeration(ICEAS) was more suitable to be applied in small emission areas, and it had a deeper removal efficiency of pollutant than A2/O and oxidation ditch(OD).

inexact two-stage stochastic programming；uncertainty；sewage treatment technology；optimization model；Dianchi watershed

X505

A

1000-6923(2017)01-0108-08

王 劍(1992-),男,浙江溫州人,北京大學碩士研究生,主要研究方向為水環境學、環境規劃與管理.

2016-04-22

國家水體污染控制與治理科技重大專項(2013ZX07102-06)

* 責任作者, 教授, hcguo@ pku.edu.cn