基于核方法的虛擬樣本構造

劉鵬飛，何良華

(同濟大學 電子與信息工程學院，上海 201804)

基于核方法的虛擬樣本構造

劉鵬飛，何良華

(同濟大學 電子與信息工程學院，上海 201804)

樣本不平衡問題已經成為機器學習領域的研究熱門。虛擬樣本生成方法是一種重要的解決樣本不平衡問題的方法，它通過線性生成少數類樣本來實現。在以往的大多數研究工作中，虛擬樣本的生成是在原始的特征空間中進行的，樣本通常處于線性不可分的狀態，將會導致生成的虛擬樣本丟失幾何特性。因此，文章提出了一種基于核方法的虛擬樣本構造方法，虛擬樣本在線性可分的核空間中生成。

樣本不平衡；支持向量機；虛擬樣本；核方法

0 引言

對不平衡樣本的學習一直是機器學習領域的熱點問題。樣本不平衡問題的主要難點在于以往的分類算法大多以樣本分布平衡為前提，導致了分類結果往往偏向于多數類樣本[1]。

為解決樣本不平衡條件下的分類問題，人們提出了很多應對方法。其中，構造虛擬樣本作為基于數據層面的一種策略已經成為一種主流的處理方法[2]。構造虛擬樣本方法通過生成少數類虛擬樣本來平衡樣本分布，從而減少因樣本分布不平衡帶來的影響。CHAWLA N V等人提出了Synthetic Minority Oversampling Technique (SMOTE)[3],利用相鄰樣本的特征相似性，通過對相鄰少數類樣本進行插值構造的方法生成虛擬樣本。SMOTE在很多領域表現出了出色的性能，很多研究者在SMOTE的基礎上提出了改進，如HAN H等人提出了Borderline-SMOTE[4]，只選取分界面邊界附近的少數類樣本進行SMOTE生成。HE H等人提出了Adaptive synthetic sampling approach for imbalanced learning(ADASYN)[5]，根據不同的分布密度對不同區域的少數類樣本生成不同數量的虛擬樣本。

然而，如SMOTE等以往的工作，對少數類樣本的構造都是在原始的低維空間中進行的。構造少數類樣本通常使用線性組合其他的少數類樣本進行生成，而低維空間中的樣本往往處于線性不可分的狀態，這可能導致新生成的虛擬樣本丟失該類的幾何特性。因此，在線性可分的空間中對樣本進行線性生成是一種更加適合的選擇，一方面線性可分的條件使得分類學習更加容易，另一方面，線性可分空間保證了新生成的樣本的幾何分布更加契合原始的樣本空間。支持向量機(Support Vector Machine，SVM)[6]算法將線性不可分的樣本映射到線性可分的更高維空間中進行分類。因此，本文結合SVM，通過在高維線性可分空間中構造虛擬樣本，從而提高分類器在樣本不平衡條件下的分類性能。

1 SVM算法

本文期望在一個線性可分的空間中構造虛擬樣本，而現實生活中大多數數據都是線性不可分的，因此需要將數據從原始空間映射到線性可分空間中。而SVM正是這種算法，通過核方法將原始空間中樣本映射到一個高維空間中，在這個高維空間中樣本是線性可分的。下面將介紹所涉及到的SVM相關知識。

1.1 SVM基本公式

當樣本處于線性可分的情況時，SVM的決策公式如下：

SVM(x)=sign()+b

(1)

w則通過下式得到:

(2)

其中αi是SVM的對偶目標函數中的拉格朗日乘子：

(3)

從式(2)中可以得知，w僅僅由那些αi>0的項組成。這些αi>0的樣本xi對應到SVM中被稱為支持向量(SupportVector)，它們對SVM分界面的構建起到了決定性的作用。因此對于樣本不平衡的分析問題，更多地關注于作為支持向量的樣本。

1.2 SVM中的核函數

當樣本處于線性不可分的情況時，SVM首先使用核函數將樣本映射到一個高維線性可分的空間，然后再利用上述公式進行分類。

核函數與樣本特征之間的關系表達式如下：

F=<φ(xi),φ(xj)>F=K(xi,xj)H

(4)

其中φ是映射函數，它將處于原始特征空間H(Hilbert，希爾伯特空間)的樣本映射到高維空間F，在高維空間中樣本線性可分程度更大。通過φ，一個低維空間中xi被映射到高維空間中的zi=φ(xi)。同時，在映射之后內積的計算復雜度并沒有增加，通過核函數的技巧計算仍然可以在低維空間中進行。

將核函數應用到1.1節中，SVM的決策函數將變為：

SVM(x)=sign(F+b)

(5)

α通過對偶目標函數得到：

(6)

從式(6)中可以得知，求解一個SVM模型只需輸入樣本兩兩之間的核函數值。這些兩兩的核函數值可以用矩陣的形式來表示，并且稱之為核矩陣。

2 基于核方法的虛擬樣本構造

核方法有效地將低維空間中的線性不可分的樣本映射到高維空間中，使得樣本線性可分程度大大增加。在線性可分的高維空間中構建決策面更加簡單，同時對于樣本的線性生成也能保持相關的幾何特性，因此本文的虛擬樣本構造方法是基于這樣的核空間。同時SVM算法作為利用核方法的典型代表，本文選取SVM算法對樣本進行分類。

2.1 虛擬樣本的表示

在SVM映射后的核空間(即高維空間)中的樣本通常形式會比較復雜，甚至在常用的高斯核映射后的樣本具體特征都不可知(高斯核將樣本映射至無窮維度)，所以構建虛擬樣本不能基于具體的單獨的樣本。

從1.1節中的式(6)得知，求解一個SVM模型只需關注樣本兩兩之間的核函數值。所以對于高維空間中具體的單獨樣本過于復雜的問題，可以把高維空間中具體的虛擬樣本替換為該虛擬樣本與其他所有樣本的核函數值。

通過插入給定兩個高維空間中樣本的中值來代表一個虛擬樣本的生成：

(7)

z*表示由已知高維空間中的樣本z1和z2生成的虛擬樣本，要知道在高維空間中這些樣本都是不可知的，因此本文使用z*與所有其他樣本的核函數值(也即高維空間中的內積)來表示虛擬樣本：

Kz*,x=

(8)

2.2 虛擬樣本的構造

2.1節中已經將虛擬樣本的表示轉換成了虛擬樣本與其他樣本之間的核函數值，因此虛擬樣本的構造問題也就轉換成了如何求解它們的核函數值。

利用內積空間中線性性質，可以將式(8)計算如下：

(9)

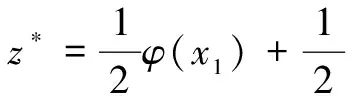
(10)

生成一個樣本時，核矩陣從N階矩陣KM1擴展到N+1階矩陣KM2。

2.3 構造源的選取

插值生成虛擬樣本所需要的兩個樣本稱為構造源，生成不同的虛擬樣本需要不同的構造源，本節主要討論對于構造源的選取。

圖1 SVM中不同樣本分布示意圖

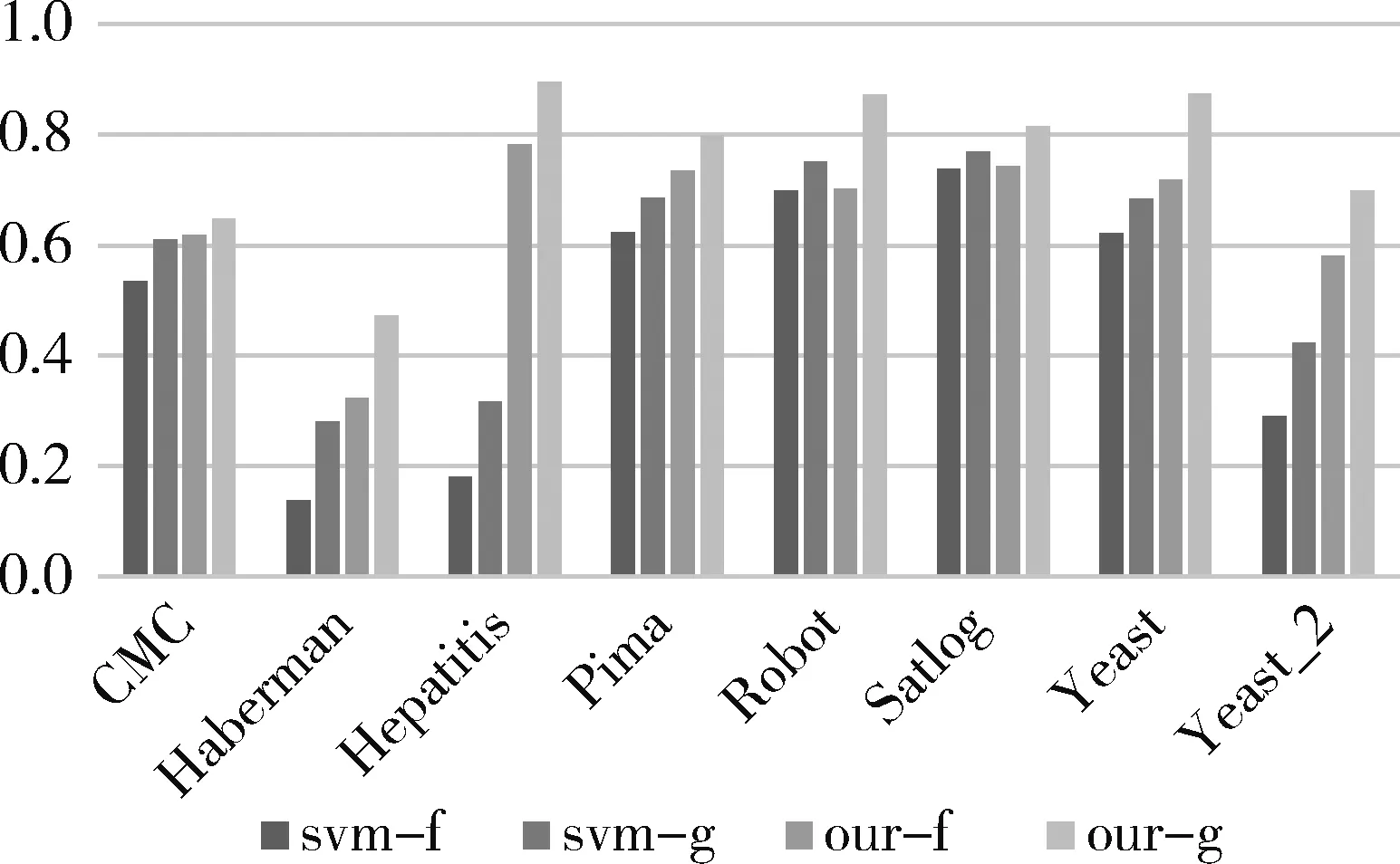
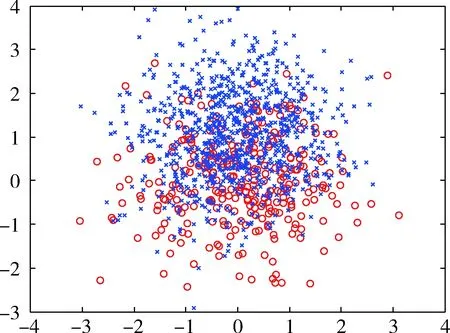
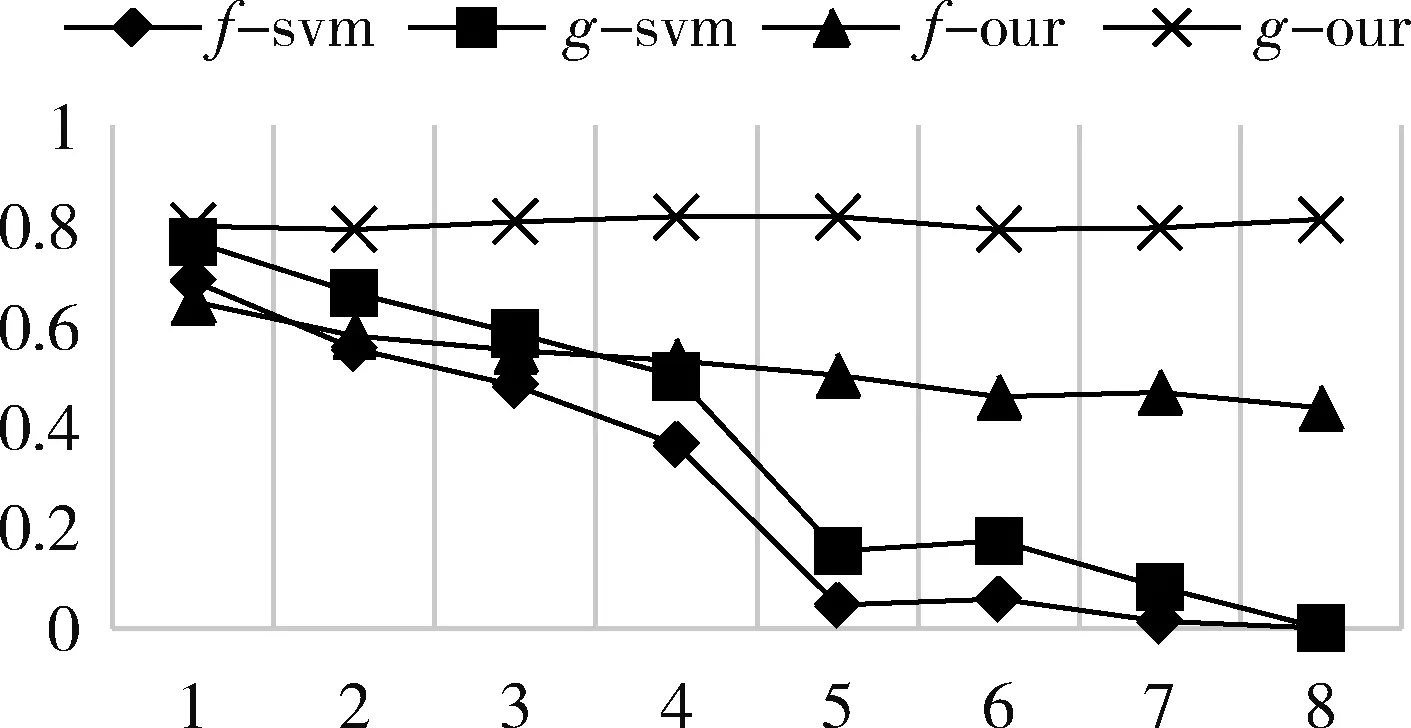
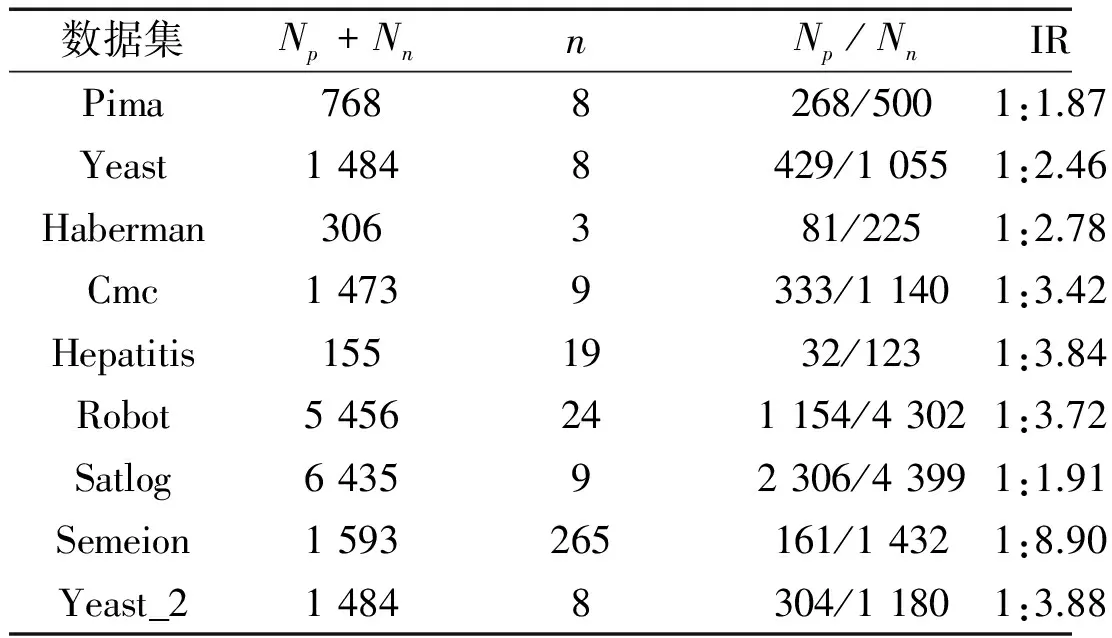
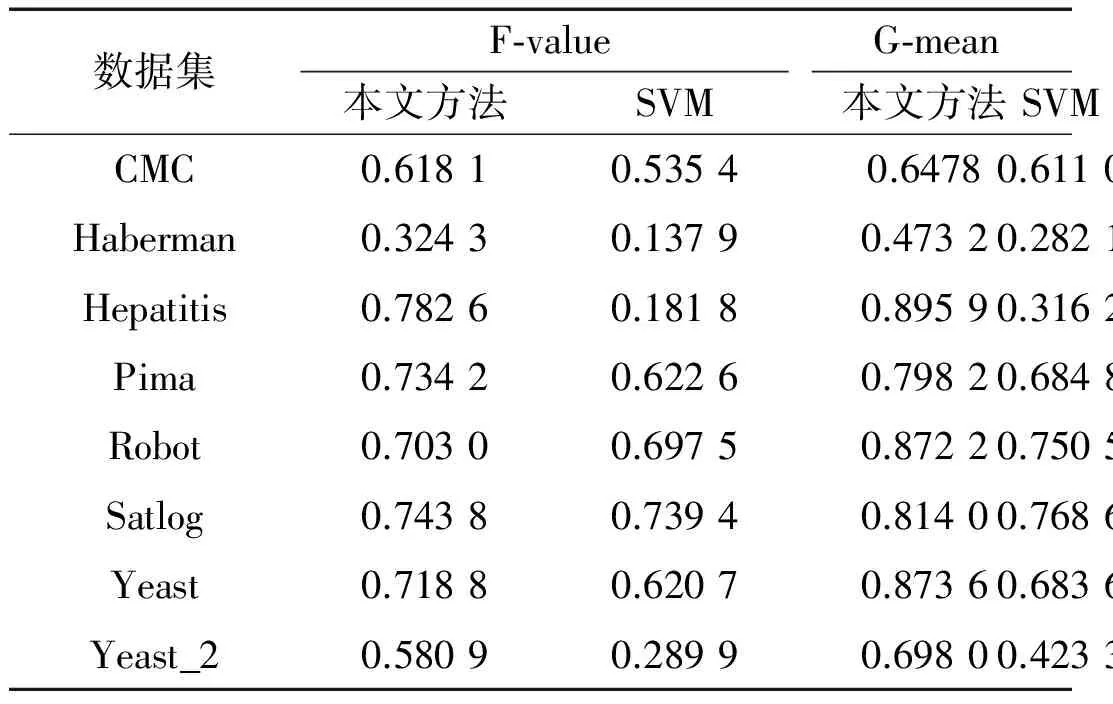
圖1中為SVM分類后不同類別的樣本分布示意，圖中有兩類樣本，中間實線表示SVM分類決策面，實線兩旁的虛線代表兩類樣本的支撐界面。對于單獨的一類樣本來說，分類后的樣本點可以分為三類：第一類介于支撐界面內側，對應到式(5)中該類樣本點的αi=0，這類樣本點對于SVM分界面的構建沒有任何影響，甚至對該類樣本進行增減后都不會影響SVM分界面；第二類處于支撐界面上，其0<αi

對這三類樣本點都進行了相應的虛擬樣本的構造，得到的結論為：只有選取αi=C的第三類樣本作為構造源生成后才會改變SVM分界面。

3 實驗結果

本節將從兩個實驗來驗證本文所提出方法的有效性。實驗將使用本方法后的分類結果與原始的SVM分類結果進行對比。實驗1使用人造數據集作為數據，實驗2使用UCI真實數據集。

3.1 人造數據集

為了驗證提出方法的有效性，實驗將在人造數據集上對比原始SVM分類結果與構造虛擬樣本后的分類結果。構造虛擬樣本時，樣本生成數量為多數類樣本與少數類樣本數量的差值，構造源選取αi=C的樣本，同時，生成方式為隨機生成。

實驗使用的數據集由兩個高斯分布構成，分別代表兩類樣本的分布，以其中一類為少數類樣本，另一類為多數類樣本。不同不平衡率的數據集是以少數類為基數，按照比例增加多數類樣本形成的。圖2為訓練樣本的分布，圖3為不同不平衡率情況下SVM與本文方法的對比。圖3橫軸表示不平衡率，縱軸表示性能指標，其中f代表F-value指標，g代表G-mean指標，這兩個指標都能比較好地考量不平衡條件下地分類性能。

圖2 人造數據集樣本分布

圖3 不同不平衡率下SVM與本文方法對比

從圖3中可以看到隨著不平衡率的上升，SVM在F-value和G-mean下的性能顯著下降，而本文的方法在1～8的不平衡率下性能只有輕微下降，并且高于SVM。

3.2 UCI數據集

本節實驗采用UCI中部分數據集作為真實數據集，每個數據集的詳細信息如表1所示。Np、Nn分別代表少數類樣本和多數類樣本的數量，n代表樣本的特征數，IR表示數據集的不平衡率。

表1 UCI數據集信息

實驗結果見表2和圖4。表2中列出了SVM與本文方法的F-value和G-mean值，而圖4對比了它們的性能。從圖4可以看出，本文方法相比于SVM在F-value和G-mean兩個指標下都有明顯的提升。

表2 UCI數據集上性能對比

4 結論

本文提出了一種新的在核空間中構造虛擬樣本的方法來解決樣本不平衡問題。在SVM的理論中分析了構造

圖4 UCI數據集上分類結果對比

虛擬樣本的原理，同時在試驗中對所提出的方法的有效性進行了驗證。在具有不同不平衡率的人造數據集以及現實生活中的真實數據集中，基于核方法的虛擬樣本構造方法的表現均優于原始的SVM。

[1] BORDES A, ERTEKIN S, WESTON J, et al. Fast kernel classifiers with online and active learning[J]. Journal of Machine Learning Research, 2012, 6(6):1579-1619.

[2] HE H, BAI Y, GARCIA E A, et al. ADASYN: adaptive synthetic sampling approach for imbalanced learning[C]. 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence). IEEE, 2008: 1322-1328. [3] CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2011, 16(1):321-357.

[4] HAN H, WANG W Y, MAO B H. Borderline-SMOTE: a new over-sampling method in imbalanced data sets learning[C].International Conference on Intelligent Computing, Springer Berlin Heidelberg, 2005: 878-887.

[5] HE H, GARCIA E A. Learning from imbalanced data[J]. IEEE Transactions on Knowledge & Data Engineering, 2009, 21(9):1263-1284.

[6] VAPNIK V. The nature of statistical learning theory[M]. Springer Science & Business Media, 2013.

Synthetic sample construction based on kernel method

Liu Pengfei，He Lianghua

(College of Electronics and Information Engineering, Tongji University, Shanghai 201804, China)

Learning from imbalanced data is a popular problem in machine learning. Synthetic over-sampling method is one of important approaches by generating linear synthetic minority class samples. While in most previous works, synthetic samples are generated in original feature space where samples are linear non-separable, which leads to the loss of geometrical relation between samples. Therefore, in this paper, a new oversampling method called kernel-based oversampling method is proposed, samples are generated in kernel space where samples in this space are linear separable.

imbalanced data; support vector machine; synthetic sample; kernel method

TP181

A

10.19358/j.issn.1674- 7720.2017.03.016

劉鵬飛，何良華.基于核方法的虛擬樣本構造[J].微型機與應用，2017,36(3)：52-54,58.

2016-10-15)

劉鵬飛(1991-)，男，通信作者，碩士研究生，主要研究方向：認知與智能信息處理。E-mail:1433239@tongji.edu.cn。

何良華(1977-)，男，博士，教授，主要研究方向：認知與智能信息處理。