算法設計類課程分層大案例庫設計與構建方法研究

盧 玲，曾慶森

（重慶理工大學 計算機科學與工程學院，重慶 400050）

算法設計類課程分層大案例庫設計與構建方法研究

盧 玲，曾慶森

（重慶理工大學 計算機科學與工程學院，重慶 400050）

分析算法設計類課程實踐教學案例存在規(guī)模小、背景簡化、數(shù)據(jù)形態(tài)單一、不利于觀察算法的時空效率問題，提出以數(shù)據(jù)結構課程為對象，建立分層大案例庫的研究目標，闡述大案例的特點并結合具體教學實踐介紹大案例庫的設計與構建方法。

算法設計；教學案例；數(shù)據(jù)形態(tài)；案例庫

1 背 景

算法設計類課程包括程序設計基礎、數(shù)據(jù)結構、算法分析與設計、面向對象程序設計等，是普通高校計算機各專業(yè)及部分信息類非計算機專業(yè)重要的專業(yè)基礎課[1]。課程受眾廣泛，其受眾關系如圖1所示。從圖1可見，數(shù)據(jù)結構、算法分析與設計課程由于具有邏輯性強、抽象性高[2]的特點，在課程體系中承上啟下，是將學生的綜合能力從實踐向理論層面提升的重要環(huán)節(jié)。

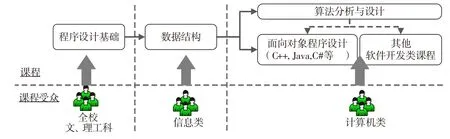
圖1 算法設計類課程及其受眾關系圖

目前，從計算科學的應用現(xiàn)狀看，隨著云計算等分布式計算平臺的發(fā)展，數(shù)據(jù)規(guī)模不斷擴大，以大數(shù)據(jù)為背景的數(shù)據(jù)分析、信息檢索等應用已成為計算科學領域的重要熱點。這類應用面向具有超大規(guī)模、異構、多源、多維特征的數(shù)據(jù)，其研究往往需要較強的理論基礎和創(chuàng)新能力。這些具有大數(shù)據(jù)特征的現(xiàn)實問題，對學生的分析能力和研究創(chuàng)新能力提出了比以往任何工程項目都更高的新要求。在培養(yǎng)研究創(chuàng)新能力方面，算法設計類課程是重要的支撐。課程通過學習算法理論為學生的模型抽象能力[3]和創(chuàng)新能力的形成奠定基礎。為使抽象的算法具體化、形象化[4]，課程往往設計實驗案例并輔以課程設計等綜合實踐。從教學實踐看，現(xiàn)有實驗案例多以驗證性、小型綜合性實驗為主。這些實驗多對問題背景設置約束條件，將問題規(guī)模限制在一定范圍之內(nèi)。實驗使用的測試數(shù)據(jù)不是真實數(shù)據(jù)，其數(shù)據(jù)規(guī)模小、數(shù)據(jù)結構單一。這使得學生常常對算法的應用場景產(chǎn)生疑惑，難以理解算法在真實環(huán)境中的適用性及效果。由于這一階段的學生缺少工程實踐經(jīng)驗，難以預期真實環(huán)境的數(shù)據(jù)規(guī)模及數(shù)據(jù)形態(tài)，對算法的時間、空間性能缺乏真實感受，使所學算法分析理論變成紙上談兵，無法將基礎算法規(guī)律化[5]，出現(xiàn)理論與實踐脫節(jié)，學生雖學而不以為然的問題。

可見，傳統(tǒng)教學中基于虛擬、小型、受約束數(shù)據(jù)的案例，逐漸與大數(shù)據(jù)背景下的工程實踐問題脫節(jié)，成為制約分析和研究能力的瓶頸，是算法設計類課程面臨的現(xiàn)實問題。在這樣的背景下，我們以數(shù)據(jù)結構課程為研究對象，提出對課程的案例庫進行梳理和更新，設計具有多種數(shù)據(jù)規(guī)模、多元數(shù)據(jù)形態(tài)的分層大案例庫;并提出針對分層大案例庫的多元考核體系，使大案例庫的應用具有可行性和良好的可操作性。

2 分層大案例庫結構設計

1）大案例及其特點。

我們把大案例定義為具有一定規(guī)模、一定邏輯結構、一定形態(tài)的數(shù)據(jù)處理實例。大案例中的“大”體現(xiàn)為數(shù)據(jù)規(guī)模、數(shù)據(jù)元素的形態(tài)是復雜的，意味著案例中將要處理數(shù)據(jù)的未知性，包括規(guī)模未知、形態(tài)未知、結構未知。其“一定規(guī)模”是指數(shù)據(jù)量小規(guī)模、數(shù)據(jù)量中規(guī)模、數(shù)據(jù)量大規(guī)模。“一定邏輯結構”是指數(shù)據(jù)具有線性、樹形、圖形結構。“一定形態(tài)”是指數(shù)據(jù)元素包括簡單類型（整型、浮點型、字符型）、復雜類型（文本、圖像、聲音）。結合這3個“一定”對大案例進行定義和篩選，并將案例庫進行組織及結構分層，由此得到如圖2 所示的分層案例庫邏輯結構。

如圖2所示，大案例庫是一個3維結構，具有“數(shù)據(jù)規(guī)模層次”“數(shù)據(jù)形態(tài)層次”“邏輯結構層次”3個維度。每個維度上分別按數(shù)據(jù)規(guī)模、數(shù)據(jù)形態(tài)、邏輯結構進行層次劃分。可見，大案例庫中的每一個案例是3維空間中的1個點，如圖2所示的大案例k。

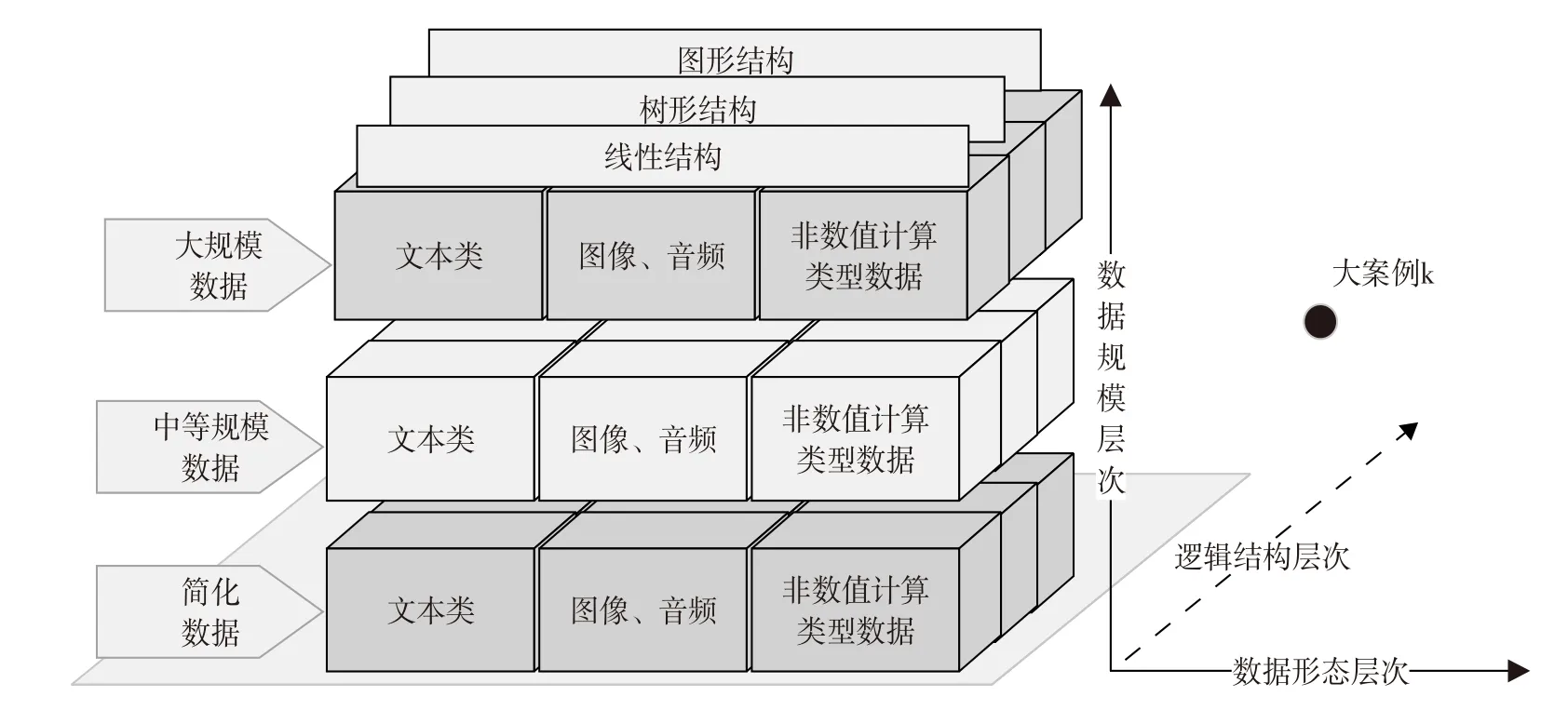
圖2 分層大案例庫示意圖

2）大案例設計的重點。

大案例設計的重點在于突出數(shù)據(jù)處理實例中數(shù)據(jù)的不可預知性、不可觀察性。以數(shù)據(jù)結構課程的“哈夫曼樹及哈夫曼編碼”為例，傳統(tǒng)實驗案例中，通常給定字符頻度或分布（通常為整型或浮點型數(shù)據(jù)），要求學生基于給定的分布進行實驗;在測試哈夫曼編碼時，一般也以給定的文本為測試數(shù)據(jù)。這種案例設計限定了字符的范圍和分布，限定了測試數(shù)據(jù)的規(guī)模。雖然這些限定簡化了問題的復雜度，使學生能快速掌握算法原理，但從算法分析的角度，問題數(shù)據(jù)及其規(guī)模的簡化使學生難以對真實數(shù)據(jù)形成認知。由于算法的時空指標及算法策略的優(yōu)劣，只有在測試數(shù)據(jù)達到一定規(guī)模對計算機的存儲形成壓力時才能觀察到，進而迫使學生考慮算法的適用性問題，主動尋求優(yōu)化方案。簡化的案例背景及數(shù)據(jù)使某些算法評估指標不易呈現(xiàn)，難以激勵學生對算法優(yōu)劣進行主動評價。實踐中發(fā)現(xiàn)，大多數(shù)學生對算法優(yōu)劣的理解源于書本知識，很少通過實驗主動觀察和體驗到。由此，針對“哈夫曼編碼問題”設計的大案例分為L1～L3三層，描述如下：

L1：給定訓練文本，限定字符范圍，包括大小寫英文字符、常見標點符號（逗號，句號）。

L2：自行搜集訓練文本（文本數(shù)＜1 000篇），手動整理字符，保留大小寫英文字符、常用標點符號。

L3：自行搜集訓練文本（文本數(shù)＞1 000篇），保留全部（多種）字符、多種標點符號。

在案例級別L3上，由于訓練文本數(shù)擴大，字符范圍未知，需要對哈夫曼樹的存儲設計進行可行性分析和論證。對所生成的哈夫曼編碼，由于符號數(shù)量多，難以進行人工觀測，只能通過編程計算哈夫曼編碼與其他（如定長編碼）編碼的電文壓縮比，由此促使學生為尋求合理的解決方案，運用多種技術對數(shù)據(jù)進行觀察和分析，展開研究性學習。

3 大案例庫構建的關鍵問題

如前所述，大案例處理的數(shù)據(jù)應具有一定的未知性和不可觀測性。可將這種未知性分為3個維度：規(guī)模未知、形態(tài)未知、邏輯結構未知，基于此，建立大案例庫需解決4個關鍵問題。

3.1 合理定義大案例數(shù)據(jù)的規(guī)模

可將大案例的數(shù)據(jù)規(guī)模定義為簡化數(shù)據(jù)、中等規(guī)模數(shù)據(jù)、大（在現(xiàn)有實踐條件之內(nèi)）規(guī)模數(shù)據(jù)。實踐中可分3階段進行案例實施：

（1）STEP 1：簡化數(shù)據(jù)。使算法快速實施;形成簡化數(shù)據(jù)的測試報告;屬于封閉答案的問題，其測試結果及算法策略是確定的。

（2）STEP 2：中等規(guī)模數(shù)據(jù)。例如將排序數(shù)據(jù)規(guī)模設置為5 000～5 000 000整數(shù)，要求進行多組數(shù)據(jù)規(guī)模、多種算法策略的測試，并以數(shù)據(jù)表的形式記錄測試的時空開銷，最終形成中等規(guī)模數(shù)據(jù)的測試報告;屬于開放答案的問題，包括多樣的測試結果及多種算法優(yōu)化策略。

（3）STEP 3：大規(guī)模數(shù)據(jù)。例如將排序數(shù)據(jù)規(guī)模設置為5 000 000整數(shù)以上，對由此可能產(chǎn)生的存儲異常及時間代價問題，要求采取合理的方法進行解決，最終形成大規(guī)模數(shù)據(jù)的測試報告;屬于開放答案的問題，包括無解、多種測試結果及多種存儲方式、多種算法優(yōu)化策略。

由此可見，基于大案例展開的實踐總是包含多數(shù)據(jù)規(guī)模、多種算法的測試。基于此進行對比分析形成分析報告，有助于學生主動發(fā)現(xiàn)和解決問題，對其研究能力形成有針對性的引導。

3.2 選取具有多種形態(tài)的數(shù)據(jù)

一般數(shù)據(jù)處理問題中的信息包括文本、圖像、聲音，這些信息的編碼可能表現(xiàn)為整型、浮點型，在非數(shù)值計算方面的數(shù)據(jù)則具有更為復雜的表現(xiàn)形式，如計算機人機對弈中的一次棋盤狀態(tài)。對此，可針對不同類型的數(shù)據(jù)設置案例，具體有：①文本類：包括中文、英文長文本（如新聞文本）、短文本（如網(wǎng)絡評論性）文本;②圖像和音頻類：包括彩色、灰度、二值圖像、各種音頻信號等;③非數(shù)值計算類數(shù)據(jù)：如地圖、棋盤等。

上述數(shù)據(jù)具有多樣、規(guī)模各異且規(guī)模不確定的特點（如新聞文本的長度常常是無法預知的）。在進行案例設計時，可提供模擬（簡化）數(shù)據(jù)、仿真數(shù)據(jù)、真實數(shù)據(jù)3類。其中，真實數(shù)據(jù)可從實際工程項目中獲取，仿真數(shù)據(jù)可基于真實數(shù)據(jù)進行一定的人工調(diào)整和簡化。由于仿真數(shù)據(jù)和真實數(shù)據(jù)具有規(guī)模大的特點，難以進行人工觀測，將促使學生運用編程技術、算法設計方法，以尋求觀測數(shù)據(jù)的最佳途徑，從而形成啟發(fā)式的主動學習。另外，還可要求學生自行進行數(shù)據(jù)采集和整理，從數(shù)據(jù)采集、整理方面，對學生進行訓練。

3.3 選取具有多樣邏輯結構的案例

在算法設計中，邏輯結構通常指數(shù)據(jù)元素具有線性、樹形、圖形的邏輯關系，在大案例庫中應包含具有這幾類邏輯結構的案例。當數(shù)據(jù)規(guī)模較小時，數(shù)據(jù)的邏輯結構是易于觀測和判斷的;在大案例中，由于數(shù)據(jù)規(guī)模增大，數(shù)據(jù)元素間的邏輯關系變得難以感知，無法進行主觀臆測。這一方面要求學生借助經(jīng)驗進行分析，例如分析認為人機對弈的棋盤格局形成了樹形結構;另一方面，也需要通過一定的策略對數(shù)據(jù)的邏輯結構進行學習和挖掘，例如對數(shù)值化的圖形結構，發(fā)現(xiàn)其是有向關系還是無向關系等。通過這種分析，也可以促使主動學習模式的形成。

3.4 設計多元考核體系

分層大案例庫具有豐富的層次性，形成多樣化、有吸引力的實驗內(nèi)容，可激勵學生展開主動學習。為便于進行自主學習，同時對教學產(chǎn)生實時反饋，有必要設計相應的評價機制，以保證大案例庫應用的可行性和可操作性。針對案例庫分層、多樣的特點，評價體系也應是多層次、多元化的。另外，為能有效反饋教學，評價體系應是定量與定性評價相結合的多元系統(tǒng)，具有良好的可操作性。例如展開形式多樣的測驗，持續(xù)開展算法設計系列競賽并以此作為評價指標等。同時也應結合定性評價，例如以項目小組的方式展開實驗，進行團隊協(xié)作能力、溝通能力等評價。

我們在教學實踐中運用的評價指標，與傳統(tǒng)實驗差別最大之處在于實驗報告環(huán)節(jié)。由于本科教學往往更注重應用能力培養(yǎng)，所以傳統(tǒng)的實驗報告多以描述實驗過程和實驗結論為主。大案例庫的層次性及數(shù)據(jù)規(guī)模各異性，可能使實驗結論也是各異的，這是展現(xiàn)學生分析能力的良好觀測點。實踐中，可啟發(fā)學生綜合運用圖、表、偽代碼等多種手段，觀測實驗結果，編寫分析報告。對分析報告的質(zhì)量，尤其是分析部分的內(nèi)容進行重點評價，由此將學習的注意力從單純追求實驗結果轉移到關注實驗過程，為培養(yǎng)研究創(chuàng)新能力打下基礎。

4 結 語

上述分層大案例庫的設計及構建方法是結合數(shù)據(jù)結構課程的教學實踐提出的，是在現(xiàn)有課程建設的基礎上對實踐教學環(huán)節(jié)的細化和深人求精。大型、綜合型案例設計，與大數(shù)據(jù)背景下對研究型、創(chuàng)新性計算機本科人才培養(yǎng)的要求密切相關，是在計算機應用型人才培養(yǎng)與強化理論研究、鼓勵思維創(chuàng)新有效結合方面進行的一次有益探索。將大案例庫運用于我校計算機類各專業(yè)的數(shù)據(jù)結構課程教學，實踐中取得了顯著的效果。近3年來，我校計算機類本科學生廣泛參與各類學科競賽，如CCF中文信息評測、ASC國際大學生超算競賽、中國大數(shù)據(jù)創(chuàng)新創(chuàng)業(yè)大賽等，參與學生面逐年擴大，這與教學中注重啟發(fā)式、研究式的學習是密切相關的，從一定程度上驗證了數(shù)據(jù)結構課程的教學效果。由于數(shù)據(jù)結構課程理論與實踐兼?zhèn)洌哂衅渌惴愓n程的普遍特征，因此分層大案例庫的設計與構建對其他算法設計類課程也具有良好的借鑒意義。后續(xù)將在如何保證多種案例，尤其是較難大案例實施的有效性方面展開進一步的研究。

[1] 陳越, 何欽銘. 數(shù)據(jù)結構MOOC實踐[J]. 中國大學教學, 2015(12): 46-50.

[2] 霍玲玲, 王智, 孫江. 數(shù)據(jù)結構教學方法的研究[J]. 計算機教育, 2015(2): 73-76.

[3] 陳欲強, 周國軍, 吳慶軍, 等. 非重點院校的數(shù)據(jù)結構課程教學改革[J]. 計算機教育, 2015(14): 52-55.

[4] 王丹, 付利華, 杜金蓮. 算法分析與設計課程中的”三化一體”教學方法[J]. 計算機教育, 2016(7): 120-122.

[5] 代文征, 楊勇, 蔣文娟. 數(shù)據(jù)結構程序庫建設[J]. 計算機教育, 2016(6): 70-71.

（編輯：郭田珍）

1672-5913(2017)01-0143-04

G642

2014重慶市研究生教育教學改革項目（yjg143011）；2015重慶理工大學高等教育教學改革研究項目（2015YB23）。

盧玲，女，副教授，研究方向為機器學習、信息檢索、并行計算，ll@cqut．edu．cn。