原子干涉磁力儀信號鑒頻優(yōu)化算法設計
張笑楠,孫曉潔,寇 軍,魏宗康,任 章
(1.北京航空航天大學自動化科學與電氣工程學院,北京 100191;2.北京航天控制儀器研究所,北京 100039)
原子干涉磁力儀信號鑒頻優(yōu)化算法設計
張笑楠1,2,孫曉潔2,寇 軍2,魏宗康2,任 章1
(1.北京航空航天大學自動化科學與電氣工程學院,北京 100191;2.北京航天控制儀器研究所,北京 100039)
原子干涉磁力儀是通過確定CPT鑒頻信號曲線峰值所對應的頻率值來計算磁場強度值的.信號峰值定位鎖定算法的搜索速度、準確度和穩(wěn)定性直接影響磁力儀的分辨率和響應速度.常見的斜率算法只適用于小步長的搜索,定位速度慢,鎖定狀態(tài)的穩(wěn)定性差.針對此問題,通過建立磁力儀鑒頻信號曲線數(shù)學模型,設計了PI跟蹤控制算法和快速鎖定算法兩種優(yōu)化算法,并經仿真實驗對比了性能.研究結果表明:3種算法中快速鎖定算法不僅受初始搜索步長的影響小,而且峰值定位速度最快,穩(wěn)定性好,對于原子干涉磁力儀系統(tǒng)的性能提高有很大的應用價值.
原子干涉磁力儀;CPT鑒頻信號曲線;峰值定位鎖定;優(yōu)化算法
原子干涉磁力儀是基于相干布居囚禁(coherent population trapping,CPT)原理工作的.CPT是激光光場與原子相互作用時發(fā)生量子干涉的結果,是一種量子干涉現(xiàn)象.原子的磁子能級在磁場為零時都是簡并的.當存在外磁場的情況下原子能級會發(fā)生塞曼分裂.當兩個與原子作用的激光場的頻率差與原子基態(tài)超精細子能級的劈裂間距精確匹配時,原子被束縛在這兩個能級之間的無相互作用的暗態(tài)上.這個現(xiàn)象在激光強度變化上的表現(xiàn)為吸收光譜中出現(xiàn)非常窄的透射信號.通過對該光譜信號對應頻率的測量和計算可以得到外磁場的強度值[1-3].
傳統(tǒng)的光譜信號鑒頻方法是通過求取信號的一次微分來實現(xiàn)的,也就是將信號的幅值信息轉化成斜率信息進行鑒別.由于單個信號峰的斜率是由小到大連續(xù)變化的,峰值點對應的斜率為零值,所以通過數(shù)值計算定位零值所對應頻率就可以達到鑒頻的目的.目前國內外CPT測磁實驗中最常用的方案是使用鎖相放大器和濾波電路模塊獲得光功率信號的一次微分曲線[4].該方案如果使用小型電路和程序來替代精密儀器嵌入小型樣機中,就會受計算速度的限制,并且對數(shù)據(jù)存儲量的要求也較大,穩(wěn)定性不高.所以本文從提高曲線鑒頻計算速度、數(shù)據(jù)量和穩(wěn)定性方面來進行優(yōu)化算法的設計.
1 原子干涉磁力儀信號數(shù)學模型
由于原子干涉磁力儀是通過對原子干涉信號進行精確分析來計算相應的磁場強度的,為了深入分析信號的處理方法,需要首先建立鑒頻信號的數(shù)學模型.原子干涉過程中原子系統(tǒng)的演化可以用原子密度矩陣的形式表達[5-6].在此基礎上將光量子傳感器感應到的與原子作用的激光光強信號分為3個組分,分別是激光器射入原子氣室的入射激光功率Pin,原子氣室吸收的光功率Pa和CPT信號.傳感器內的光電探測器感應到光功率信號表示為Pout,建立它們之間的關系模型如下.
Pout=Pin-Pa-Pcpt,
(1)
式中,
(2)
(3)
(4)
(5)
式(2)中的w1和ωa分別為激光器實際輸出頻率和設定頻率;式(3)中的Г為原子激發(fā)態(tài)到基態(tài)退相干;λ為激光器輸出激光光波長;n為原子氣室內充原子數(shù);m為原子質量;Tcell為原子氣室溫度;kb為玻爾茲曼常量;式(4)中的c為光速;式(5)中的H為CPT信號幅值系數(shù);wset為微波源設定頻率;dw為微波源設定頻率與實際輸出頻率的差值;γ為原子旋磁比;B為外磁場強度;υ為CPT信號線寬.為了便于計算,將以上所建立的信號數(shù)學模型在峰值附近的小范圍內進行簡化,得到數(shù)學表達式如下:
(6)

其中,ω為磁場對應的譜線頻率;ω0為堿金屬原子基態(tài)兩超精細能級的半頻差,二者的頻率差dω=ω-ω0.根據(jù)該數(shù)學模型編寫Matlab程序來對原始鑒頻信號數(shù)據(jù)進行擬合,結果如圖1所示,可以看出該模型在峰值附近的數(shù)據(jù)擬合效果良好,故以下使用該簡化模型來進行峰值尋找鎖定優(yōu)化算法的設計和仿真.

圖1 采集到的系統(tǒng)鑒頻信號和數(shù)據(jù)擬合效果Fig.1 Acquired system frequency discrimination signal and data fitting result
2 峰值定位鎖定方案
磁力儀通常采用斜率法作為曲線尋峰算法.斜率法尋峰是根據(jù)CPT信號峰模型曲線的斜率變化規(guī)律來確定峰值位置的[7-9].圖2顯示的是CPT模型中選取頻率差dω為-100~100時計算得到的相應斜率值.

圖2 CPT模型中頻率差值所對應的斜率值Fig.2 The slope value of the frequency difference in the CPT model
CPT信號峰值附近小范圍的頻率差值所對應的斜率值是逐漸增大的,當頻率差值正好為0時,也就是到達峰值處時得到的斜率值等于0,且峰值左側和右側的頻率值符號相反.根據(jù)信號曲線斜率的這種特點,斜率算法峰值鎖定的實現(xiàn)步驟如下:
(1) 設定曲線上的起始點dω0和固定步長d_ω;
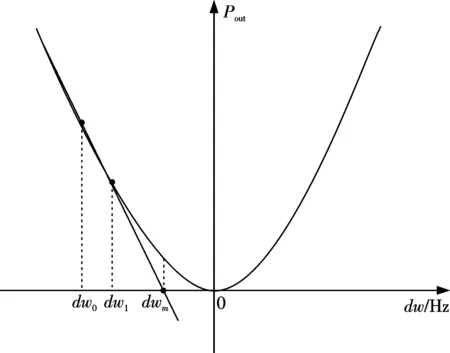
(2) 確定尋找方向,比較前后兩點的斜率值D(H0)和D(H1)大小,如果D(H0) (3) 迭代計算,按固定步長連續(xù)計算頻率差值并進行方向判斷,如果當前計算的斜率值與初始斜率值同號,則繼續(xù)正向尋找,否則反向尋找. 斜率尋峰法的優(yōu)勢在于程序結構簡單,可以根據(jù)實際情況設置合適的步長并快速定位峰值.但是,在到達目標之后如果繼續(xù)迭代計算,則會在峰值處以步長值保持振蕩,搜索步長越大則振蕩越劇烈. 本文設計了兩種新的峰值定位鎖定算法,即PI跟蹤控制算法和快速鎖定算法. 3.1PI跟蹤控制法 PI跟蹤控制法是基于PI控制器對誤差進行實時跟蹤消除的一種算法.由式(6)可知,在理想情況下,也就是當頻差為0時,CPT曲線的光功率值達到最低點.在峰值對應頻率附近進行小范圍的頻率掃描,當掃描范圍的中心頻率值與ω0的差值dw剛好為0時,從掃描曲線中可以看到該掃描中心頻率值對應著CPT曲線的極值點,并且得到的功率譜線完全對稱.當dw不為0時,掃描范圍中心與峰值頻率發(fā)生偏移,功率譜線不再對稱.例如,取掃描范圍為200 Hz,掃描范圍中心頻率偏移值為20,得到的光功率譜線如圖3所示,縱坐標表示光功率.所以根據(jù)掃描曲線的對稱性可以實現(xiàn)對頻率的調整和鎖定. (a) 中心偏移值為0 Hz時的CPT信號曲線 (b) 中心偏移值為20 Hz時的CPT信號曲線圖3 掃描范圍為200 Hz時得到的CPT信號曲線Fig 3 The CPT signal curve obtained when the scanning range is 200 Hz(a) CPT signal curve when the center offset is 0 Hz; (b) CPT signal curve when the center offset is 20 Hz PI跟蹤控制法的具體實現(xiàn)步驟如下: (1)定義算法誤差量.定義一個誤差量e來衡量掃描曲線的對稱性.把掃描頻率范圍以中心為界分為兩組頻率值,分別記為數(shù)組f1和f2,兩組頻率對應的功率值分別為數(shù)組HL和HR,對兩個功率值數(shù)組內的數(shù)據(jù)求和,分別得到ER1=sum(HL)和ER2=sum(HR).這兩組功率和值的差值可以作為尋找峰值的誤差量,表示為e=ER1-ER2.誤差量e和dw的關系為線性變化. (2)設定PI控制器參數(shù).為了使頻率偏移值保持為0,需要消除掃描模型計算得到的誤差量.本系統(tǒng)使用PI控制器來消除誤差,它的表達式為[10]: 其中,u為系統(tǒng)輸出量;e為隨時間變化的誤差量;Kp為比例系數(shù);Ki為積分系數(shù).將上式離散化成差分方程后,第k拍的輸出表示為: (3)頻率鎖定.反復迭代(1)和(2)的計算步驟,直到誤差逐漸被減小到0時,進入峰值頻率鎖定狀態(tài). 3.2 快速鎖定算法 圖4 快速鎖定算法加速確定搜尋點方法示意圖Fig.4 Search point determination acceleration method diagram of fast locking algorithm 快速鎖定算法的設計是基于原子鑒頻信號峰譜線模型,如圖4所示,以峰值點為虛擬橫坐標軸,通過兩個搜尋點dω0和dω1來推斷其所在直線與該虛擬軸的交點,從而加速尋找下一個最接近峰值的搜尋點,通過調整頻率偏移值dω=dω1-dω0來實現(xiàn)峰值定位. 快速算法具體的實現(xiàn)步驟如下. (1) 由式(7)得到其一階近似模型 當Pin-Pa-H為已知量時,取系統(tǒng)的觀測量為 (2) 給定初始值dw0,求P(dw0). (3) 給定增量.設置一個正向增量d_w,此時,有dw1=dw0+d_w,求出相應的P(dw1). (4) 確定方向.如果P(dw0)>P(dw1),表明當前頻率差值位于鎖定頻率的右側,與希望的鎖頻方向相反,則需重新選取dw1=dw0-d_w,并求取P(dw1). (5) 構造直線.由兩點(dw0,P(dw0))和(dw1,P(dw1))計算出所在直線的斜率值: (6) 求取下一個點.設在下一個頻率點,在直線方程中有P(dwm)=0,則該點的表達式為: 此點對應的觀測量為P(dwm): (7) 數(shù)據(jù)更新.取dw1=dwm,P(dw1)=P(dwm)和dw0=dw1,P(dw0)=P(dw1),代入步驟(6),進入持續(xù)迭代過程,當搜索點到達峰值位置時,鎖定在峰值點處. (8) 在Pin-Pa為未知量的情況下,仍然使用觀測量P,此時需根據(jù)觀測量不斷調整H0值.執(zhí)行步驟(2)到(7). (9) 求取下一個點.設在下一個頻率點,在直線方程中有,則該點的表達式為 此時判斷dωm和dω1的符號,如果二者同號,則此點對應的觀測量為 否則,對Pp進行更新,有 然后更新Pp和P(dωm).繼續(xù)執(zhí)行步驟(7),然后重復執(zhí)行步驟(9). 為了更直觀地進行分析,以初始值為-100,步長為3的設定情況為例來觀察算法迭代和穩(wěn)定的表現(xiàn),仿真結果如圖5所示,左圖的縱坐標表示光功率. 圖5 鎖頻過程和收斂過程Fig.5 The process of locking process and convergence 圖5展示了利用快速鎖定算法實現(xiàn)的鎖頻過程和收斂過程,左圖的縱坐標表示光功率.可以看出在程序運行能夠實現(xiàn)目標加速搜索,在快速定位峰值后穩(wěn)定狀態(tài)良好. 圖6 3種算法的仿真結果(dω=-100 Hz,d_ω=3 Hz)Fig.6 Simulation results of the three algorithms 為了觀察兩種優(yōu)化算法與傳統(tǒng)斜率算法的計算速度和收斂穩(wěn)定性,分別對3種算法編寫程序進行仿真并對結果進行比較.3種算法的頻率差值dω均設置為-100 Hz.仿真結果如圖6所示. 其中,斜率法的步長選擇為d_ω=3 Hz,仿真結果在圖中用三角形數(shù)據(jù)點表示.當?shù)嬎愕?3步時,dω=0 Hz;PI跟蹤控制法以dω=-100 Hz為掃描范圍的中心頻率值,掃描范圍為dω-100 Hz~dω+100 Hz,同時設定控制器比例放大系數(shù)kp=0.01,積分放大系數(shù)ki=0.000 01,仿真結果在圖中用圓圈數(shù)據(jù)點表示,當?shù)綌?shù)為41時,dω被調整為0,之后系統(tǒng)鎖定在峰值處;快速鎖定算法的仿真結果在圖中用星型數(shù)據(jù)點表示,搜索點在開始時快速逼近峰值點,隨后減慢速度,當?shù)降?1步時找到峰值,之后持續(xù)迭代計算并鎖定在峰值位置. 從仿真結果可以看出,斜率算法始終按照固定步長更新數(shù)據(jù),步長設置越大,峰值定位所需步數(shù)越少,但是在到達峰值處之后在dw=0附近保持振蕩,振幅等于設置的步長值,這也意味著該算法不能使用大步長搜索;PI跟蹤控制法搜索峰值所需的迭代次數(shù)最多,但是與斜率算法相比,鎖定峰值點的穩(wěn)定性更好;快速鎖定算法在進行搜索點初始決策時,能快速逼近峰值點,所用的迭代次數(shù)最少.另一方面,該算法越接近峰值點時計算步長越小,可以實現(xiàn)峰值頻率的準確定位,并保持很好的穩(wěn)定狀態(tài). 綜上,快速算法的綜合性能與其他兩種算法相比更為出色.一方面它的峰值定位速度快,在初始步長要求設置較小的情況下具有絕對的優(yōu)勢,另一方面,該算法在峰值頻率鎖定之后的穩(wěn)定性高,不受初始步長值大小的影響.根據(jù)原子干涉磁力儀系統(tǒng)鑒頻信號的控制需求,最終選用快速鎖定算法作為CPT信號曲線鎖定算法. [1] STAHLER M,KNAPPE S,AFFOLDERBACH C,etal.Picotesla magnetometry with coherent dark state[J].Europhys Lett,2007,54(3):323-328. [2] NAGEL A,GRAF L,NAUMOV A,etal.Experimental realization of coherent dark-state magnetometers[J].Europhys Lett,1998,44(1):31-36. [3] 劉國賓,孫獻平,顧思洪,等.高靈敏度原子磁力計研究進展[J].物理,2012,41(12):803-810. [4] 黃宇翔.CPT原子磁力儀的初步研究[D].杭州:浙江大學,2013. [5] 王 豐,劉 強,曾憲金.Cs原子磁力儀共振譜線寬度的研究[J].光電子·激光,2010,21(6):846-847. [6] 滿文慶,楊世琪,鐘旭濱,等.以原子譜線作參考的半導體激光器的頻率鎖定[J].激光技術,1998,22(1):9-10. [7] 鄒鵬毅,羅深榮,顧建松,等.兩型光泵磁力儀比對試驗結果及分析[J].聲學與電子工程,2008,41(2):35-45. [8] 李 芳.磁通門磁力儀的設計與研究[D].長春:吉林大學,2014. [9] 柯超凡,彭 翔,徐盛晨,等.基于虛擬儀器的光泵磁力儀測控系統(tǒng)設計[J].紅外與激光工程,2013,42(12):3316-3319. [10] 任 昊,王學鋒,楊學禮,等.輸入光功率對探測器組件帶寬的影響分析[J].導航與控制,2012,11(1):63-67. (編輯 CXM) Frequency Discrimination Optimization Algorithm Design for Atomic Interference Magnetometer ZHANGXiao-nan1,2,SUNXiao-jie2,KOUJun2,WEIZong-kang2,RENZhang1* (1.School of Automation Science and Electrical Engineering,Beihang University,Beijing 100191,China;2.Beijing Institute of Aerospace Control Instrument,Beijing 100039,China) Atomic interference magnetometer is able to calculate the value of the magnetic field strength by collecting the CPT frequency discrimination signal curve peak which corresponding to the frequency value though the light quantum sensor.The resolution and response speed of magnetometer are directly affected by the search speed,accuracy and stability of signal peak positioning and locking algorithm.Slope algorithm is widely used in magnetometer system and only suitable for small step length search with slow location speed and low stability of the locked state.In order to improve the algorithm,two kinds of optimization algorithms are designed based on the mathematical model of magnetometer signal,which are PI tracking control algorithm and fast locking algorithm.Simulation experiments are also conducted to compare the performance of the three algorithms.The results show that the fast locking algorithm is nearly not affected by the initial search step size,which also has the fastest peak position speed,and good locking stability.It is of great application potential for the performance improvement of atomic interference magnetometer system. atomic interference magnetometer; CPT frequency discrimination signal; signal peak positioning and locking; optimization algorithm 10.7612/j.issn.1000-2537.2017.01.011 2016-09-22 國家自然科學基金資助項目(11204011) * 通訊作者,E-mail:meiye100@hotmail.com U652 A 1000-2537(2017)01-0071-063 鑒頻信號算法設計

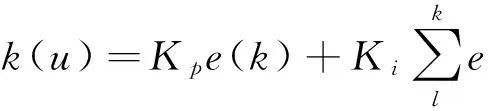


4 算法仿真結果分析


