分形圖案在電腦提花針織面料上的應用

路麗莎， 宋曉霞

(上海工程技術大學 服裝學院，上海 201620)

研究與技術

分形圖案在電腦提花針織面料上的應用

路麗莎， 宋曉霞

(上海工程技術大學 服裝學院，上海 201620)

圖案是針織面料不可或缺的藝術表現語言，針織面料的圖案可以由組織結構和色彩來表現，色彩圖案也即提花。針對目前針織面料的圖案主要是由傳統圖案構成的問題，文章根據分形圖案的不同生成原理，利用C++語言編寫了基于生成元和逃逸時間算法的分形圖案，并在電腦橫機的花型設計軟件中對生成的圖案進行二次設計，最后將設計好的花型程序導入電腦橫機中進行實際的編織。結果表明：基于生成元生成的分形圖案可以重新排列組合后應用在針織提花面料上，基于逃逸時間算法生成的分形圖案可以以局部或滿花的形式應用在提花面料上。

分形圖案；二次設計；電腦橫機；針織面料；提花面料；編織

圖案可以對面料進行修飾和點綴[1]，對于針織面料而言，圖案常用色彩圖案即提花來表現。提花就是按照花紋要求，選擇某些織針進行編織成圈而形成的帶有花紋圖案的組織，一行有幾種顏色就叫幾色提花，隨著紗線顏色數的增多，織物會越來越厚。分形圖案是一種復雜的、不規則的圖形，利用其獨特的特性，可以構造出千變萬化的藝術圖案，從而為針織面料圖案設計提供靈感。本文根據分形圖案不同的生成原理，從基于生成元和逃逸時間算法的分形圖案出發，研究其在針織提花面料中的應用。

1 分形圖案概述

分形是用來描述自然界中存在的粗糙和不規則的幾何形體，如動物的血管、起伏的山脈、漂浮的云朵等。分形是由計算機創作生成的，由于其獨特的美學特征，在物理、建筑及藝術等領域有著廣泛的應用。分形主要有以下幾個特征[2]：

自相似性：指分形在生成過程中產生出許多和自己相似的部分；不規則性：是指它的整體和局部都不能用傳統的幾何語言來描述，它既不是滿足某些條件的點的軌跡，也不是某些簡單方程的解集；精細性：分形圖案具有精細的結構、蘊涵著無窮的嵌套結構，在放大任意倍數下，也具有復雜的結構形態；多樣性：分形圖案是通過計算機結合數學理論產生的新型圖案，不受想象力、時空的限制[3]。正是由于這些特點，如果將分形圖案應用在針織面料圖案設計上，能極大地改變面料的視覺效果，給針織面料圖案設計帶來新的設計靈感。

2 電腦提花程序的設計

2.1 提花圖案的花型設計

分形圖案的不規則性和復雜性決定了其不能直接應用在針織提花面料的圖案設計中，這就需要對其進行二次設計，使之成為符合針織面料圖案設計類型。本文借助Stoll電腦橫機的花型設計軟件Stoll-M1plus，對圖案進行二次設計。電腦橫機是一種具有雙針床選針功能的針織設備針織機械，所編織物屬于緯編的一種，生產效率高、花型變化豐富，是技術含量較高的服裝設備[4]。

將計算機生成的圖片保存為bmp格式，導入花型設計軟件中。首先對其進行去色處理，由于電腦橫機中一個導紗嘴代表一種顏色的紗線，因此在設計花型時要確保每行的顏色數應相同，否則編織出的面料會厚薄不勻，但各行的顏色可以不同，一般來說，提花織物的顏色不超過四色。對分形圖案而言，由于其不規則性難以保證在設計的過程中每行的顏色數恰好都相同，這時要對其進行邊緣處理，即在顏色數少的行的邊緣增加一兩列其他顏色到所需顏色數，從而達到每行顏色數都相同的效果。其次，若是做連續圖案，則可以根據要求進行對稱、翻轉等變化。

2.2 提花圖案的程序生成

提花的花型設計好以后就可以定義提花的結構，即確定所編織物的組織結構；對同一花型，不同的組織結構有時會直接影響花型效果。單面提花由于背面存在浮線，適用于一些規則、色塊分割較小的圖案編織，而分形圖案適用于雙面提花編織。雙面提花背面有多種組織，可以根據設計要求進行選擇。提花結構定義好后，只能用定義好后的提花顏色畫圖，不能使用其他的紗線顏色和線圈作圖。若要修改提花圖案或組織類型，還需回到提花結構定義前；其次就是對程序做分離紗和封口紗，分離紗要做在織物的前兩行，而封口紗做在大身編織完的最后兩行，任何織片的結束處都要加封口紗[4-5]。最后進行紗嘴分配和導出程序，此時就生成了一個可以用于上機編織的完整的提花程序。

3 分形圖案在針織提花面料上的應用

分形圖案的生成方法有多種，本文主要研究基于生成元和逃逸時間算法生成的分形圖案及其在雙面針織提花面料中的應用。

3.1 基于生成元生成的分形圖案

基于生成元生成的分形圖案本質上是一種迭代的算法，即給定基本元素和變化規律，反復多次遞歸、迭代后生成繽紛無限的分形圖案[6]。基本元素既可以是線也可以是面。

3.1.1 以線作為生成元的分形圖案

以線作為生成元可以生成很多分形圖案，如以一條線段為基元，第一次從該線段中點折疊成夾角為90°的兩條線段，第二次分別從兩條線段的中點向相同方向折疊90°。經過多次折疊后就形成了漂亮的分形圖案，這就是著名的萊維C形曲線[6]，如圖1所示。

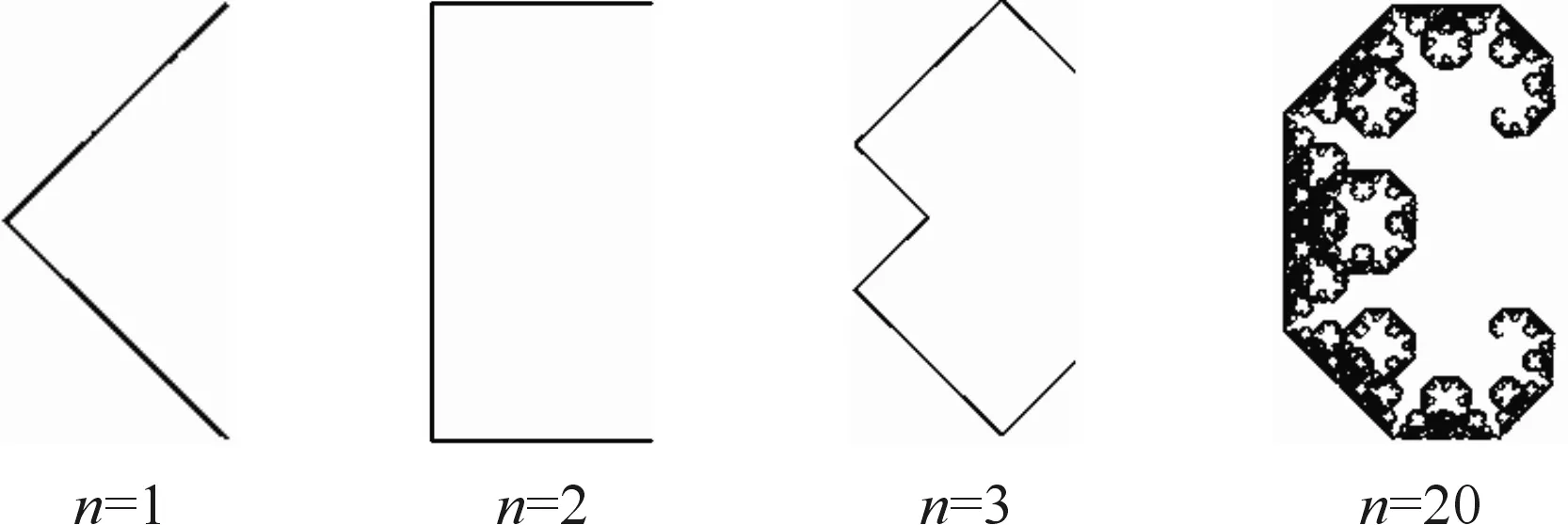
圖1 萊維C形曲線Fig.1 C shape curve of Levy

這類圖案的主要特點就是色彩簡單且隨著迭代次數的增加，內部結構會越來越精細，適宜做連續圖案，兩色便可以顯示其主要特點。以背面為芝麻點和橫條組織進行編織，芝麻點組織是每一個反面橫列由兩種色紗交替編織，背面呈現散點式的分布，屬于不完全提花組織；而橫條組織每一成圈系統所有的反面線圈對應織針都進行編織，背面呈現橫條狀，屬于完全提花組織[7]。因此，橫條組織的正反面的縱密比大于芝麻點組織，在編織的過程中圖案容易變形(易被拉長)，不宜應用于雙面提花的編織，如圖2所示。

圖2 萊維C曲線實物案例Fig.2 Object case of Levy C curve

3.1.2 以面作為生成元的分形圖案

以面作為生成元是以某一個面元素作為基元，在其基礎上根據一定的規律反復迭代后生成的一系列圖案。如以60°菱形為構成元素，從第二次開始以1︰2的大小在四個頂點處衍生小的菱形，如果某一頂點是其“父”則不衍生，依次下去就會生成一個較復雜的圖案，如圖3所示。

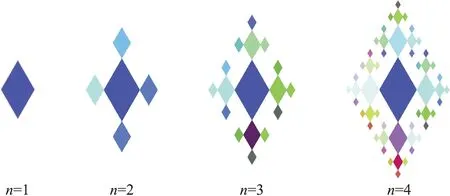
圖3 菱形格Fig.3 Diamond lattice

該圖案的最大特點是很規則，根據圖案就可以看出其迭代規律，在針織面料圖案設計中，圖案越規則，可選擇的工藝就越多。以n=4的圖形為例，選擇較復雜的翻針工藝進行編織，這是一種特殊的提花，翻針區域的色紗不再參加編織，而是由其他色紗在后針床編織反面線圈形成花型。因此，翻針的地方較薄，凹凸對比形成了立體感。另外，通過組織結構對色塊進行分割，減少了紗線數的使用，降低了織物的厚度。本文采用芝麻點翻針和橫條翻針兩種工藝編織，芝麻點翻針在翻針部位及反面呈散點分布，而橫條翻針在翻針部位及反面呈橫條狀，如圖4所示。顯然，橫條翻針圖案變形較大、卷邊性比較明顯，因此實際編織中不宜采用。

圖4 菱形格實物案例Fig.4 Object case of diamond lattice

3.2 基于逃逸時間算法生成的分形圖案在提花面料上的應用

逃逸時間算法是一種基于迭代法的畫圖法，假設f是一個變換，f的n次迭代fn為f0(x)=x，f1(x)=f(x)，fn+1(x)=f(fn(x))，n=0，1，2…。逃逸時間算法的生成原理就是在計算機中確定圖形區域并建立坐標系，將區域中像素的坐標依次代入到相應的迭代公式中，并計算該像素點的坐標在給定的迭代次數下是收斂還是發散；將區域收斂的像素用一種顏色表示，發散的像素用另一種顏色表示，在給定的迭代次數下由于每個像素點收斂的迭代次數不同，發散的迭代次數也不同，這樣分別添加不同的顏色就得到了絢麗多彩的分形圖案。逃逸時間算法下生成的圖案有經典的Mandelbrot集、Julia分形集及Newton迭代分形等，其主要特點就是色彩絢爛、結構復雜、對任一個局部放大均會出現復雜的圖案。

3.2.1 局部形式的應用

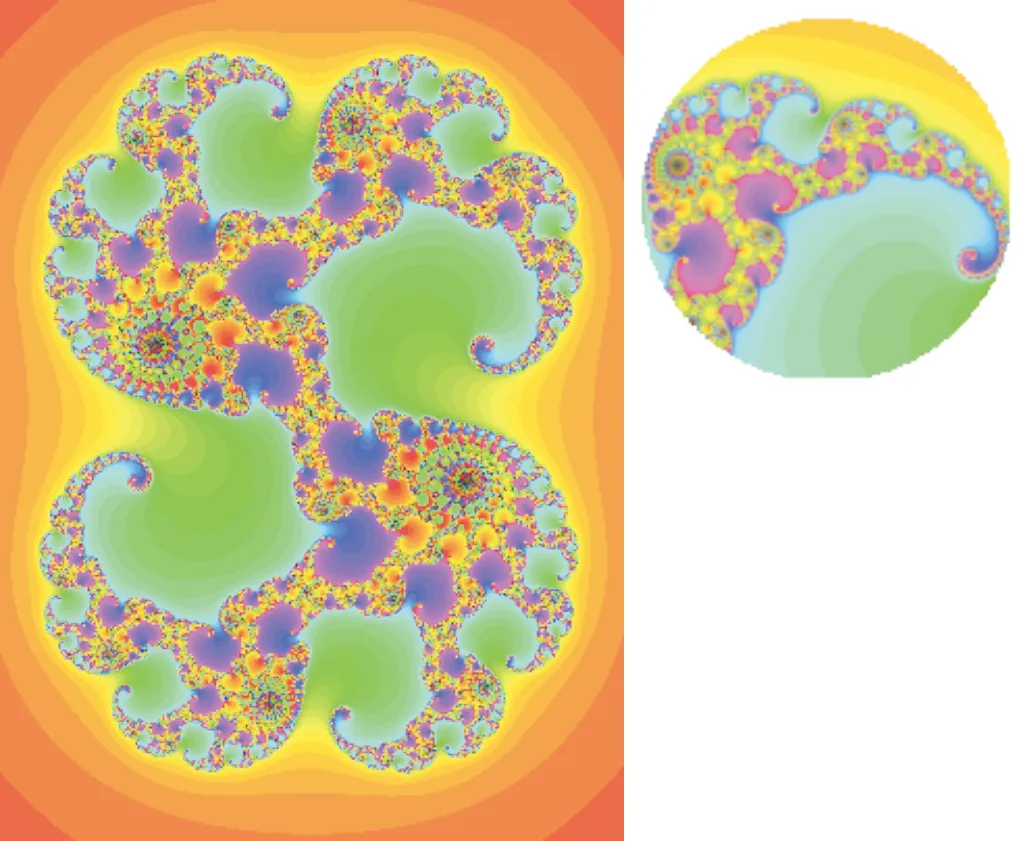
圖5 Julia分形圖案Fig.5 Julia fractal pattern

圖6 Julia集正面示意Fig.6 Front diagram of Julia set

圖7 Julia集反面示意Fig.7 Back diagram of Julia set

3.2.2 滿花形式的應用

所謂滿花形式就是將計算機生成的整個圖案應用于針織面料的圖案設計中。以Newton迭代分形為例，牛頓分形是依據牛頓迭代公式zn+1=zn-f(zn)/f′(zn)而生成的圖案[10]，f(x)可以為任意基本函數，當函數不同時，生成的圖案也不同。圖8所示的f(x)=tanx時的圖案，該圖案本身就是一種連續圖案，可以以滿花的形式應用在針織面料的圖案設計中。

圖8 Newton迭代分形圖象Fig.8 Newton iteration fractal pattern

為了更清晰地表現圖8的花型效果，設計了4種顏色的花型，如圖9所示。由于4色雙面提花織物比較厚，而抽針網絡組織能達到保持原有花型和降低厚度的雙重效果，且抽針次數越多，織物就越薄，所以選擇網絡及網絡1×2進行編織。兩種組織相比，正面效果完全一樣，網絡1×2反面花紋清晰度降低，織物的厚度減少但并不疏松，如圖10所示。因此，對于4色提花來說，抽針網絡提花可以應用，甚至可以做1×3抽針處理。從保暖的角度選擇網絡組織編織，從節約成本的角度選擇抽針網絡編織。

圖9 Newton迭代分形正面示意Fig.9 Front diagram of Newton iteration fractal

圖10 Newton迭代分形反面示意Fig.10 Back diagram of Newton iteration fractal

4 結 語

通過C++生成多種分形圖案，將生成的分形圖案運用電腦橫機花型軟件設計出針織提花程序，最后采用不同的工藝進行了編織，并比較分析了每種工藝的特點。通過將分形圖案應用在提花面料圖案設計上，不僅打破了傳統針織面料圖案設計的局限性，而且以更有新意、美感的優勢，為針織面料的圖案提供了新的設計方法和創作靈感，從而也進一步擴大了分形圖案的應用領域。

[1]于超.基于分形的藝術圖案生成方法的研究與應用[D].濟南:山東師范大學,2007:26-27.YUChao.ResearchandApplicationsoftheArtisticGraphicsGenerationMethodBasedonFractalTheory[D].Ji’nan:ShandongNormalUniversity,2007:26-27.

[2]蔡燕燕.分形幾何在服裝圖案設計中的研究與應用[D].上海:上海工程技術大學,2011:4-7.CAIYanyan.ResearchandApplicationofFractalGeometryinFashionDesign[D].Shanghai:ShanghaiUniversityofEngineeringScience,2011:4-7.

[3]徐向紅.分形理論在服飾圖案設計中的應用基礎研究[D].長春:吉林大學,2009:17-34.XUXianghong.AppliedBasicResearchofFractalTheoryinClothingPatternDesign[D].Changchun:JilinUniversity,2009:17-34.

[4]姜曉慧,王智.電腦橫機花型設計實用手冊[M].北京:中國紡織出版社,2014:65-68.JIANGXiaohui,WANGZhi.InstructionManualofComputerizedFlatKnittingMachinePattern[M].Beijing:ChinaTextile&ApparelPress,2014:65-68.

[5]朱文俊,鄭建林.電腦橫機編織技術[M].北京:中國紡織出版社,2011:265-275.ZHUWenjun,ZHENGJianlin.ComputerFlatKnittingMachineKnittingTechnology[M].Beijing:ChinaTextile&ApparelPress,2011:265-275.

[6]吳運兵.分形理論在計算機圖形設計中的研究與應用[D].西安:西安科技大學,2004:21-32.WUYunbing.ApplicationsofFractalTheoryinComputerGraphicsDesign[D].Xi’an:Xi’anUniversityofScienceandTechnology,2004:21-32.

[7]裘玉英,陳天里.電腦提花針織物組織結構設計及性能分析[J].絲綢,2013,50(2):35-38.QIUYuying,CHENTianli.Structuredesignandperformanceanalysisofcomputerjacquardfabricorganization[J].JournalofSilk,2013,50(2):35-38.

[8]萬愛蘭,繆旭紅,叢洪蓮,等.緯編技術發展現狀及提花產品進展[J].紡織導報,2015(7):35-39.WANAilan,MIUXuhong,CONGHonglian,etal.Developmentstatusofweft-knittingtechnologyandrelatedjacquardproducts[J].ChinaTextileLeader,2015(7):35-39.

[9]唐穎,房寬峻.分形在數字噴墨印花圖案設計中的應用[J].紡織導報,2009(6):112-115.TANGYing,FANGKuanjun.Applicationoffractalinthepatterndesignofdigitalink-jetprinting[J].ChinaTextileLeader,2009(6):112-115.

[10]丁玲聰,張聿.應用廣義牛頓迭代圖形的絲巾紋樣設計方法[J].絲綢,2015,52(11):47-51.DINGLincong,ZHANGYu.DesignmethodofscarfpatternswithGeneralizedNewtoniterationgraphics[J].JournalofSilk,2015,52(11):47-51.

Application of fractal pattern in computer jacquard knitted fabric

LU Lisha, SONG Xiaoxia

(Fashion College, Shanghai University of Engineering Science, Shanghai 201620, China)

Pattern is the indispensable artistic language of knitted fabric. The pattern of knitted fabric can be expressed by structure and color. Color pattern is also jacquard. Since current knitted fabric patterns are mainly composed by traditional patterns, the paper applies C++ language to program fractal pattern based on generating element and escaping time algorithm according to the different generating principles and then redesigns the pictures in the pattern design software of computerized flat knitting machine. Finally, the designed pattern program is inputted to computerized flat knitting machine for practical weaving. The result shows that the fractal pattern generated on the basis of generating element can be rearranged and recombined, and then applied in knitted jacquard fabric. The fractal pattern generated on the basis of escaping time algorithm can be applied in jacquard fabric in the form of partial or full followers.

fractal pattern; secondary design; computerized flat knitting machine; knitted fabrics; jacquard fabric; knitting

10.3969/j.issn.1001-7003.2017.02.006

2016-05-12;

2016-12-11

路麗莎(1989-)，女，碩士研究生，研究方向為針織服裝的研究。通信作者：宋曉霞，教授，songxiaoxiavivi an.@126.com。

TS181.8

A

1001-7003(2017)02-0025-05 引用頁碼: 021106