理論力學(xué)教學(xué)中平面力系平衡的深入探討

鄭州大學(xué)力學(xué)與工程科學(xué)學(xué)院 何尚文

鄭州工商學(xué)院建筑工程學(xué)院 唐華瑞 苗同臣

理論力學(xué)教學(xué)中平面力系平衡的深入探討

鄭州大學(xué)力學(xué)與工程科學(xué)學(xué)院 何尚文

鄭州工商學(xué)院建筑工程學(xué)院 唐華瑞 苗同臣

總結(jié)平面力系平衡教學(xué)中的相關(guān)經(jīng)驗，結(jié)合具體實例深入分析平面匯交力系、平面平行力系、平面力偶系及平面任意力系平衡的聯(lián)系與區(qū)別，總結(jié)出解決平面力系平衡問題的一般規(guī)律，揭示平面力系平衡的本質(zhì)，使學(xué)生為后續(xù)知識學(xué)習(xí)奠定堅實的基礎(chǔ)。

理論力學(xué)教學(xué)；平面力系；平衡方程；平衡

在理論力學(xué)教學(xué)中，力系平衡問題是非常重要的內(nèi)容，它是后續(xù)相關(guān)力學(xué)課程學(xué)習(xí)的關(guān)鍵基礎(chǔ)。使學(xué)生熟練掌握應(yīng)用力系平衡方程解決各類工程問題的一般規(guī)律，深入透徹地理解力系平衡的本質(zhì)，理清力系平衡涉及的關(guān)鍵觀念，建立完整的知識體系是我們教學(xué)的核心目標(biāo)。

1 平面力系的平衡方程

平面力系平衡問題是平面力系簡化的深化和延續(xù)。根據(jù)平面力系簡化的結(jié)論，力系平衡的充要條件為主矢和主矩同時為0。要區(qū)分力系平衡和系統(tǒng)平衡兩個概念，系統(tǒng)平衡必有所受力系平衡，反之不一定成立。

平面任意力系的平衡方程，主矢、主矩同時為0，表達式如下（n為力系中力的個數(shù)）[1][2]：

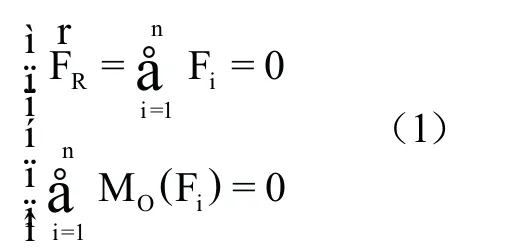
方程第一式為矢量方程；由于平面力系的矩可理解為標(biāo)量，第二式為標(biāo)量方程。

1.1 平面任意力系的獨立平衡方程

對于平面任意力系，是平面上任意一點，將矢量方程描述為代數(shù)方程，則（1）式可寫為式（2）[3]，即為平面任意力系的平衡方程，顯然這3個代數(shù)方程是相互獨立的。

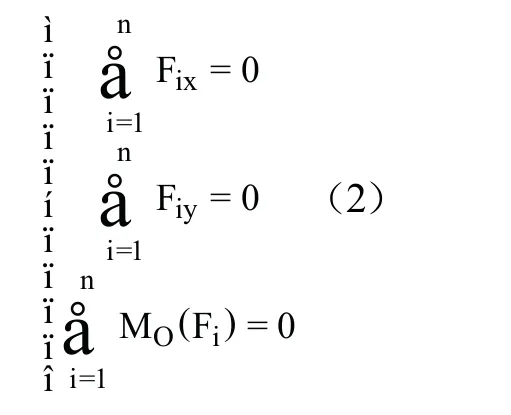
1.2 平面匯交力系的獨立平衡方程

對于特殊的平面匯交力系，是平面上任意一點，是力系匯交點。其合力為通過匯交點的主矢，若此主矢為0，則對任意一點主矩自然為0，即平衡方程（2）中的第三式由前兩式線性組合，同理第一式或第二式是也可由其他兩式線性組合，相應(yīng)平衡方程可寫為式（3）或（4）[4]。

式（3）、（4）為平面匯交力系平衡方程的幾種形式，兩個獨立方程，與式（2）比較可知平面匯交力系與平面任意力系平衡方程的區(qū)別與聯(lián)系。

1.3 平面平行力系的獨立平衡方程

對于特殊的平面平行力系，O是平面上任意一點。則平衡方程（2）中的前兩式線性相關(guān)，平面平行力系的平衡方程可表達為式（5）[4]。

式（5）為平面平行力系2個獨立的平衡方程。與式（4）比較可知，平面匯交力系與平面平行力系具有相同形式的平衡方程，可理解為平面平行力系是匯交點為無窮遠點的特殊平面匯交力系。

1.4 平面力偶系的獨立平衡方程

對于特殊的平面力偶系，其主矢自然為零，O是平面上任意一點。平衡方程（2）中前兩式自動為零，則平衡方程形式轉(zhuǎn)化為式（6）[5]，只有一個獨立的平衡方程。

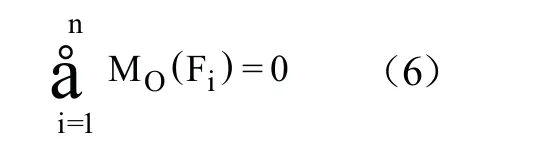
2 平面力系平衡方程典型例題分析

例：梯子上端B靠在鉛垂墻壁上，下端A擱置在水平地面上，與墻壁之間為光滑約束，而與地面之間為非光滑約束。梯子與地面間的摩擦因數(shù)為fs，梯子重力為W，長為l。設(shè)梯子在傾角1位置保持平衡，求A、B處約束力FNA、和摩擦力FA。

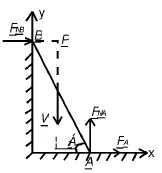
圖1

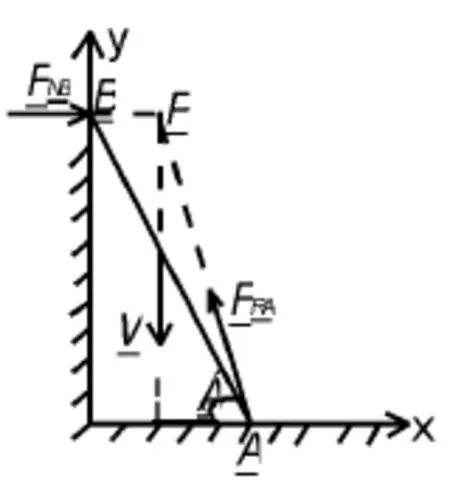
圖2

解一：按平面任意力系的平衡方程求解，3個平衡方程求解3個未知量。

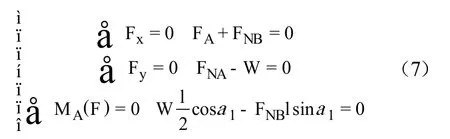
解二：按平面力偶系平衡方程求解，認(rèn)為圖中兩個水平力與兩個豎直力分別組成一個力偶，一個平衡方程，補充兩個組成力偶的條件。

解三：如圖2按平面匯交力系平衡方程求解。FNB與W匯交于P點，則全約束力必通過點，補充一個幾何條件。設(shè)FRA與X軸負(fù)方向夾角為，則

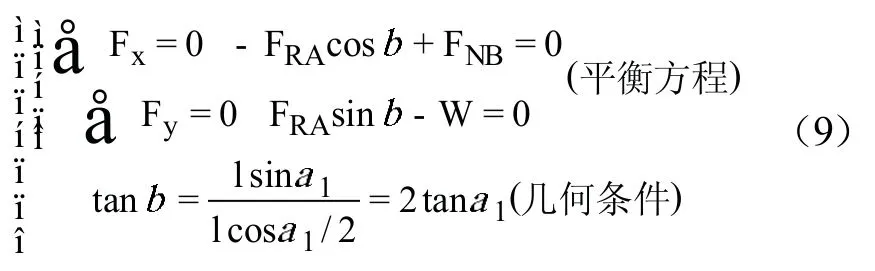
比較解一、解二與解三可知：式（8）中組成力偶的條件與式（7）中前兩個平衡方程等價；式（9）與式（7）的3個方程（條件）完全等價，即式（7）、（8）、（9）完全等價，3種解法完全等價。

綜上，平衡前提下平面力系可以看成平面任意力系、平面匯交力系、平面力偶系或平面平行力系；對一個研究對象其解決平衡問題的獨立方程（條件）總是可以列出3個，要么是3個平衡方程，要么是1個或2個平衡方程加上其他方程（條件）；解決問題的方法取決于將該平面力系看成那種力系，n個構(gòu)件組成的平衡系統(tǒng)總可列3n個獨立方程（條件）。該結(jié)論可推廣至空間力系平衡問題，也是文獻[6][7]分析的進一步深化。

3 平面力系平衡的本質(zhì)

理解力系平衡是從二力平衡的概念出發(fā)的，到三力匯交平衡，再到任意力組成的復(fù)雜力系的平衡。那么對于一個系統(tǒng)，其所受力系為任意的平面力系，其平衡的本質(zhì)是什么呢？圖1：看作平面任意力系，F(xiàn)NB與W匯交于p點，則其可合成為一個過p點的力FP，F(xiàn)A與FNA合成為通過A點的FRA，則該力系平衡可理解為FP與FRA二力平衡；若看作平面力偶系，與前分析相同，該平面任意力系依然可理解為FP與FRA二力平衡；圖2：看作平面匯交力系，F(xiàn)NB與P匯交于點合成為力FP，則該力系平衡也可理解為FP與FRA二力平衡。

綜上：任意一個平面力系的平衡均可理解為二力平衡，即從平衡的平面力系中任意選擇一個力，則平衡一定可以看作力系中其余力的合力與該力的二力平衡；或者從平衡的平面力系中任意選擇幾個力，則平衡一定可以看作這幾個力的合力與力系中其余力的合力組成的二力平衡。該結(jié)論可推至任意的空間力系平衡，將平衡的本質(zhì)歸結(jié)為二力平衡對于學(xué)生理解平衡問題有重要意義。

[1]哈爾濱工業(yè)大學(xué)理論力學(xué)教研室.理論力學(xué)（第7版）.北京:高等教育出版社,2009.

[2]洪嘉振,劉鑄永,楊長俊.理論力學(xué)（第四版）.北京:高等教育出版社,2015.

[3]謝傳鋒,王琪.理論力學(xué).北京:高等教育出版社,2009. [4]周又和.理論力學(xué).北京:高等教育出版社,2015.

[5]劉延柱,楊海興,朱本華.理論力學(xué)（第二版）.北京:高等教育出版社,2000.

[6]汪思偉.平面靜力方程的獨立性問題.重慶交通學(xué)院學(xué)報,1982，3（3）：106-112.

[7]李豐良.平面任意力系平衡方程的獨立性.力學(xué)與實踐,2001，3（23）：62-64.

0312.2

A

2017-01-05）

國家自然科學(xué)基金(51405452)、河南省高等學(xué)校重點科研項目(15A130002)資助.