數學課堂的“扎實味”

湯琪

新課程理念下的數學課堂教學展現了新的教法、新的學習方式、新的教學手段，讓學生成為學習的主人.但是不容忽視的是，當下很多“熱鬧”“新理念”的課堂背后所體現出的是教師對于教學方法、手段過度使用，對于教學理念的過度解讀，整堂課下來導致很多學生知其然而不知所以然，基礎知識和基本技能都沒有真正掌握，更談不上基本數學思想的發展.因此筆者以為“扎實”是數學教學必須要有的味道，扎實的數學教學是高效的數學課堂，是回歸探究數學本質的課堂教學.

一、扎實味是始于教學目標的教學設計

數學課堂的扎實味在于數學教學是否能充分考慮考慮數學本身的特點，學生是否扎實有效地掌握基礎知識和基本技能，引發數學思考、情感態度得到扎實有效的發展，即數學教學的扎實味應是始于教學目標的教學設計.因此數學課堂教學應圍繞教學目標，選擇合適的教學素材和情境，合理的多媒體方式及教學手段、方法，設計教學過程，使一切教學活動都始于教學目標的實現去展開教學.例如，“解決問題的策略——轉化”第一課時的教學目標如下：①讓學生初步學會用轉化的策略分析問題，靈活確定解決問題的思路，并能根據問題的特點確定具體的轉化方法，從而有效地解決問題.②讓學生通過回顧曾經運用轉化策略解決問題的過程，從策略的角度進一步體會知識間的聯系，感受轉化的應用價值.③讓學生進一步積累運用轉化的策略解決問題的經驗，增強解決問題的策略意識，主動克服解決問題過程中遇到的困難，獲得成功的體驗.

根據以上所確立的教學目標，在設計教學過程時，應該著重把握以下幾個核心問題：什么是轉化的策略？怎么轉化？為什么要轉化？即轉化的方法、轉化策略運用、轉化的應用價值.始于這樣的教學目標，“轉化的策略”一課教學設計構思：

1.自主探究新知，初步理解圖形中的“轉化”策略.設計兩個比較，圖形周長的比較和面積的比較.在圖形比較中，產生轉化圖形的需求，初步理解掌握轉化的策略，知道轉化可以把不規則轉化為規則，體驗借助于平移和旋轉進行轉化，在變與不變中，把不規則圖形轉化為規則圖形，進而復雜的問題轉化為簡單的問題，這就是——轉化.

2.回顧舊知，感受轉化的價值.首先通過回顧多邊形面積推導過程感受轉化的價值，同時再次發現實現轉化的策略，還可以借助像剪、拼等其他辦法進行轉化，所以在進行轉化時，一定根據實際情況靈活選擇相應的手段.其次回顧數與計算中的轉化運用，讓學生感受轉化并不僅僅是圖形與圖形的轉化，還有即將學習的數與數的轉化，數與形之間的轉化.

3.利用策略去解決的各種實際問題……整個教學設計完全始于教學目標，始終圍繞“什么是轉化的策略？怎么轉化？為什么要轉化？”三個教學目標中的核心問題進行設計并開展教學.在問題的解決中，使學生理解和掌握基本的數學知識與技能、數學思想和方法，獲得基本的數學活動經驗，而且各個目標之間在功能上形成了一種相互促進的關系，而這正是實施新課程的目的所在.

二、問題情境中的扎實味

問題情境在數學課堂教學中的作用已然是無可替代的.問題情境的創設是為有效達成教學目標服務的，是為學生提供廣闊的思維平臺，在生活化問題解決過程中幫助學生構建新知、體驗感受數學的應用價值，真正讓學生成為數學的主人.這就是扎實味的問題情境.例如，學生在學習“小數的意義和讀寫”一課之前，多數學生對于小數的意義的理解還是膚淺的，可能并沒有真正由感性認識上升到理性上的理解.實際教學中，教師在教學中對教材進行重組改編，把復習一位數的情境與例題結合起來，通過創設學校定制課桌椅的問題情境，對課桌的長寬的測量，發現用米作單位課桌的長寬不足1米，需要用一位小數表示，在復習鞏固基礎上進一步加深學生對一位小數意義的理解；第二層次椅面的長寬的測量發現不是整分米數，把米尺平均分成10份無法精確測量出椅面的長寬，由此引出把1米平均分成100份，即兩位小數的需求，從而探究兩位小數的意義；第三層次，引導學生發現課桌椅面厚度是9毫米、23毫米平均分成100份的米尺無法精確測量，引出需把1米平均分成1 000份，這時用米作單位，需要用幾位小數表示呢？通過學生探究、構建三位小數的意義.只有真正讓問題情境的扎實味體現出來，才能通過情境來調動學生思維的參與，促使學生真正進入獨立探究，構建新知的狀態中，達到掌握知識和技能、發展數學思想和方法，獲得基本的數學活動經驗，使學生在學習中真正成為課堂的主體，體現出數學課堂的扎實味.

三、練習的扎實味

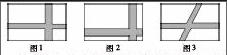
數學課堂的練習要有扎實味，不是提倡機械重復、生硬呆板的題海訓練，而是給學生提供一個廣闊的思維空間，使學生既能夠通過適量練習有效達成雙基，也能夠通過練習發展學生的數學思維，體驗數學知識的應用價值.例如，在“解決問題策略——轉化”一課練習環節中，教材僅僅安排了探究圖1草地面積問題.事實上僅此題的練習效果也僅僅是運用轉化的策略發現草坪的面積就是去掉小路后拼成的長方形的面積，無法真正有效地讓學生感受轉化策略的價值，也無法真正拓展學生的數學思維.

實際教學中，第一層次練習引導學生比較這三幅圖中草坪面積，使學生明確運用轉化的策略，在運用策略過程中感受策略的價值，增強策略的意識.第二層次學生自主設計方案，要求和圖中的草坪面積和小路面積相等.由此給予了學生廣闊思維空間，學生發現只要小路寬度相等，不管在什么位置，草坪面積和小路面積都相等，從而體會轉化策略的本質.扎實味的練習更多的是在讓學生獲得雙基訓練基礎上，提供開闊思維的平臺，拓展學生思維，探尋數學知識的本質及練習，使學生的數學思維和方法得到訓練.

只有真正為學生提供廣闊的思維空間，引導學生構建新知、感受數學知識運用價值，發展數學的思維和方法，使學生的學習由“被動”變為“主動”，才是真正的有著數學味、扎實味的數學課堂.