間歇過程最優迭代學習控制的發展:從基于模型到數據驅動

池榮虎 侯忠生 黃彪

化學工業是世界經濟的重要部分,可將原材料轉換成70000多種當今高質量生活不可缺少的產品[1].化學工業過程包括連續操作和非連續操作.間歇過程是非連續操作的主要方式,適于小批量生產,更具有靈活性,成為精細化產品生產的理想方式[2],已廣泛用于城市污水處理[3]、紙漿造紙[4]、半導體工業[5]、醫藥生物發酵[6]、工業結晶過程[7]等.

間歇過程的控制與連續過程不同,主要在于兩方面:1)間歇過程沒有穩態操作點,設定點和控制信號是時變的;2)間歇過程是在有限時間上重復運行的,具有兩個相互獨立的變量,運行時間t和運行次數k.獨立變量k提供了實現控制目標的額外自由度.因此,間歇過程的控制策略可分為兩大類:一類是在線控制策略,例如基于PID或更復雜控制技術的反饋控制[8],以及用于產品終端控制的模型預測控制(Model prediction control,MPC)方法[9].另外一類是基于重復學習的迭代學習控制[10?12]和用于產品終端輸出控制Run-to-run控制[13?15].近年來,也有文獻[16?18]采用終端迭代學習控制策略處理間歇過程產品終端質量控制問題.

迭代學習控制(Iterative learning control,ILC)最早是由Arimoto等[19]提出的,針對重復運行的被控系統,不斷重復一個相同軌跡的控制嘗試,利用前一次或前幾次操作時測得的誤差信息和控制輸入信息修正當前操作的控制輸入,使該重復任務在該次操作中做得更好,最終實現在整個時間區間上,系統的輸出完全跟蹤上期望軌跡.近年來,間歇過程的迭代學習控制逐漸成為研究熱點.Lee等[20?21]提出了基于反饋的學習控制策略,并考慮了濾波技術來增強對建模誤差和隨機擾動的魯棒性.Liu等[22]基于間歇過程的2D模型提出了一種魯棒閉環ILC方法,在線性矩陣不等式約束下建立了保證閉環ILC系統魯棒穩定性的充分條件.文獻[23?25]提出了基于設定點迭代學習的PID控制策略,得到了魯棒漸近收斂的充分條件.文獻[26]提出了一種PD-型迭代學習控制用于生物反應器,并采用了模糊方法計算控制增益.文獻[27?30]為間歇過程設計了多種魯棒ILC控制策略.時滯問題廣泛存在于工業間歇過程中,對許多控制系統的穩定性和控制性能都造成了破壞.因此,時滯系統的ILC設計問題引起了學者的關注[31?32],如文獻[31]提出了輸入時滯的時變不確定間歇過程的魯棒迭代學習控制方法,給出了2D狀態預測器對系統狀態進行預測,以此補償輸入延遲的影響.

需要說明的是,傳統的PID-型迭代學習控制方法的優點在于需要模型信息少,結構簡單,易于實現.然而,問題在于學習增益固定不變,在適應被控系統變化和外界擾動等不確定性方面的能力相對較弱,并且在實際應用中很難選取合適的學習增益.盡管[26]討論了利用模糊規則計算學習增益的方法,但模糊規則的選擇本身就是非常困難的.

迭代學習控制很容易與其他控制方法相結合,產生新的控制策略.例如,文獻[33]在迭代學習控制任務中引入了自適應機制,提出了基于能量函數設計的連續時間系統的自適應迭代學習控制方法.進一步,文獻[34?35]將關鍵引理技術推廣到迭代域中,提出了離散時間系統的自適應迭代學習控制策略以及時變參數的迭代辨識方法.迄今,自適應ILC及自適應迭代學習辨識方面的研究已獲得很多成功的應用[36?40].限于篇幅,關于這方面的內容和結果不再一一列舉.

另一方面,文獻[41]基于Lifted技術將被控對象用超向量形式重新描述為關于迭代次數的演變形式,從而可很容易地將最優技術引入到迭代學習控制任務,提出了模最優的迭代學習控制方法.如文獻[42]所指出的,在基于二次性能指標的迭代學習控制的研究框架下,各種實際問題,例如受限約束、干擾、量測噪聲及模型誤差等,都可很容易地作為最優問題的約束條件而被嚴謹地綜合到最優ILC控制器的設計中.另外,最優迭代學習控制具有沿迭代方向的嚴格單調收斂性,是實際工程應用中最為期望的性質之一.

因此,最優迭代學習控制方法在間歇過程為主的重復運行系統中得到了廣泛應用,其理論研究經歷了從線性到非線性,從基于模型到數據驅動的發展歷程.Moore等[43]提出了一種L1最優魯棒迭代學習控制方法,處理系統的未知有界擾動問題.Xu等[44]以時間最優和魯棒性為綜合目標,提出了一種新的魯棒ILC最優設計和收斂性分析方法,給出了收斂速度的理論分析和評估,研究了系統動態如何影響學習性能的問題.文獻[45]基于線性時變攝動模型,提出了一種分層ILC方法,用于晶體冷卻過程.當控制變量不可測時,文獻[46]提出了一種基于遞歸貝葉斯估計的最優迭代學習控制方法,并將其推廣到基于線性化的非線性離散時間系統中.針對系統約束問題,文獻[47]提出了基于二次性能指標的魯棒ILC的線性矩陣不等式方法.文獻[48]提出了Pareto迭代學習控制方法,討論多性能目標的優化問題.文獻[49]提出了加速預測最優ILC收斂的方法,給出了兩個加速算法和相應的收斂性分析.結果表明該方法可提高預測最優ILC的控制性能.文獻[50]基于內模原理,提出了最優ILC控制增益的多目標設計方法.Liu等[51]提出了一種改進的基于最優化指標的迭代學習算法,保證控制信號收斂于系統的線性二次型最優控制解.

由于間歇過程的非線性和有限性特點,很多學者嘗試結合模型預測控制方法.文獻[52?57]提出了一些基于模型預測控制的迭代學習控制方法.文獻[58]結合二次型ILC和間歇模型預測控制技術,提出了一種兩階段算法.

隨著社會經濟的不斷發展,現在工業過程變得越來越復雜,規模越來越大,一些所謂的“硬非線性特性”包括摩擦非線性、飽和非線性、死區非線性、間隙非線性、時滯非線性等,大量存在于實際控制工程中,經常會引起控制系統不期望的性態[59].因此,非線性系統的最優迭代學習控制引起了人們的重視.

非線性系統的最優ILC的設計,首先要對原非線性被控系統進行線性化,得到線性估計模型,在此基礎上進行最優ILC的設計和分析.因此,線性化方法是處理非線性控制系統的關鍵.

在常用的線性化方法中,泰勒展開[60]和分段線性化[61]忽略了高階項,至多是對原非線性系統的近似;反饋線性化[62]需要精確已知被控系統的非線性結構和參數;正交函數線性化[63]依賴于正交基空間的選取,所得到的線性化模型含有大量不確定參數.因此,盡管文獻[64?66]基于非線性系統的線性名義近似模型,討論了非線性系統的最優迭代學習控制,但所設計的控制器在實際應用中會由于模型失配和系統復雜等問題而遇到困難.

神經網絡和模糊規則在近年來的非線性控制系統的研究中非常流行.文獻[67]提出了非線性系統的動態模糊推理邊界線性化方法.文獻[68]提出了基于遞歸神經網絡模型的批ILC策略,用神經網絡模擬間歇過程.文獻[69]研究了滾筒鍋爐汽輪機的非線性模糊模型預測ILC.需要說明的是,在被控系統未知的情況下,如何選擇合適的神經網絡模型和模糊隸屬度函數一直是實際工程應用中的難題.

本質上,上述線性化方法是基于模型的[60?69],顯然對應的最優ILC控制器的設計和分析也是基于模型的.所依賴的模型越精確就使得模型本身越復雜,依此所設計的控制器也會更加復雜,從而會使閉環系統的魯棒性和可靠性降低,使控制系統的實現及應用變得更加困難.并且,控制性能很大程度上依賴于被控系統線性模型的精確程度.如果存在較大模型失配和建模誤差,沿迭代軸的單調收斂性將不再保證.另外,為了減小計算負擔,大多數最優ILC的學習增益是離線計算的,一旦確定后在后續的迭代過程中將保持不變,從而對被控系統的變化和外界擾動的魯棒性相對較差.

另一方面,工業過程中每時每刻都產生并儲存了大量的數據,蘊含了關于過程運行和設備狀態的全部有用信息.因此,在無法獲得過程精確模型的情況下,如何利用這些離線或在線的過程數據直接進行控制器設計,提出基于數據驅動的控制方法,具有重要的理論和實際意義[70?75].數據驅動控制[71]指的是控制器的設計和分析中并不顯含或隱含地利用被控對象的任何模型信息,如系統矩陣、結構、狀態等,而是僅利用系統過程產生的I/O數據.數據驅動控制的目標是在精確數學模型或系統不確定性描述不可獲取情況下,充分利用系統的運行數據進行基于數據的控制系統的設計.它與基于模型的控制理論一起成為完整的控制理論不可缺少的兩個部分.關于數據驅動控制理論與基于模型的控制理論之間的辯證關系詳見文獻[70?73].

數據驅動的最優ILC方法的設計和分析的前提也是線性化.與傳統的線性化方法[60?69]不同的是,文獻[76?78]針對重復運行的非線性生產過程,提出了一種新的迭代動態線性化方法(Iterative dynamic linearization,IDL),這是一種沿迭代批次在有限時間區間上逐點展開的批量線性化方法,建立了原非線性系統完全等價的迭代線性化模型.其優點在于:1)該線性化方法是數據驅動的,是針對未知的非線性系統提出的,不需要原非線性系統的任何模型信息;2)所得到的線性化形式結構簡單、參數少,只有原非線性系統的復合函數關于控制輸入信號的偏導數需要根據系統的I/O數據進行迭代估計.因此,文獻[76?78]所提出的迭代動態線性化方法是數據驅動的、面向控制器設計的,可直接借鑒線性系統的工具和方法進行控制器的設計和分析.

隨后,文獻[76?78]借鑒線性系統的最優迭代學習控制理論的已有成果,基于上述迭代動態線性化模型,分別提出了數據驅動的最優迭代學習控制(Data-driven optimal ILC,DDOILC)、數據驅動的最優點到點迭代學習控制(Data-driven optimal point-to-point ILC,DDOPTPILC)和數據驅動的最優終端迭代學習控制(Data-driven optimal terminal ILC,DDOTILC)方法.這些方法的設計和分析直接面向未知的非線性系統,利用系統運行所得到的I/O數據,而不需要被控系統的任何建模過程.

需要說明的是,數據驅動的控制方法并不排斥基于模型的控制方法;相反,二者是相輔相成、優勢互補的關系.如文獻[70?73]所述,現實世界中的實際系統按照對象模型的可獲取性可分為:1)機理模型或辨識模型可精確獲取;2)機理模型或辨識模型可獲取但不精確,含有有限程度的不確定性;3)機理模型或辨識模型可獲取,但非常復雜、階數高、非線性強、時變性強;4)機理模型或辨識模型很難建立,或不可獲取.在上述四類被控對象中,已有的基于模型的控制方法只能很好地處理1)和部分2)等的實際對象,另一大半的被控對象則需要采用數據驅動的控制策略.換言之,數據驅動的控制方法可以處理上述所有四類被控對象,但是對于機理清楚的被控過程,基于模型的控制方法會更加可靠并具有更好的控制性能;對難以建立精確數學模型或模型較為復雜的被控過程,數據驅動的控制方法則會更有優勢.因此,如何將基于模型的控制方法和數據驅動的控制方法進行有機融合和模塊化設計是一個非常重要的研究課題.數據驅動控制方法與基于模型控制方法之間的互補型控制系統設計的部分研究成果可參見文獻[79?82].

本文主要以間歇過程作為重復運行系統的控制背景,引出迭代學習控制理論和方法,對其最優迭代學習控制的研究分支的提出和發展歷程進行較為詳細的綜述和分析.目的在于分析和借鑒基于模型的最優ILC方法的現有成果,包括系統的設計和分析工具,嘗試在迭代動態線性化的前提下,提出更多適合實際生產需求的數據驅動的最優ILC方法,解決越來越復雜的間歇過程的控制中遇到的建模困難、魯棒性差等根本難題.在數據驅動的廣義最優ILC的綜述中,主要以迭代動態線性化為主線,分別回顧和分析了完整軌跡跟蹤的最優ILC方法、多中間點跟蹤的最優點對點ILC方法以及單個終點跟蹤的最優終端ILC方法.論文同時回顧了其他數據驅動的學習控制的最新進展,提出了需要進一步研究的問題前景和方向.

本文結構安排如下:第1節是基于模型的最優ILC的回顧,目的在于明確最優ILC的概念、定義和設計過程,并分析和研究最優ILC的最新進展.第2節主要回顧了非線性重復運行系統的迭代動態線性化方法,作為后面數據驅動最優ILC設計的依據和基礎.詳細說明和分析了迭代動態線性化方法的特點和用途.第3節是數據驅動廣義最優ILC的設計和分析的回顧,包括完整軌跡跟蹤、多點跟蹤和單個終點跟蹤等三種不同的控制任務,分析了數據驅動廣義最優ILC的最新發展.第4節是結論和展望,分析了數據驅動的最優ILC的發展方向,提出了一些開放的具有挑戰性的研究問題.

1 基于模型的最優迭代學習控制

為了保證實際應用中的控制精度和可靠性,最優迭代學習控制受到越來越多的關注.最早Togai等[83]、Tao等[84]、Gorinevsky等[85]分別提出了利用梯度法、牛頓拉爾遜法和高斯法等最優方法尋找最優學習控制律.Amann等[41]首先基于范數優化原理對迭代學習控制進行了研究.利用超向量技術,對如下有限時間區間上重復運行的線性離散時間系統進行了重新描述.

簡單起見,狀態空間矩陣A,B,C假設為時不變.通過定義如下兩個超向量:

將空間方程寫成如下形式:

Amann等[41]提出了如下目標函數:

其中加入了輸入變化的懲罰項,使算法沿批次軸具有積分行為.在無其他約束和確定條件下,Amann等得出了非因果的輸入更新律

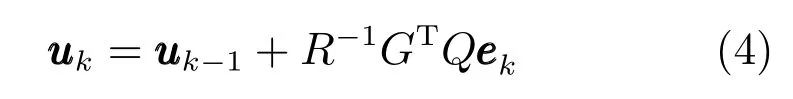
1996年,Lee等[86]根據有限時間上二次最優跟蹤問題的求解思想,將上述非因果控制律(4)改寫為如下因果形式:

Barton等[87]將基于范數優化的迭代學習控制方法用于多軸機器人,提高了運動軌跡的跟蹤性能和魯棒性.van de Wijdeven等[88]提出了基于線性二次型的最優迭代學習控制在有限時間內的魯棒單調收斂分析方法.Chu等[49]利用逐次投影方法提高了非最小相位系統的范數優化迭代學習控制算法的跟蹤性能和收斂速度.文獻[89]證明了上述二次型迭代學習控制可作為輸出反饋來實現,以增強系統的魯棒性.根據這一思想,文獻[89?90]提出了模型預測控制(MPC)與迭代學習控制的組合,成為間歇過程研究中的主要方向之一,吸引了很多學者的關注[52?58,91].

當間歇過程的批次擾動和噪聲較大時,文獻[42]提出了基于觀測器的最優學習控制律

其中?uk=uk?uk?1,K是個濾波增益矩陣.

最近,文獻[92]提出一種離散時間迭代學習Kalman濾波方法,將Kalman濾波與迭代學習控制相結合,對系統狀態進行估計,為基于觀測器的最優迭代學習控制的設計提供了新的思路.

在很多工業過程控制應用中,為了保證安全性,平滑操作等,總需要對過程變量施加以限制.通常,對輸入和輸出的約束比較普遍,有如下幾種形式:

1)對輸入值的約束

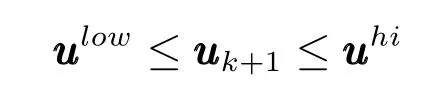
2)對輸入關于時間變化率的限制

3)對輸入關于批次變化率的限制

當用連續的線性近似來描述非線性間歇過程時,上述約束條件能夠有效地將輸入信號限制在線性范圍內.

4)對于系統輸出,通常增加如下軟約束:

文獻[42]將這些約束條件轉化成如下線性矩陣不等式:

從而,輸入輸出受限的線性系統的最優迭代學習控制律即為如下性能指標函數在上述約束不等式條件下的可行解

最近,很多學者提出了基于模型預測控制的迭代學習控制[52?57],在最優問題中充分考慮并結合了系統的輸入輸出約束.進一步,文獻[91]提出了多變量約束的間歇過程的迭代學習模型預測控制方法,綜合考慮了系統的約束問題、時變問題、外界擾動和隨機特征等因素.文獻[93]基于間歇過程的二維分段線性化描述,通過線性矩陣不等式求解,提出了一種受限迭代學習控制方法,提高了控制性能.

近年來,多中間關鍵點跟蹤控制和以間歇過程產品質量控制為主的終端跟蹤控制的研究成為迭代學習控制的另一個熱點問題.文獻[94]將基于范數優化的迭代學習控制策略引入到終端跟蹤控制任務,提出了最優終端迭代學習控制(Optimal terminal iterative learning control,OTILC)方法.文獻[95?97]提出了基于優化的點到點迭代學習控制(Point-to-point iterative learning control,PTPILC)方法,僅跟蹤指定的參考點而不是參考軌跡上的所有點.另外,文獻[90]討論了輸入輸出約束的問題.文獻[98]針對線性連續時間系統的多中間關鍵點的跟蹤問題,提出了范數最優迭代學習方法.

最優迭代學習控制的研究中,還有一類基于參數優化的迭代學習控制(Parameter optimal iterative learning control,POILC)方法,由Owens等[99]首先提出,主要目的是為了在保證算法具有單調收斂性的前提下,減少每次迭代時的計算量.文獻[100]研究了系統輸入輸出矩陣的正定性與跟蹤誤差單調收斂的關系.文獻[101]提出了基于逆模型的魯棒POILC算法.文獻[102]研究了梯度下降的魯棒POILC算法.Owens[103]以多輸入多輸出線性系統為研究對象,將范數最優和參數最優迭代學習控制算法進行了統一描述,提出了一種新的最優迭代學習控制方法.

近年來,高階迭代學習控制算法[104?106]也吸引了學者們的廣泛關注,可以利用更多以前操作的控制知識,提高系統的控制性能.文獻[106]是文獻[99]參數優化迭代學習控制的擴展.如果系統是非正定的,可通過在算法中增加合適的基函數,保證跟蹤誤差單調收斂為零.

由式(5)可以看出,基于超向量技術的范數最優迭代學習控制的輸入輸出矩陣G的維數不僅跟間歇過程的變量相關,還會隨著操作/批次長度而急劇增長,因此控制算法(5)在長時間區間內的執行和計算是非常耗時的,并且需要更多的存儲單元.因此,近年來一些學者[107?111]開始研究基于Lifted描述的最優迭代學習控制的高效計算問題.文獻[112]提出了一種基于非Lifted描述的最優迭代學習控制方法,在系統輸入輸出描述中不再使用超向量技術,很大程度上降低了算法的計算復雜度.

如前所述,非線性系統的最優迭代學習控制本質上依賴于對非線性系統的線性化估計的顯性表達.例如,賈立等[113]利用神經模糊模型提出了間歇過程無約束迭代學習控制方法.李恒杰等[114]提出基于克隆選擇算法的非線性優化迭代學習控制.逄勃等[115]將擬Broyden法和參數優化迭代學習控制方法結合,提出了單調收斂的迭代學習控制算法.

2 數據驅動的迭代動態線性化方法

在實際控制應用中,許多非線性系統模型,例如Hammerstein模型、雙線性模型等,都可以表示為如下輸入輸出的一般非線性遞歸形式:

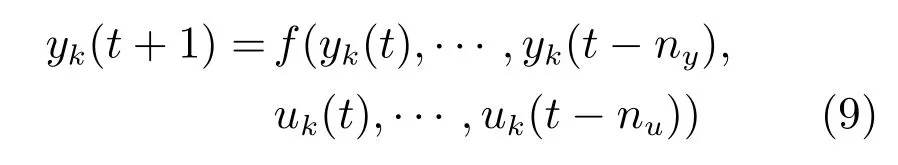
其中yk(t)和uk(t)是系統的輸出和輸入;f(·)是未知的非線性函數且連續可微;ny和nu是兩個正整數,分別表示系統輸出和輸入的階數,不失一般性,假設nu＜ny;t∈{0,···,N}表示離散時間,N是個正整數表示有限時間區間的終點;k∈{0,1,···,∞}表示迭代次數.

非線性系統的控制器設計和分析本質上都是顯式或隱式地利用各種數學技巧,將非線性問題轉化為線性或類似線性的問題來處理,數據驅動的最優ILC的研究也不例外.因此,本節主要回顧非線性系統的數據驅動的迭代動態線性化方法,以方便讀者閱讀,并為后續的數據驅動的最優ILC的分析奠定基礎.

在后面討論中,嚴格起見,設對所有t＜0,uk(t)=0且yk(t)=0.另外,系統(1)滿足如下兩個假設.

假設1.系統的初始狀態yk(0)在所有迭代中固定不變,即yk(0)=c,?k∈Z+,其中c是個常數.

假設 2.非線性函數f(·)滿足全局Lipschitz條件,即,

注1.假設1是迭代學習控制分析中常用的條件,意味著被控系統在每次運行時都必須從相同位置開始.

因為t∈{0,···,N}是有限的離散時間區間,根據式(9),可以將非線性系統的輸出序列重新用初始狀態和系統輸入逐點描述如下[70?72]:

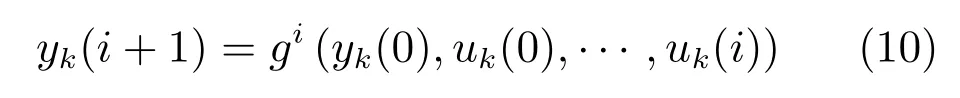
其中gi(·),i=0,···,N? 1是f(·)的復合函數.

注 2.這里僅需要已知gi(·),i=0,···,N?1的存在性而不需要知道其精確表達.只要f(·)存在,作為其對應的復合函數,gi(·)也一定存在.根據高等數學基礎知識,可以知道gi(·)具有和非線性函數f(·)相同的性質,例如連續性、可微性、有界性等.

為描述簡單,定義三個向量如下:

那么,考慮所有i=0,···,N?1的情況,由方程(10)可得如下輸入輸出的向量表達形式

根據注2,可將假設2稍微修改如下.

假設2′.非線性向量值函數g(·) 滿足全局 Lipschitz,即,

其中Lx＜∞和Lu＜∞是兩個正李普希茲常數.

定理1.對一般非線性離散時間系統(1),在滿足假設1和2的條件下,一定存在一個系統非線性關于控制輸入的偏導數矩陣Φk,使得非線性系統(1)可轉化為如下迭代動態線性形式,

定理1的證明參見文獻[76?78].

注3.迭代動態線性化數據模型(12)與原未知非線性系統(9)在輸入輸出數據行為上是等價的、精確的,沒有省略任何高階項.該迭代動態線性化數據模型是隨工作點批次變化而變化的動態模型而非靜態近似模型.該數據模型中不包含受控系統的數學模型、階數、時滯等先驗知識.由于系統的所有動力學行為信息都隱含在系統的輸入輸出數據中,因此該數據模型中沒有傳統意義下的未建模動態.

注4.迭代動態線性化模型(12)建立了重復動態系統沿迭代軸方向的系統輸出變化和輸入變化之間的關系,而不是沿時間軸方向的變化關系.形式上,被控系統的時間動態特性似乎是被忽略了,但其實質上是包含在未知梯度信息Φk中.系統本身仍舊是沿時間軸運行,時間動態特性可很容易地由系統的實時狀態而反應.未知梯度參數Φk具有迭代-時間二維動態特性,可利用測量的I/O數據進行估計.

注 5.迭代動態線性化方法是數據驅動的,不需要任何關于系統的模型信息,是直接面向控制系統設計的線性化方法.該動態線性化方法獲得的數據模型具有模型簡單、不丟失任何信息、包含參數少、具有增量形式等特點,是目的于控制系統設計的數據模型,或稱為控制器設計模型,而非機理模型.

注6.迭代動態線性化數據模型形式簡單,是一種梯度參數線性結構,因此很多基于模型的迭代學習控制的設計技術和分析工具都可以借鑒而提出各種新的數據驅動迭代學習控制方法,例如可以采用自適應技術或最優技術.

注7. 迭代動態線性化是研究數據驅動迭代學習控制理論的最重要工具之一.它提供了基于控制目的而研究系統閉環和開環數據的一種新方法,可認為是系統開環和閉環中數據關系的一種建模,這對未來信息豐富的復雜系統的控制理論是至關重要的.

3 數據驅動的最優迭代學習控制

在工業實際應用中,通常有三類不同的控制任務.第一類控制任務是最普遍的跟蹤完整的參考軌跡的任務,要求系統輸出必須跟蹤整個軌跡上的所有點.第二類任務是跟蹤多個中間參考點,僅對指定時刻參考點處的跟蹤誤差有精度要求,而不是構成完整參考軌跡的所有點.第三類任務的控制目標僅僅是系統運行終端的狀態或輸出,使其調節以達到期望值.在第二類和第三類控制任務中,有些控制背景中,非指定點處的系統狀態和輸出可能是不可測的.

對于第二類控制任務,有些學者專門提出了點到點迭代學習控制(PTPILC)方法[94?98],僅利用指定點處的輸出誤差信息對控制行為進行迭代修正.文獻[16?18,94]則針對第三類控制任務提出了終端迭代學習控制(TILC)策略,僅利用了系統運行終點的終端輸出誤差.

需要注意的是,如果系統狀態和輸出在所有時刻點均可測,則可以通過設計一條通過指定期望參考點的最優軌跡,以此可將標準的迭代學習控制用于第二和第三類控制任務中,使系統輸出跟蹤所設計的最優參考軌跡.然而,問題在于通過指定參考點的參考軌跡的設計非常困難,并且當被控系統本身有所變化時,很難保障所設計的參考軌跡仍舊是最優的.

另外,PTPILC和TILC去除了不必要的參考點上的跟蹤性能約束限制,可獲得額外自由度提高控制性能,例如降低控制能量、加快收斂速度和減少存儲單元等.因此,PTPILC和TILC方法是面向實際應用問題提出的,具有重要的意義而不是傳統ILC方法的簡單推廣.

文獻[77]針對一類未知的非線性離散時間系統,提出了數據驅動的最優迭代學習控制(DDOILC)以及相應的數據驅動最優點對點迭代學習控制(DDOPTPILC)和數據驅動的最優終端迭代學習控制(DDOTILC)方法,具有完整的設計框架和分析方法,包括迭代動態線性化、壓縮映射分析方法、梯度參數估計方法等.

本節主要以數據驅動的迭代動態線性化方法為基礎,回顧了數據驅動的廣義最優迭代學習控制方法,包括軌跡跟蹤任務、多中間點跟蹤任務、單終端點跟蹤任務,以方便讀者較為全面地理解這類具有較完整理論基礎的學習控制系統的設計和分析過程.

3.1 完整軌跡跟蹤的DDOILC

針對完整軌跡跟蹤的控制任務,文獻[77]利用最優控制原理提出了一種數據驅動的最優迭代學習控制(DDOILC)方法,由式(13)～(15)構成,

其中λ＞0,μ＞0表示權重因子;ρ ＞0,η∈(0,2)表示步長因子,其加入是為了使算法(13)和(15)更具有一般性且方便收斂性分析;0(t)表示(t)的初值;k(i)表示向量k(t)的第i個元素,i=0,1,···,t;ε是個非常小的正數.

DDOILC方法的收斂性和穩定性定理及證明參見文獻[77],并且該方法可很容易地推廣到多輸入多輸出系統.

注8.重置算法(14)是用來增強參數估計算法(16)跟蹤迭代變化參數的能力.在選擇初值時,要使與?k(t)所有元素的符號保持相同.

注9.學習控制律(15)的學習增益是迭代-時間變化的,只需要量測的I/O數據利用估計算法(13)和重置算法(14)獲得.

注10.與傳統的最優ILC方法相比,DDOILC(13)～(15)稱作是數據驅動或基于數據的控制策略.控制器的設計和分析僅依賴于系統的I/O數據,不需要已知任何被控對象的模型信息.但是,數據驅動控制并不意味著要排斥基于模型的控制方法,二者應該是相互補充和輔助的關系.如果已知被控系統的精確線性模型,基于模型的控制方法應該是首選,可充分利用已知的模型信息而實現更好的控制效果.相反,數據驅動的方法則不能利用已知的系統模型信息.文獻[77]用精確已知的線性模型作為仿真實例,證明了基于模型的NOILC控制性能要優于DDOILC.

注11.盡管DDOILC方法不論是在學習控制器的形式上還是在基于壓縮映射方法的收斂性分析上,都與傳統的PID-型迭代學習控制極為相似,但是DDOILC的學習增益是迭代變化的且能利用所測量的實時I/O數據進行迭代整定.因此,DDOILC在處理不確定性方面要優于傳統的PID型ILC.

注12.DDOILC與傳統的最優ILC也非常相似.二者都是基于最優二次性能指標而設計的,都可實現沿迭代方向的單調收斂性.然而,DDOILC是針對未知非線性系統提出的,而不是精確已知的線性系統.因此,DDOILC是數據驅動的方法,傳統的最優ILC是基于模型的方法.

注13.由注11和注12中的分析可知,基于壓縮映射的PID型ILC和基于目標函數的最優ILC都可以被看作是DDOILC的特例,并且DDOILC在處理強非線性、高不確定性、迭代變化擾動等問題時,可實現更好的控制性能.文獻[116]已通過仿真結果證實,當系統的模型擾動較大時,應用基于模型的OILC方法,跟蹤誤差的收斂性將不再保證,甚至發散.而DDOILC方法在系統模型出現大的變化時,仍能保障跟蹤誤差的收斂性.

3.2 多中間點跟蹤的DDOPTPILC

對點到點跟蹤任務,假設在系統運行的有限時間區間{1,2,···,N}上,僅在指定點{t1,t2,···,tM}處,要求系統輸出跟蹤期望值yd(t1),yd(t2),···,yd(tM).

在指定點{t1,t2,···,tM}處,系統的輸出可重新表述為[77]:

其中m=1,···,M.

其中λ＞0,μ＞0表示權重因子;ρ＞0,η∈(0,2)表示步長因子;m=1,···,M;ε是個很小的正數;的估計;的初值;表示的第i個元素.

注 14.與 DDOILC(13)～(15)相比,DDOPTPILC(18)～(20)僅利用在指定時刻點的誤差信息,從而可用于系統輸出僅在指定時刻點可測的控制背景,并且由于去除了不必要點上的跟蹤性能約束,可一定程度上加快收斂速度、降低控制能量、減少存儲單元.這在文獻[77]仿真中已經得到驗證.

3.3 終端點跟蹤的DDOTILC

終端迭代學習控制的目標是系統運行終端的狀態或終端輸出,而不是跟蹤整個軌跡.換句話說,尋找合適的控制輸入序列使得系統的終端輸出yk(N)在系統運行終點跟蹤期望值yd,當迭代次數k趨于無窮時,終端跟蹤誤差ek(N)=yd?yk(N)收斂于0.

系統運行終點的終端輸出可重新表示為[76?77],

其中yk(N)表示系統在迭代運行終點的輸出.

類似地,終端迭代動態線性化形式為[76?77]對于單個點的終端跟蹤任務,文獻[77]給出了一種數據驅動的最優終端迭代學習控制(DDOTILC)方法:

其中λ＞0,μ＞0表示權重因子;ρ＞0,η∈(0,2)表示步長因子;ε是個很小的正常數;0(N?1)表示k(N?1)的初始估計值.

注15.DDOTILC(23)～(25)算法中僅利用了系統運行終點的終端輸出跟蹤誤差,去掉了在其他點上不必要的限制,從而可提高控制性能.如文獻[77]所示,不論在收斂速度、控制能量和收斂精度上都優于DDOILC方法.

3.4 DDOILC的關鍵問題和應用研究

DDOILC方法應用中遇到的一些重要問題,如隨機初始條件、高階控制律、控制性能的增強、迭代變化參考軌跡等,也在最近的一些文獻中進行了充分研究.

在實際間歇過程的應用中,產品的質量要求會根據市場、用戶等需求而作調整,因此期望軌跡并不是在所有操作中都保持相同.文獻[117]首先考慮了隨迭代變化的期望參考點,提出了數據驅動的自適應最優終端ILC方法,但跟蹤誤差的收斂性分析仍舊依賴于相同初始條件的假設.由于定位精度、量測精度以及狀態擾動等原因,相同初始條件在實際中很難滿足,很大程度上阻礙了DDOILC的應用.因此,文獻[118?119]和文獻[120]分別用神經網絡和高階內模來近似逼近隨機迭代變化的初始條件對系統運行終端輸出的影響,并用于控制器設計作為補償,其中期望軌跡和初始狀態都是隨迭代次數變化的.文獻[121]則直接將隨機初始狀態作為未知參數進行迭代估計,得到了跟蹤誤差的有界收斂性.

文獻[78]針對終端迭代學習控制任務,研究了當系統狀態額輸出在終端點以外的時刻點均不可測時,如何利用更多的控制信息來提高控制性能,提出了增強的數據驅動終端迭代學習控制方法.高階迭代學習控制律因為能夠利用更多以前操作中獲得的控制信息實現更好的控制性能也受到了重視.文獻[122?123]通過改進控制性能指標函數,提出了高階的數據驅動最優迭代學習控制方法.

關于實際工程應用中經常遇到的輸入輸出受限問題以及計算復雜度問題,也已在最近的工作中進行了研究,提出了相應的解決方案[116].

DDOILC方法已進行了廣泛的實驗驗證和仿真分析,說明了這些方法的有效性,例如化學間歇過程[76?78,121?123]、快速路交通系統[124?126]、自動列車停車控制[127]等.數據驅動的迭代學習控制將成為以間歇過程為主的、越來越復雜、規模越來越大的執行重復生產的工業控制的主要方法,有著廣泛的理論研究前景和潛在的應用價值.

3.5 其他數據驅動的學習控制方法

目前,數據驅動的學習控制策略的設計和分析引起了國內外學者的關注.文獻[128?129]針對線性時不變系統,借助于有限脈沖響應濾波技術,提出了一種數據驅動的迭代學習控制方法,系統的脈沖響應模型可由以前迭代運行獲得的輸入輸出數據進行估計.系統的控制性能主要依賴于脈沖響應模型的估計精度.如果要嚴格地保證脈沖響應模型的估計值等于系統輸出的真實值,要求被控系統是線性時不變的,且沒有量測噪聲和其他干擾存在.

文獻[130?131]利用迭代學習控制的優點,提出了基于實驗隨機搜索算法的無模型數據驅動迭代參考輸入整定方法,并且考慮了系統的輸入輸出受限情況,但是控制器的設計和分析也是基于線性時不變系統而提出的,所采用的也是迭代反饋整定的策略.

文獻[64]提出了受限非線性系統的模最優ILC的一般形式,模型校正可顯性地估計,性能指標函數采用直接最優控制方法進行最小化,由此得到非線性規劃問題并給出了該問題的有效求解策略.需要說明的是,控制器的設計和分析是基于非線性系統的線性估計模型進行的.

文獻[132]研究了重復脈沖噪聲的主動控制方法,基于快速傅里葉變換,提出了未知或時變次級路徑信號噪聲主動抑制系統的無模型迭代學習控制算法.與基于模型的方法不同,控制器的設計僅依賴于輸入輸出數據而不需要系統模型的知識.

文獻[133]提出了雙迭代Q-學習算法,其中內部迭代可以最小化每個周期的總的功率負載指標;外部迭代可以使Q函數迭代地收斂到最優值.

文獻[134]在研究混雜控制系統結構時,提出了多輸入多輸出系統的最優行為預測機制,給出了一種數據驅動無模型迭代學習控制方法,其中閉環反饋控制器采用虛擬參考整定(Virtual reference feedback tuning,VRFT)方法設計,期望的新軌跡可被逼近且最優參考輸入可被重置.

4 結論與展望

本文簡要回顧了間歇過程的最優迭代學習控制方法,包括基于模型的最優迭代學習控制和數據驅動的最優迭代學習控制,目的在于借鑒前者研究和分析中常用的方法,找到后者研究中可突破的途徑.數據驅動的最優迭代學習控制的關鍵是迭代動態線性化,因此詳細討論了迭代動態線性化的特征和對應控制器的設計.

迭代動態線性化方法僅依賴于被控系統的I/O數據,因此,在迭代動態線性化過程中,沒有建模誤差,也沒有未建模動態,所產生的迭代動態線性化數據模型是完全等價于原非線性系統的,使得在基于模型的控制方法中廣泛存在的未建模動態和系統魯棒性這一矛盾體不再存在.

傳統的近似線性化方法或精確線性化在實際中很難實現.相反,迭代動態線性化僅依賴系統的I/O數據即可得到,且數據模型本身是可根據實時I/O數據進行估計和更新的.因此,等價的迭代動態線性化是DDOILC方法的基礎,將成為新的分析非線性重復系統的重要工具.

數據驅動最優迭代學習控制或者數據驅動控制[135]方法的目標是直接利用過程數據或由數據中獲取的知識來設計控制器,去除基于模型的最優迭代學習控制或基于模型的控制方法中極具挑戰性的問題,例如,建模困難性、未建模動態和魯棒性,最終減小或消除基于模型的控制方法與實際應用之間存在的鴻溝.需要強調的是,數據驅動控制方法并不意味著要排除基于模型的控制方法.相反,如果存在被控對象的可靠的精確線性模型,基于模型的方法則是首選.

基于模型的最優迭代學習控制的研究已經非常成熟,具有系統的理論分析方法.相反,數據驅動的最優迭代學習控制主要是針對不能或難以獲得被控系統模型的控制系統的設計方法,其研究還處于起始階段.為了數據驅動最優迭代學習控制的健康發展,還需要大量的研究工作和努力,并且這些工作也將是極具挑戰性的.

4.1 線性系統設計方法和分析工具的引入

從典型控制系統設計方法的本質上講,非線性系統的最優迭代學習控制設計也是利用某些數學分析的技巧千方百計地利用系統數學模型結構和形式將其受控系統的控制輸入變量顯式地表述出來,這個過程本質上就是對控制輸入的線性化,即,基于模型的最優迭代學習控制方法本質上也是某種線性化的方法.從這個觀點上看,數據驅動的與基于模型的最優迭代學習控制的研究和設計思路在本質上是一樣的,只是數據驅動的最優迭代學習控制的研究起始于未知非線性重復系統的迭代動態線性化方法.因此,在今后工作中可借鑒更多基于模型的最優迭代學習控制的設計方法和分析工具,以處理工業應用中遇到的更多實際問題,如隨機不確定性、分布式系統、協同問題等.

4.2 系統穩定性、收斂性、魯棒性的分析

因為數據驅動的最優迭代學習控制理論是直接從I/O數據到控制器的,沒有基于機理或系統辨識的建模過程,因此,與基于模型的方法不同,其穩定性、收斂性和魯棒性分析應該也是直接基于I/O數據的.實質上,數據驅動框架下的魯棒性就是研究系統采樣、系統數據測量噪聲、數據處理以及數據在傳輸過程中的丟包、亂碼、延時等對已設計的數據驅動控制系統所具有性質的保持程度和影響.大數據環境下,比較有前景的系統穩定性、收斂性、魯棒性的分析方法可能是基于數據能量有界及壓縮映射的方法.

4.3 面向控制的數據處理技術

在線和離線數據都包含了大量有價值的系統動力學知識以及系統運行規律和模式.因此,探討如何利用系統的I/O數據和系統規律進行數據驅動最優迭代學習控制的設計具有重要意義.所以,面向控制的有效數據處理方法將是非常有前景和重要的研究方向之一.

4.4 基于模型的與數據驅動的最優ILC的綜合設計

每個控制方法,不管是基于模型的還是數據驅動的,都具有他們各自的優勢和劣勢,不能被其他方法完全取代.最直接有效的方法就是讓不同的控制方法按照互補的方式一起工作,取長補短.當被控對象機理模型模型較為清楚,且適合于設計控制器時,顯然基于模型的最優ILC方法的控制性能、可靠性等性質都是占優的.相反,如果被控對象的機理模型存在很大不確定性,且對外界的擾動等因素變化較為敏感,那么基于數據驅動的最優ILC方法則更為適合.因此,如何定量地描述基于模型的控制策略對系統外界不確定性的抑制程度,如何確定基于模型的控制策略和數據驅動的控制策略之間相互切換的有效機制,實現控制系統的可靠性和控制精度等全方面的改進,也將是今后研究的熱點方向和挑戰性問題.

1 Bonvin D.Control and optimization of batch processes.IEEE Control Systems,2006,26(6):34?45

2 Tomazi K,Linninger A A,Daniel J R.Batch processing industries.Batch Processes.Boca Raton,FL:CRC Press,2006.7?39

3 Tchobanoglous G,Burton F G,Stensel H D.Wastewater Engineering:Treatment and Reuse.New York:McGraw-Hill,2003.

4 Young R A,Akhtar M.Environmentally Friendly Technologies for the Pulp and Paper Industry.New York:Wiley,1998.

5 Mazurek J,Ashford N A.Making Microchips:Policy,Globalization,and Economic Restructuring in the Semiconductor Industry.Cambridge,MA:MIT Press,1998.

6 McCormick K.Manufacturing in Global Pharmaceutical Industry.London:Urch,2003.

7 Myerson A S.Handbook of Industrial Crystallization.London,UK:Butterworths-Heinemann,2001.

8 Seborg D E,Edgar T F,Mellichamp D A.Process Dynamics and Control.New York:Wiley,2004.

9 Nagy Z K,Braatz R D.Robust nonlinear model predictive control of batch processes.AIChE Journal,2003,49(7):1776?1786

10 Moore K L.Iterative Learning Control for Deterministic Systems.London,UK:Springer-Verlag,1993.

11 Sun Hai-Qiao.Research on robust iterative learning control applied to batch process[Master dissertation],Jiangnan University,China,2014.(孫海喬.間歇過程的魯棒迭代學習控制研究[碩士學位論文],江南大學,中國,2014.)

12 Wang Jing,Wang Yue,Wang Wei,Cao Liu-Lin,Jin Qi-Bing.Adaptive iterative learning control based on unfalsified strategy applied in batch process.Journal of Central South University(Science and Technology),2015,46(4):1318?1325(王晶,王玥,王偉,曹柳林,靳其兵.基于去偽策略的間歇過程自適應迭代學習.中南大學學報 (自然科學版),2015,46(4):1318?1325)

13 Fran?cois G,Srinivasan B,Bonvin D.Use of measurements for enforcing the necessary conditions of optimality in the presence of constraints and uncertainty.Journal of Process Control,2005,15(6):701?712

14 Del Castillo E,Hurwitz A M.Run-to-run process control:literature review and extensions.Journal of Quality Technology,1997,29(2):184?196

15 Sachs E,Guo R S,Ha S,Hu A.Process control system for VLSI fabrication.IEEE Transactions on Semiconductor Manufacturing,1991,4(2):134?144

16 Xu J X,Chen Y Q,Lee T H,Yamamoto S.Terminal iterative learning control with an application to RTPCVD thickness control.Automatica,1999,35(9):1535?1542

17 Flores-Cerrillo J,MacGregor J F.Iterative learning control for final batch product quality using partial least squares models.Industrial&Engineering Chemistry Research,2005,44(24):9146?9155

18 Gauthier G,Boulet B.Terminal iterative learning control design with singular value decomposition decoupling for thermoforming ovens.In:Proceedings of the 2009 American Control Conference.St.Louis,MO,USA:IEEE,2009.1640?1645

19 Arimoto S,Kawamura S,Miyazaki F.Bettering operation of robots by learning.Journal of Robotic Systems,1984,1(2):123?140

20 Lee K S,Bang S H,Chang K S.Feedback-assisted iterative learning control based on an inverse process model.Journal of Process Control,1994,4(2):77?89

21 Lee K S,Bang S H,Yi S,Son J S,Yoon S C.Iterative learning control of heat-up phase for a batch polymerization reactor.Journal of Process Control,1996,6(4):255?262

22 Liu T,Gao F R.Robust two-dimensional iterative learning control for batch processes with state delay and time-varying uncertainties.Chemical Engineering Science,2010,65(23):6134?6144

23 Wang Y Q,Liu T,Zhao Z.Advanced PI control with simple learning set-point design:application on batch processes and robust stability analysis.Chemical Engineering Science,2012,71:153?165

24 Wang Y Q,Zisser H,Dassau E,Jovanovic L,Doyle III F J.Model predictive control with learning-type set-point:application to arti ficial pancreaticβ-cell.AIChE Journal,2010,56(6):1510?1518

25 Liu T,Wang X Z,Chen J H.Robust PID based indirecttype iterative learning control for batch processes with timevarying uncertainties.Journal of Process Control,2014,24(12):95?106

26 Márquez-Vera M A,Ramos-Velasco L E,Suárez-Cansino,Márquez-Vera C A.Fuzzy iterative learning control applied in a biological reactor using a reduced number of measures.Applied Mathematics and Computation,2014,246:608?618

27 Gao F R,Yang Y,Shao C.Robust iterative learning control with applications to injection molding process.Chemical Engineering Science,2001,56(24):7025?7034

28 Shi J,Gao F R,Wu T J.Robust design of integrated feedback and iterative learning control of a batch process based on a 2D Roesser system.Journal of Process Control,2005,15(8):907?924

29 Shi J,Gao F R,Wu T J.Integrated design and structure analysis of robust iterative learning control system based on a two-dimensional model.Industrial&Engineering Chemistry Research,2005,44(21):8095?8105

30 Shi J,Gao F R,Wu T J.A robust iterative learning control design for batch processes with uncertain perturbation and initialization.AIChE Journal,2006,52(6):2171?2187

31 Hao S L,Liu T,Paszke W,Galkowski K.Robust iterative learning control for batch processes with input delay subject to time-varying uncertainties.IET Control Theory&Applications,2016,10(15):1904?1915

32 Tan K K,Zhao S,Huang S N,Lee T H,Tay A.A new repetitive control for LTI systems with input delay.Journal of Process Control,2009,19(4):711?716

33 Xu J X,Xu J.On iterative learning from different tracking tasks in the presence of time-varying uncertainties.IEEE Transactions on Systems,Man,and Cybernetics,Part B,Cybernetics,2004,34(1):589?597

34 Sun M X,He X X.Iterative learning identi fication and control of discrete time-varying systems.In:Proceedings of the 2017 Chinese Control Conference.Zhangjiajie,Hunan,China:IEEE,2017.520?524

35 Chi R H,Hou Z S,Xu J X.Adaptive ILC for a class of discrete-time systems with iteration-varying trajectory and random initial condition.Automatica,2008,44(8):2207?2213

36 Tayebi A.Adaptive iterative learning control for robot manipulators.Automatica,2004,40(7):1195?1203

37 Sun M X,Ge S S.Adaptive repetitive control for a class of nonlinearly parametrized systems.IEEE Transactions on Automatic Control,2006,51(10):1684?1688

38 Li X D,Xiao T F,Zheng H X.Adaptive discrete-time iterative learning control for non-linear multiple input multiple output systems with iteration-varying initial error and reference trajectory.IET Control Theory&Applications,2011,5(9):1131?1139

39 Yan W L,Sun M X.adaptive iterative learning control of discrete-time varying systems with unknown control directions.International Journal of Adaptive Control and Signal Processing,2013,27(4):340?348

40 Chi R H,Hou Z S,Jin S T.A data-driven adaptive ILC for a class of nonlinear discrete-time systems with random initial states and iteration-varying target trajectory.Journal of the Franklin Institute,2015,352(6):2407?2424

41 Amann N,Owens D H,Rogers E.Iterative learning control for discrete-time systems with exponential rate of convergence.IEE Proceedings-Control Theory and Applications,1996,143(2):217?224

42 Lee J H,Lee K S,Kim W C.Model-based iterative learning control with a quadratic criterion for time-varying linear systems.Automatica,2000,36(5):641?657

43 Moore K L,Verwoerd M H A.l1-optimal robust iterative learning controller design.In:Proceedings of the 2008 American Control Conference.Seattle,WA,USA:IEEE,2008.3881?3886

44 Xu J X,Tan Y.Robust optimal design and convergence properties analysis of iterative learning control approaches.Automatica,2002,38(11):1867?1880

45 Sanzida N,Nagy Z K.Iterative learning control for the systematic design of supersaturation controlled batch cooling crystallisation processes.Computers&Chemical Engineering,2013,59:111?121

46 Axelsson P,Karlsson R,Norrlf M.Estimation-based normoptimal iterative learning control.Systems&Control Letters,2014,73:76?80

47 Nguyen D H,Banjerdpongchai D.An LMI approach for robust iterative learning control with quadratic performance criterion.Journal of Process Control,2009,19(6):1054?1060

48 Lim I,Barton K L.Pareto iterative learning control:optimized control for multiple performance objectives.Control Engineering Practice,2014,26(1):125?135

49 Chu B,Owens D H.Accelerated norm-optimal iterative learning control algorithms using successive projection.International Journal of Control,2009,82(8):1469?1484

50 Tousain R,van der Meche E,Bosgra O.Design strategy for iterative learning control based on optimal control.In:Proceedings of the 40th IEEE Conference on Decision and Control.Orlando,FL,USA:IEEE,2001,5:4463?4468

51 Liu Shan,Wu Tie-Jun.Iterative learning control based on optimization criterion.In:Proceedings of the 4th World Congress on Intelligent Control and Automation.Shanghai,China,2002.621?625(劉山,吳鐵軍.基于最優化指標的迭代學習控制.第四屆全球智能控制與自動化大會(WCICA002).上海,2002.621?625)

52 Chen C,Xiong Z H,Zhong Y S.Design and analysis of integrated predictive iterative learning control for batch process based on two-dimensional system theory.Chinese Journal of Chemical Engineering,2014,22(7):762?768

53 Mishra S,Topcu U,Tomizuka M.Optimization-based constrained iterative learning control.IEEE Transactions on Control Systems Technology,2011,19(6):1613?1621

54 Amann N,Owens D H,Rogers E.Predictive optimal iterative learning control.International Journal of Control,1998,69(2):203?226

55 Lee K S,Chin I S,Lee H J,Lee J H.Model predictive control technique combined with iterative learning for batch processes.AIChE Journal,1999,45(10):2175?2187

56 Wang L P,Freeman C T,Chai S,Rogers E.Predictiverepetitive control with constraints: from design to implementation.Journal of Process Control,2013,23(7):956?967

57 Jin S T,Hou Z S,Chi R H.A novel data-driven terminal iterative learning control with iteration prediction algorithm for a class of discrete-time nonlinear systems.Journal of Applied Mathematics,2014,2014:Article No.307809

58 Chin I,Qin S J,Lee K S,Cho M.A two-stage iterative learning control technique combined with real-time feedback for independent disturbance rejection.Automatica,2004,40(11):1913?1922

59 Slotine J J E,Li W P.Applied Nonlinear Control.Englewood Cliffs,NJ,USA:Prentice Hall,1991.

60 Chen L J,Narendra K S.Identi fication and control of a nonlinear discrete-time system based on its linearization:a uni fied framework.IEEE Transactions on Neural Networks,2004,15(3):663?673

61 Xi Yu-Geng,Wang Fan.Nonlinear multi-model predictive control.Acta Automatica Sinica,1996,22(4):456?461(席裕庚,王凡,非線性系統預測控制的多模型方法,自動化學報,1996,22(4):456?461)

62 Deng H,Li H X,Wu Y H.Feedback-linearization-based neural adaptive control for unknown nonaffine nonlinear discrete-time systems.IEEE Transactions on Neural Networks,2008,19(9):1615?1625

63 Dumont G A,Fu Y.Non-linear adaptive control via laguerre expansion of volterra kernels.International Journal of Adaptive Control and Signal Processing,1993,7(5):367?382

64 Volckaert M,Diehl M,Swevers J.Generalization of norm optimal ILC for nonlinear systems with constraints.Mechanical Systems and Signal Processing,2013,39(1?2):280?296

65 Yan Qiu-Zhen,Sun Ming-Xuan.Suboptimal learning control for nonlinear systems with both parametric and nonparametric uncertainties.Acta Automatica Sinica,2015,41(9):1659?1668(嚴求真,孫明軒.非線性不確定系統準最優學習控制.自動化學報,2015,41(9):1659?1668)

66 Endelt B.Design strategy for optimal iterative learning control applied on a deep drawing process.The International Journal of Advanced Manufacturing Technology,2017,88(1):3?18

67 Wang D G,Song W Y,Shi P,Li H X.Approximation to a class of non-autonomous systems by dynamic fuzzy inference marginal linearization method.Information Sciences,2013,245:197?217

68 Xiong Z H,Zhang J.A batch-to-batch iterative optimal control strategy based on recurrent neural network models.Journal of Process Control,2005,15(1):11?21

69 Liu X J,Kong X B.Nonlinear fuzzy model predictive iterative learning control for drum-type boiler-turbine system.Journal of Process Control,2013,23(8):1023?1040

70 Hou Zhong-Sheng,Xu Jian-Xin.On data-driven control theory:the state of the art and perspective.Acta Automatica Sinica,2009,35(6):650?667(侯忠生,許建新.數據驅動控制理論及方法的回顧和展望.自動化學報,2009,35(6):650?667)

71 Hou Z S,Jin S T.Model Free Adaptive Control:Theory and Applications.New York:CRC Press,2013.

72 Hou Zhong-Sheng.Highlight and perspective on model free adaptive control.Journal of Systems Science and Mathematical Sciences,2014,34(10):1182?1191(侯忠生.再論無模型自適應控制.系統科學與數學,2014,34(10):1182?1191)

73 Hou Z S,Wang Z.From model-based control to data-driven control:survey,classi fication and perspective.Information Sciences,2013,235:3?35

74 Yin S,Li X W,Gao H J,Kaynak O.Data-based techniques focused on modern industry:an overview.IEEE Transactions on Industrial Electronics,2015,62(1):657?667

75 Xu J X,Hou Z S.Notes on data-driven system approaches.Acta Automatica Sinica,2009,35(6):668?675

76 Chi R H,Wang D W,Hou Z S,Jin S T.Data-driven optimal terminal iterative learning control.Journal of Process Control,2012,22(10):2026?2037

77 Chi R H,Hou Z S,Huang B,Jin S T.A uni fied data-driven design framework of optimality-based generalized iterative learning control.Computers&Chemical Engineering,2015,77:10?23

78 Chi R H,Hou Z S,Jin S T,Wang D W,Chien C J.Enhanced data-driven optimal terminal ILC using current iteration control knowledge.IEEE Transactions on Neural Networks and Learning Systems,2015,26(11):2939?2948

79 Roman R C,Radac M B,Precup R E,Petriu E M.Datadriven model-free adaptive control tuned by virtual reference feedback tuning.Acta Polytechnica Hungarica,2016,13(1):83?96

80 Hou Z S,Liu S D,Tian T T.Lazy-learning-based datadriven model-free adaptive predictive control for a class ofdiscrete-timenonlinearsystems.IEEETransactions on Neural Networks and Learning Systems,2016,doi:10.1109/TNNLS.2016.2561702,to be published.

81 Hou Z S,Xu J X,Yan J W.An iterative learning approach for density control of freeway traffic flow via ramp metering.Transportation Research,Part C:Emerging Technologies,2008,16(1):71?97

82 Hou Z S,Xu J X,Zhong H W.Freeway traffic control using iterative learning control-based ramp metering and speed signaling.IEEE Transactions on Vehicular Technology,2007,56(2):466?477

83 Togai M,Yamano O.Analysis and design of an optimal learning control scheme for industrial robots:a discrete system approach.In:Proceedings of the 24th IEEE Conference on Decision and Control.Fort Lauderdale,FL,USA:IEEE,1985.1399?1404

84 Tao K M,Kosut R L,Aral G.Learning feedforward control.In:Proceedings of the 1994 American Control Conference.Baltimore,MD,USA:IEEE,1994,3:2575?2579

85 Gorinevsky D M.Direct learning of feedforward control for manipulator path tracking.In:Proceedings of the 1992 IEEE International Symposium on Intelligent Control.Glasgow,UK:IEEE,1992.42?47

86 Lee K S,Kim W C,Lee J H.Model-based iterative learning control with quadratic criterion for linear batch processes.Journal of Control Automation Systems Engineering,1996,2(3):148?157

87 Barton K L,Alleyne A G.A norm optimal approach to time-varying ILC with application to a multi-axis robotic testbed.IEEE Transactions on Control Systems Technology,2011,19(1):166?180

88 van de Wijdeven J,Donkers T,Bosgra O.Iterative learning control for uncertain systems:robust monotonic convergence analysis.Automatica,2009,45(10):2383?2391

89 Lee K S,Lee J H.Constrained model-based predictive control combined with iterative learning for batch or repetitive processes.In:Proceedings of the 2nd Asian Control Conference.Seoul,Korea:1997.33?36

90 Lee J H,Morari M,Garcia C E.State space interpretation of model predictive control.Automatica,1994,30(4):707?717

91 Oh S K,Lee J M.Iterative learning model predictive control for constrained multivariable control of batch processes.Computers&Chemical Engineering,2016,93:284?292

92 Cao Z X,Lu J Y,Zhang R D,Gao F R.Iterative learning Kalman filter for repetitive processes.Journal of Process Control,2016,46:92?104

93 Liu T,Wang Y Q.A synthetic approach for robust constrained iterative learning control of piecewise affine batch processes.Automatica,2012,48(11):2762?2775

94 Son T D,Ahn H S.Terminal iterative learning control with multiple intermediate pass points.In:Proceedings of the 2011 American Control Conference.San Francisco,CA,USA:IEEE,2011.3651?3656

95 Freeman C T,Cai Z L,Rogers E,Lewin P L.Iterative learning control for multiple point-to-point tracking application.IEEE Transactions on Control Systems Technology,2011,19(3):590?600

96 Freeman C T.Constrained point-to-point iterative learning control with experimental veri fication.Control Engineering Practice,2012,20(5):489?498

97 Son T D,Ahn H S,Moore K L.Iterative learning control in optimal tracking problems with speci fied data points.Automatica,2013,49(5):1465?1472

98 Owens D H,Freeman C T,Van Dinh T.Norm-optimal iterative learning control with intermediate point weighting:theory,algorithms,and experimental evaluation.IEEE Transactions on Control Systems Technology,2013,21(3):999?1007

99 Owens D H,Feng K.Parameter optimization in iterative learning control.International Journal of Control,2003,76(11):1059?1069

101 Harte T J,Htnen J,Owens D H.Discrete-time inverse model-based iterative learning control:stability,monotonicity and robustness.International Journal of Control,2005,78(8):577?586

102 Owens D H,Htnen J J,Daley S.Robust monotone gradient-based discrete-time iterative learning control.International Journal of Robust and Nonlinear Control,2009,19(6):634?661

103 Owens D H.Multivariable norm optimal and parameter optimal iterative learning control:a uni fied formulation.International Journal of Control,2012,85(8):1010?1025

104 Chen Y Q,Gong Z M,Wen C Y.Analysis of a high-order iterative learning control algorithm for uncertain nonlinear systems with state delays.Automatica,1998,34(3):345?353

105 Gunnarsson S,Norrlf M.On the disturbance properties of high order iterative learning control algorithms.Automatica,2006,42(11):2031?2034

107 Hakvoort W B J,Aarts R G K M,van Dijk J,Jonker J B.Lifted system iterative learning control applied to an industrial robot.Control Engineering Practice,2008,16(4):377?391

108 Rice J K,Verhaegen M.A structured matrix approach to efficient calculation of LQG repetitive learning controllers in the lifted setting.International Journal of Control,2010,83(6):1265?1276

109 Hakvoort W B J,Aarts R G K M,van Dijk J,Jonker J B.A computationally efficient algorithm of iterative learning control for discrete-time linear time-varying systems.Automatica,2009,45(12):2925?2929

110 Barton K L,Bristow D A,Alleyne A G.A numerical method for determining monotonicity and convergence rate in iterative learning control.International Journal of Control,2010,83(2):219?226

111 Haber A,Fraanje R,Verhaegen M.Linear computational complexity robust ILC for lifted systems.Automatica,2012,48(6):1102?1110

112 Sun H Q,Alleyne A G.A computationally efficient norm optimal iterative learning control approach for LTV systems.Automatica,2014,50(1):141?148

113 Jia Li, ShiJi-Ping, Qiu Ming-Sen, Yu Jin-Shou.Nonrestraint-iterative learning-based optimal control for batch processes.CIESR Journal,2010,61(8):1889?1894(賈立,施繼平,邱銘森,俞金壽.基于無約束迭代學習的間歇生產過程優化控制.化工學報,2010,61(8):1889?1894)

114 Li Heng-Jie,Hao Xiao-Hong,Zeng Xian-Qiang.Clonal selection algorithm based nonlinear optimal iterative learning control.Journal of Jilin University(Engineering and Technology Edition),2010,40(4):1054?1058(李恒杰,郝曉弘,曾賢強.基于克隆選擇算法的非線性優化迭代學習控制.吉林大學學報(工學版),2010,40(4):1054?1058)

115 Peng Bo,Shao Cheng.A robust iterative learning control with parameter-optimization for discrete nonlinear systems.Control and Decision,2014,29(3):449?454(逄勃,邵誠.一種參數優化的非線性離散系統魯棒迭代學習控制方法.控制與決策,2014,29(3):449?454)

116 Chi R H,Liu X H,Zhang R K,Hou Z S,Huang B.Constrained data-driven optimal iterative learning control.Journal of Process Control,2017,55:10?29

117 Chi R H,Wang D W,Lewis F L,Hou Z S,Jin S T.Adaptive terminal ILC for iteration-varying target points.Asian Journal of Control,2015,17(3):952?962

118 Liu T Q,Wang D W,Chi R H.Neural network based terminal iterative learning control for uncertain nonlinear nonaffine systems.International Journal of Adaptive Control and Signal Processing,2015,29(10):1274?1286

119 Liu Y,Chi R H,Hou Z S.Neural network state learning based adaptive terminal ILC for tracking iterationvarying target points.International Journal of Automation and Computing,2015,12(3):266?272

120 Chi R H,Lin N,Zhang R K,Huang B,Feng Y J.Stochastic high-order internal model-based adaptive TILC with random uncertainties in initial states and desired reference points.International Journal of Adaptive Control and Signal Processing,2017,31(5):726?741

121 Chi R H,Huang B,Wang D W,Zhang R K,Feng Y J.Data-driven optimal terminal iterative learning control with initial value dynamic compensation.IET Control Theory&Applications,2016,10(12):1357?1364

122 Chi R H,Liu Y,Hou Z S,Jin S T.Data-driven terminal iterative learning control with high-order learning law for a class of non-linear discrete-time multiple-input-multiple output systems.IET Control Theory&Applications,2015,9(7):1075?1082

123 Chi R H,Liu Y,Hou Z S,Jin S T.High-order datadriven optimal TILC approach for fed-batch processes.The Canadian Journal of Chemical Engineering,2015,93(8):1455?1461

124 Chi R H,Hou Z S.Dual-stage optimal iterative learning control for nonlinear non-affine discrete-time systems.Acta Automatica Sinica,2007,33(10):1061?1065

125 ChiRong-Hu,HouZhong-Sneng,SuiShu-Lin.Nonparameter adaptive iterative learning control for the freeway traffic ramp metering.Control Theory&Applications,2008,25(6):1011?1015(池榮虎,侯忠生,隋樹林.快速路入口匝道的非參數自適應學習控制.控制理論與應用,2008,25(6):1011?1015)

126 Jin S T,Hou Z S,Chi R H,Liu X B.Data-driven model-free adaptive iterative learning control for a class of discrete-time nonlinear systems.Control Theory&Applications,2012,29(8):1001?1009

127 Jin S T,Hou Z S,Chi R H.Optimal terminal iterative learning control for the automatic train stop system.Asian Journal of Control,2015,17(5):1992?1999

128 Janssens P,Pipeleers G,Swevers J.Model-free iterative learning control for LTI systems and experimental validation on a linear motor test setup.In:Proceedings of the 2011 American Control Conference(ACC).San Francisco,CA,USA:IEEE,2011.4287?4292

129 Janssens P,Pipeleers G,Swevers J.A data-driven constrained norm-optimal iterative learning control framework for LTI systems.IEEE Transactions on Control Systems Technology,2013,21(2):546?551

130 Rǎdac M B,Precup R E,Petriu E M,Preitl S,Drago?s C A.Data-driven reference trajectory tracking algorithm and experimental validation.IEEE Transactions on Industrial Informatics,2013,9(4):2327?2336

131 Radac M B,Precup R E.Model-free constrained datadriven iterative reference input tuning algorithm with experimental validation.International Journal of General Systems,2016,45(4):455?476

132 Zhou Y L,Yin Y X,Zhang Q Z,Gan W S.Model-free iterative learning control for repetitive impulsive noise using FFT.In:Proceedings of the 2012 Intentatinal symposium on Neural Networks:Advances in Neural Networks.Berlin,Heidelberg:Springer-Verlag,2012.461?467

133 Wei Q L,Liu D R,Shi G.A novel dual iterativeQ-learning method for optimal battery management in smart residential environments.IEEE Transactions on Industrial Electronics,2015,62(4):2509?2518

134 Radac M B,Precup R E.Optimal behaviour prediction using a primitive-based data-driven model-free iterative learning control approach.Computers in Industry,2015,74:95?109

135 Hou Z S,Chi R H,Gao H J.An overview of dynamiclinearization-based data-driven control and applications.IEEE Transactions on Industrial Electronics,2017,64(5):4076?4090 control,learning control,intelligent traffic systems.Corresponding author of this paper.)