基于知識的污水生化處理過程智能優化方法

喬俊飛 韓改堂 周紅標

水污染是世界上最令人頭疼的問題之一,在未來的幾十年將呈現繼續惡化的趨勢[1].目前,生物處理法是污水處理廠采用最廣泛的凈水方法.其中,活性污泥法是去除有機污染物最有效的方法之一[2].該方法的重要舉措之一就是通過鼓風機向曝氣池中充入適當氧氣以保持好氧區中溶解氧(Dissolved oxygen,SO)濃度以及通過回流泵回流污水以保持缺氧區的硝態氮(Nitrate nitrogen,SNO)濃度,這需要大量的電力能量供給.隨著公眾對環境關注度的提高,出水水質參數的相關標準也越來越嚴格,污水處理廠在“提標改造”過程中不得不使SO和SNO維持于一個較高的運行水平,以便得到滿意的出水水質.然而,好氧區SO濃度過高,有可能破壞反硝化所需的缺氧環境,增大缺氧區可快速降解有機碳的消耗,從而影響污水處理效果.同樣,合適的缺氧區SNO濃度才能保證反硝化反應的順利進行,從而提高脫氮去除率.因此,根據污水處理工況的變化對SO和SNO設定值進行動態尋優,是提升污水處理除氮效果和降低運營成本的一種可行辦法[3].

在實際污水處理廠中,底層跟蹤控制處理過程多采用開關控制和PID控制等傳統控制方法[4?6].Carlsson等[4]設計PI、PD和PID等多種控制策略并集成到BSM1中作為控制性能比較的基準控制器.Wahab等[5]針對硝化反硝化污水處理過程具有的強非線性和不確定干擾等特點,設計了自整定多變量PID控制器,結果顯示閉環控制性能得到極大提高.Harja等[6]針對污水處理過程溶解氧控制設計了分數階PI控制器,結果顯示所設計控制器能夠有效抑制參數變化帶來的控制品質變差的影響,具有較強的魯棒性.雖然傳統控制方法結構簡單易實現,但其初始設置的參數并不能隨時間和工況的變化而動態改變,粗放型的控制過程使得跟蹤誤差較大,并不能很好地控制污水處理過程中包含的非線性動態反應.此外,在實際污水處理運行過程中,其底層設定值往往由廠內專家通過觀察以及經驗決定,由于不能實時監督,導致設定值不能隨時間和工況的變化而改變,因此往往導致能耗過高或者出水水質較差的現象.

針對這一問題,當前一些優化控制技術被應用在污水處理過程中[7?13].Ostace等[7]采用模式搜索算法(Pattern search,PS)優化溶解氧設定值,結果顯示總成本下降7%.Qiao等[8]針對溶解氧和硝態氮的優化控制,采用數據驅動的自適應優化控制器(Data driven adaptive optimization control,DDAOC)優化能耗和出水水質加權和構成的目標函數,結果顯示能耗降低8.5%.韓廣等[9]采用Hop field神經網絡結合拉格朗日乘子法設計污水處理過程優化控制方案,結果顯示總能耗降低5.3%.Santn等[10]采用模型預測控制(Model predictive control,MPC)、前饋控制(Feedforward control,FF)和模糊控制器構建兩層控制器優化溶解氧設定值,結果顯示晴好天氣下總能耗下降6.9%.Zhang等[11]采用遺傳算法獨立地優化操作成本和出水水質,結果顯示在保證出水水質參數達標的同時,有效地降低了操作成本.Sweetapple等[12]針對溫室氣體排放量、生產成本和出水污染物濃度的多目標優化問題,采用非支配排序遺傳算法NSGAII對其進行同時優化以獲取污水處理過程最佳的操作參數,結果顯示在保證出水水質的前提下,溫室氣體排放量和生產成本是一對相互競爭的目標.Hreiz等[13]針對某小型污水處理廠能耗過高的問題,采用精英多目標遺傳算法同時優化出水水質和操作成本,取得了兩者之間的最佳平衡.Qiao等[14]采用模糊神經網絡建立能耗和出水水質數據驅動模型,并利用NSGA-II構建動態多目標優化控制方法(Dynamic multi-objective optimization control,DMOOC)對其同時進行優化,結果顯示能耗降低了4.94%.文獻[7?8]為單目標方法,主要是對溶解氧進行優化控制,優化目標以能耗為主.文獻[9?11]利用權值系數將多目標優化問題轉化為單目標優化問題,并沒有考慮不同目標函數之間的依賴關系.文獻[12?14]考慮到污水處理生化反應過程之間相互影響,能耗和出水水質等多目標之間呈現相互沖突的特性,利用多目標優化算法同時優化多個目標,能夠得到更富競爭力的折衷解.

然而,以上多目標智能優化方法很少應用歷史最優解的信息,對于處理環境相同且最優解決方案變化很小的情況,在新的搜索周期進行完全隨機初始化策略會造成昂貴的計算成本[15].因此,如何在處理新的優化周期時有效應用過去最優解的信息成為當前多目標優化算法的重要課題之一[16].污水處理過程作為非線性動態系統,在相似的處理環境(入水流量、污染物濃度)下具有相近的解決方案,因此應用知識指導優化算法的搜索將能夠得到更精確的優化解.

基于以上多目標優化算法以及污水處理過程特性的分析,本文提出一種基于知識的多目標粒子群(Knowledge-based multi-objective particle swarm optimization,KBMOPSO)優化算法,用于實現污水生化處理過程的智能優化控制.該方法將入水流量(Q0)、入水氨氮(SNH,in)和入水總氮(Stot,in)作為工況識別參考變量,與最優解建立聯系形成知識模型,用于引導KBMOPSO的搜索過程.實驗結果驗證了所提方法的有效性,為污水處理廠提供了切實有效的優化控制方案.

1 問題描述

1.1 過程描述

當前污水處理廠多采用活性污泥法作為處理工藝,其中包含的微生物反應使得處理過程具有非線性和大滯后特性,其工藝布局如圖1所示,圖1中參數定義在表1中給出.污水處理過程由兩部分組成,第1部分為生化反應區,主要通過微生物反應清除污水中含氮污染物;第2部分為二層池,主要通過物理沉降功能實現泥水分離.

1.2 問題分析

圖1所示的污水處理過程在運營過程中存在兩個重要的考察指標,能耗和出水水質.能耗主要包括曝氣能耗和泵送能耗,代表污水處理過程90%的電能消耗.出水水質則直接反映了污水處理過程的好壞.對于一個給定的污水處理過程存在如下特性:1)生化反應的存在以及入水流量和組分濃度的劇烈變化,使得其精確控制極其困難;2)當出水指標超標時需要支付昂貴的罰款,大大提高了污水處理廠的運營成本;3)由于入水的變化,專家需時刻關注污染物的變化從而制定合適的控制變量設定值,需要專家浪費大量的精力才能完成這項任務.

2 污水處理混合智能優化控制系統

圖1 污水處理系統工藝布局圖Fig.1 Wastewater treatment system process layout

表1 參數描述Table 1 Parameters description

為了解決污水處理過程中能耗過大和底層跟蹤控制平穩性較差的問題,本文提出一種基于KBMOPSO的多目標優化控制方法,其控制結構如圖2所示.此系統包含知識庫、多目標優化模塊和底層前饋神經神經網絡(Feedforward neural network,FNN)控制器模塊.

圖2 基于KBMOPSO的多目標優化控制方法Fig.2 Multiple objective optimization control system based on KBMOPSO

在圖2中,y和yr分別代表控制變量實際輸出以及控制變量設定值,C表示知識庫中的案例,e為控制變量設定值與實際輸出值之間的誤差,w,μ和σ分別代表FNN控制器的后件權值、隸屬函數層神經元的中心以及寬度.系統各模塊描述如下:

2)知識庫.知識庫用于存儲歷史非支配解,以Q0,SNH,in和Stot,in作為工況識別參考變量,將參考變量與最優解建立關系形成知識模型存儲在知識庫中,通過判定當前工況與知識庫中歷史非支配解對應工況的相似性,進而在新的優化周期中應用歷史非支配解初始化種群,以引導KBMOPSO的搜索區域.

3)底層控制器.采用FNN設計底層控制器,此控制器充分利用神經網絡的非線性自適應能力,在設定值以及工況發生變化時,迅速調整參數以映射系統變化的輸入輸出關系.

2.1 知識庫的建立與應用

本文提出一種基于知識的MOPSO智能優化搜索算法,如圖3所示.

2.1.1 知識表達

知識表達的一般方法包括屬性特征值描述方法[17]、框架表示方法[18]和面向對象的方法[19]等.由于屬性特征值描述方法具有簡單明了的特點,本文選用其作為知識庫中案例的表達形式,如第k個案例形式可表達為

其中,n表示案例的總數目,Xk和Yk分別表示第k個案例的工況識別參考變量和解決方案(歷史最優解).

圖3 KBMOPSO程序流程圖Fig.3 The program flow chart of KBMOPSO

2.1.2 工況檢索和工況匹配

由于最近鄰法簡單實用,本文利用其結構設計相似工況的搜索算法[20?21].污水處理過程當前工況與知識庫中第k個歷史工況的檢索方程可表示為

其中,sim(xi,xi,k)表示X和Xk之間的相似性,wi表示通過專家經驗獲得的第i個表達屬性的權重值.約束條件定義如下:

若滿足條件

則第k個歷史工況可視為匹配相似工況.其中,wth是分析工況相似程度的閾值.

2.1.3 KBMOPSO種群初始化

如果滿足不等式(4)的案例數目是為m,種群大小為N,則KBMOPSO種群初始化為

步驟1.清除種群P;

步驟2.引用滿足不等式(4)的歷史非支配解作為m個種群初始解;

步驟3.隨機初始化N?m個解;

步驟4.初始化結束.

如果滿足

表明沒有符合條件的歷史工況,則KBMOPSO種群初始化為

步驟1.清除種群P;

步驟2.隨機初始化N個解;

步驟3.初始化結束.

2.1.4 新工況存儲

當式(5)滿足條件時,表明系統出現新的處理工況,如圖3中所示,將KBMOPSO隨機搜索種群初始化后計算得到的最優解作為新工況的解決方案,建立工況識別參考變量與最優解之間關系,形成知識模型存儲在知識庫中.

2.2 多目標優化模塊

多目標優化模塊包括目標函數的建立、多目標優化和Pareto解選取.本文首先建立模糊神經網絡的能耗和出水水質的數據驅動軟測量模型作為目標函數,然后利用多目標粒子群優化算法對目標函數進行優化,最后利用模糊隸屬函數法選取最優折衷解,從而獲得控制變量的優化設定值.在FNN建模中,將入水流量、溶解氧設定值和硝態氮設定值作為輸入量,能耗和出水水質作為輸出量,利用BSM1基準平臺離線產生500組數據,建立軟測量模型.在多目標粒子群優化算法(Multi-objective particle swarm optimization,MOPSO)中,為了能夠提供給決策系統足夠多和足夠好的解,期望算法獲得Pareto前沿盡可能收斂且分布均勻.本文參考文獻[22],利用動態擁擠距離法設計了一個新穎的MOPSO算法.

在MOPSO中,粒子通過不斷調整位置和速度的更新公式來尋找全局最優解,本文所提的MOPSO算法更新公式如下:

其中,t為迭代次數,w為慣性權重,c1,c2和c3為學習因子,r1,r2和r3為[0,1]之間均勻分布的隨機數,pbi和gbi為粒子pi的個體引導者和全局引導者.在式(6)中,通過增加個體引導者和全局引導者之間的隨機擾動提供給粒子更多的位置搜索信息,有助于提高算法跳出局部最優的能力.

在MOPSO中,利用外部檔案(Archive,AC)保存非支配解,通過判斷擁擠距離維護外部檔案.首先將種群中的非支配解加入外部檔案,當外部檔案中的非支配解個數超出設定的容量后,動態刪除擁擠距離小的非支配解.個體引導者的選擇利用Pareto支配關系確定,全局引導者的選擇利用規模為2的錦標賽法決定.最終外部儲備集中的非支配解作為多目標優化模塊的輸出結果提交給決策系統.

本文采用模糊隸屬函數法設計了智能決策系統.對于第i個目標函數Fi,外部儲備集中非支配解xk的滿意度定義如下:

其中,Fmax,i和Fmin,i分別是第i個目標函數Fi的最大值和最小值.非支配解xk的滿意度為

其中,M是目標個數,|Ar|是外部儲備集元素個數.選取μk的最大值對應的解為折衷解.MOPSO算法的偽代碼如下:

算法1.MOPSO算法

2.3 底層控制模塊

由于污水處理過程控制變量設定值頻繁變化,使得底層跟蹤控制過程增加了難度,本文基于模糊神經網絡(Fuzzy neural network,FNN)設計底層控制器,利用梯度下降法在線更新網絡中所含參數,使得控制器的參數可以隨著控制變量設定值的變化而調整,改善了優化控制下的跟蹤控制性能.FNN結構如圖4所示.

圖4 FNN結構圖Fig.4 The structure of FNN

采用S型FNN建立直接自適應控制器,神經網絡輸出為

其中,X=[x1,x2,···,xm]為FNN 的輸入向量,m為輸入變量數,cj=[c1j,c2j,···,cmj]和δj=[δ1j,δ2j,···,δmj]分別為規則層第j個神經元對應的隸屬函數層神經元的高斯函數中心和寬度,φj是規則層第j個神經元歸一化后的輸出,wj為規則層第j個神經元與輸出層神經元之間的連接權,j=1,2,···,n,n為規則層神經元數.

控制量u為

其中,?u(t)=f(X).

FNN的參數學習采用梯度下降算法,定義目標函數為

其中,yd是網絡期望輸出,y為網絡實際輸出.令Θ=[w,c,δ]T表示參數向量,則參數更新公式為

其中,η為FNN參數學習率.

3 實驗結果及分析

3.1 評價指標

實驗基于國際通用仿真平臺BSM1進行,評價指標由BSM1定義的曝氣能耗AE、泵送能耗PE和出水水質EQ組成.具體公式如下:

3.2 參數設置

所有仿真實驗均采用Matlab R2013b編程環境,運行算法的計算機采用四核配置,主頻為2.9GHz.控制器的采樣周期對控制性能有著重要的影響,本文控制器采樣周期為45秒,優化周期為2小時,采用晴好天氣數據進行仿真分析.底層控制器由兩個自適應FNN組成,通過試錯法確定了網絡結構2-6-1,為了保證控制器的穩定性,參數學習率η不宜過大,通過經驗選擇為0.01.

3.3 結果及分析

知識庫中初始案例數為15個,采用區域平均分割生成.實驗數據源于BSM1文件,晴朗天氣共包含14天數據(前7天數據用于訓練,后7天數據用于測試).入水流量和入水組分變化如圖5和圖6所示,圖5顯示入水流量及組分變動比較劇烈.圖6中SS、SNH和SND分別代表入水易生物降解底物、入水氨氮和入水溶性可生物降解有機氮.

案例生成曲線如圖7所示,圖中顯示案例在第7天左右達到41個時已包含所有案例,之后優化時新案例不再增加,這與BSM1對于數據的設置模式相符(前7天數據和后7天數據類似),表明了本文中所提方法關于知識庫案例生成機制設置的合理性.

圖5 晴朗天氣入水流量Fig.5 In fluent flow in dry weather

圖6 晴朗天氣入水組分Fig.6 In fluent component in dry weather

圖7 案例數Fig.7 The case numbers

圖8 和圖9分別給出了能耗和水質的FNN建模效果.從圖8和圖9可以看出,通過數據驅動建立的模型精度較高,可以作為多目標優化算法的目標函數.圖10給出了KBMOPSO與MOPSO在某個優化周期獲得的Pareto解集以及通過智能決策系統選取的最優折衷解.從圖10可以看出,KBMOPSO比MOPSO的收斂性更好,獲取的優化設定值能夠使污水處理過程達到節能降耗的目的.

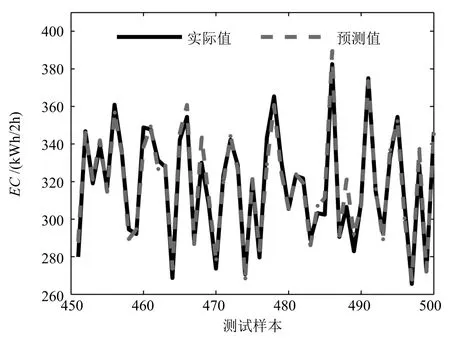
圖8 能耗建模效果Fig.8 Model performance of EC

圖9 出水水質建模效果Fig.9 Model performance of EQ

圖11 和圖12分別給出了設定值優化結果及跟蹤效果和出水水質參數變化情況.由圖11可以看出,KBMOPSO能夠根據處理工況的變化自適應調整優化設定值.優化設定值的調整趨勢與入水流量和入水水質參數的變化一致.同時,利用FNN實現的底層跟蹤控制能夠滿足對控制精度的需求.由圖12可以看出,相比PID恒定值控制,KBMOPSO控制方法出水Ntot明顯降低,出水SNH等都沒有較大變化.KBMOPSO方法的出水水質指標也有一定程度的下降.

圖10 Pareto最優解集及最優折衷解確定Fig.10 Pareto optimal solutions and identify of optimal

圖11 設定值優化結果及跟蹤效果Fig.11 Optimization and tracking results of the set point values

圖12 出水水質參數變化情況Fig.12 The change of water quality parameters

表2 不同算法性能比較Table 2 Performance comparison for different algorithm

表2給出了不同算法之間的性能比較.從表2可以看出,KBMOPSO方法的總能耗為865.9kWh/d,出水水質5092.4kg pollution/d,相比PID恒定值控制,分別下降了6.62%和0.7%.可見,基于KBMOPSO的優化控制方法,可以在不降低出水水質指標的前提下,有效地降低了能耗,節約了運行總成本.

4 結論

針對污水處理過程能耗較大的問題,提出一種基于知識的智能優化控制方法.該方法采用具有案例表達、檢索和修訂等功能的知識模型對MOPSO的搜索過程進行引導,實現了對溶解氧和硝態氮設定值的實時調優,采用模糊神經網絡構建底層控制器,實現污水處理過程的底層精確跟蹤控制.所提方法在實現出水水質達標的前提下,有效地降低了能耗,節約了操作成本.仿真實驗結果也驗證了混合智能優化方法能夠有效降低系統運行總成本,取得了較好的節能效果.

1 Shannon M A,Bohn P W,Elimelech M,Georgiadis J G,Mari?nas B J,Mayes A M.Science and technology for water puri fication in the coming decades.Nature,2008,452(7185):301?310

2 Hamitlon R,Braun B,Dare R,Koopman B,Svoronos S A.Control issues and challenges in wastewater treatment plants.IEEE Control Systems,2006,26(4):63?69

3?Amand L,Carlsson B.Optimal aeration control in a nitrifying activated sludge process.Water Research,2012,46(7):2101?2110

4 Carlsson B,Rehnstrm A.Control of an activated sludge process with nitrogen removal–a benchmark study.Water Science and Technology,2002,45(4?5):135?142

5 Wahab N A,Katebi R,Balderud J.Multivariable PID control design for activated sludge process with nitri fication and denitri fication.Biochemical Engineering Journal,2009,45(3):239?248

6 Harja G,Nascu I,Muresan C,Nascu I.Improvements in dissolved oxygen control of an activated sludge wastewater treatment process.Circuits,Systems,and Signal Processing,2016,35(6):2259?2281

7 Ostace G S,Baeza J A,Guerrero J,Guisasola A,Cristea V M,Agachi P S,Lafuente J.Development and economic assessment of different WWTP control strategies for optimal simultaneous removal of carbon,nitrogen and phosphorus.Computers and Chemical Engineering,2013,53:164?177

8 Qiao J F,Bo Y C,Chai W,Han H G.Adaptive optimal control for a wastewater treatment plant based on a data-driven method.Water Science and Technology,2013,67(10):2314?2320

9 Han Guang,Qiao Jun-Fei,Han Hong-Gui,Chai Wei.Optimal control for wastewater treatment process based on Hopfield neural network.Control and Decision,2014,29(11):2085?2088(韓廣,喬俊飛,韓紅桂,柴偉.基于Hop field神經網絡的污水處理過程優化控制.控制與決策,2014,29(11):2085?2088)

11 Zhang R,Xie W M,Yu H Q,Li W W.Optimizing municipal wastewater treatment plants using an improved multi-objective optimization method.Bioresource Technology,2014,157:161?165

12 Sweetapple C,Fu G T,Butler D.Multi-objective optimisation of wastewater treatment plant control to reduce greenhouse gas emissions.Water Research,2014,55:52?62

13 Hreiz R,Roche N,Benyahia B,Lati fiM A.Multi-objective optimal control of small-size wastewater treatment plants.Chemical Engineering Research and Design,2015,102:345?353

14 Qiao J F,Zhang W.Dynamic multi-objective optimization control for wastewater treatment process.Neural Computing and Applications,2016.1?11,DOI:10.1007/s00521-016-2642-8

15 Mendes R,Rocha I,Pinto J P,Ferreira E C,Rocha M.Differential evolution for the offline and online optimization of fed-batch fermentation processes.Advances in Differential Evolution.Berlin:Springer-Heidelberg,2008.299?317

16 Wang Y,Li B.Investigation of memory-based multiobjective optimization evolutionary algorithm in dynamic environment.In:Proceedings of the 2009 IEEE Congress on Evolutionary Computation.Trondheim,Norway:IEEE,2009.630?637

17 Chai Tian-You.Operational optimization and feedback control for complex industrial processes.Acta Automatica Sinica,2013,39(11):1744?1757(柴天佑.復雜工業過程運行優化與反饋控制.自動化學報,2013,39(11):1744?1757)

18 Porter B W,Bareiss R,Holte R C.Concept learning and heuristic classi fication in weak-theory domains.Arti ficial Intelligence,1990,45(1?2):229?263

19 Cunningham P.A taxonomy of similarity mechanisms for case-based reasoning.IEEE Transactions on Knowledge and Data Engineering,2009,21(11):1532?1543

20 Cover T,Hart P.Nearest neighbor pattern classi fication.IEEE Transactions on Information Theory,1967,13(1):21?27

21 Zhou P,Chai T Y,Wang H.Intelligent optimal-setting control for grinding circuits of mineral processing process.IEEE Transactions on Automation Science and Engineering,2009,6(4):730?743

22 Cheng S X,Zhan H,Shu Z X.An innovative hybrid multiobjective particle swarm optimization with or without constraints handling.Applied Soft Computing,2016,47:370?388