一道高考試題的探源及推論的應用

北京市陳經綸中學 (100020) 張留杰江西省萍鄉中學 (337055) 黃賢鋒

一道高考試題的探源及推論的應用

北京市陳經綸中學 (100020) 張留杰江西省萍鄉中學 (337055) 黃賢鋒

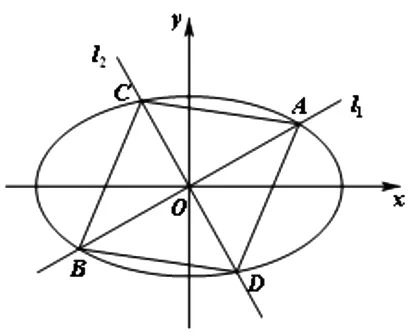
圖1

題目 (2015年上海高考數學第21題)已知橢圓x2+2y2=1，過原點的兩條直線l1和l2分別于橢圓交于A、B和C、D，記得到的平行四邊形ABCD的面積為S(如圖1)．

(1)設A(x1,y1)，C(x2,y2)，用A、C的坐標表示點C到直線l1的距離，并證明S=2|x1y2-x2y1|；

一、試題的根源探究

此高考題讓筆者聯想到北師大版高中數學教材《必修5》第48頁例3，也正是本題的題根所在．我們不妨把它作為本文的定理．

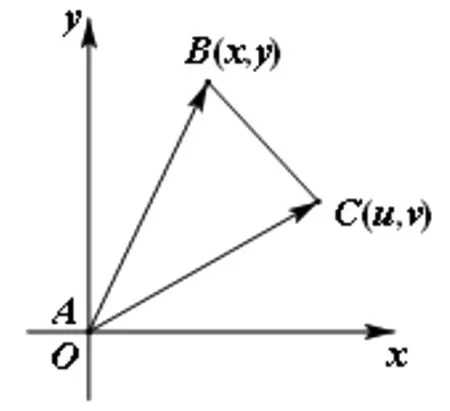
圖2

證明：如圖2，以點A為坐標原點，建立平面直角坐標系，

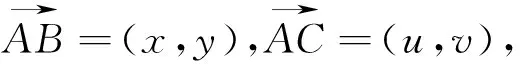
我們可以稱該公式為三角形面積公式的向量形式(坐標形式)，它和三角形面積的行列式形式也是一致的．

能否根據上述三角形面積公式求解任意四邊形的面積呢？經過探究，得出如下推論．

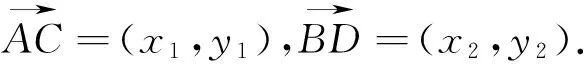
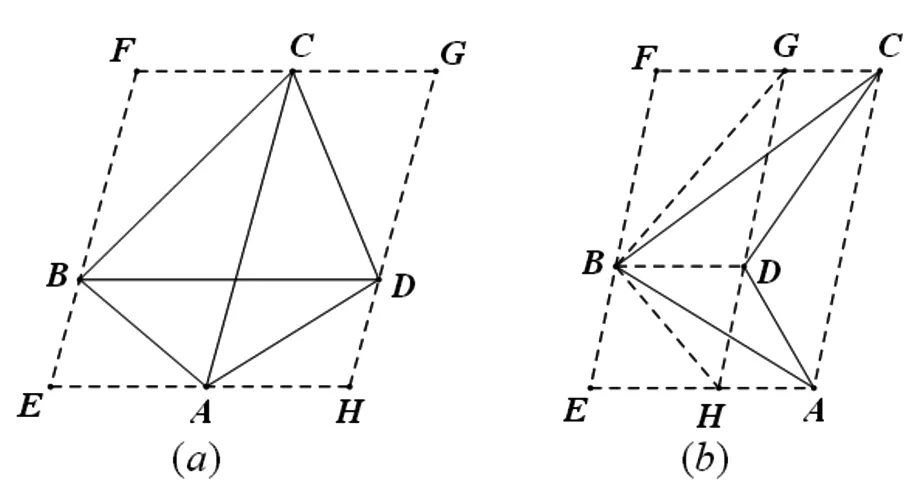
圖3

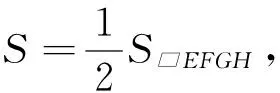
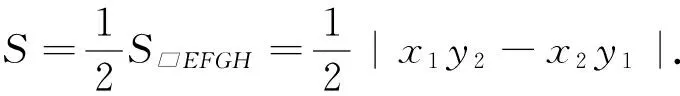
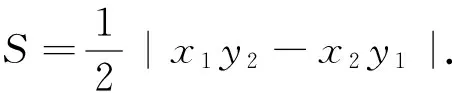
二、推論的應用舉例

本文的推論為解決圓錐曲線中四邊形面積問題提供了一種有力的工具，下面結合兩道高考真題談談它的應用．

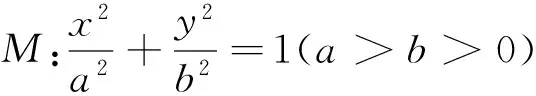
(1)求橢圓M的方程；

(2)C，D為M上的兩點，若四邊形ACBD的對角線CD⊥AB，求四邊形ACBD面積的最大值．

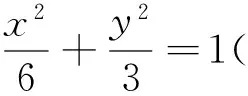
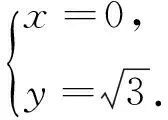
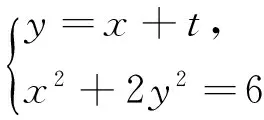
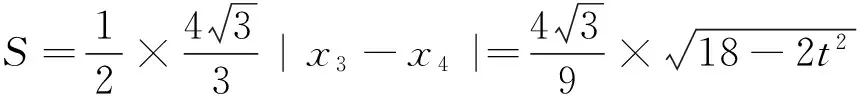
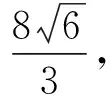
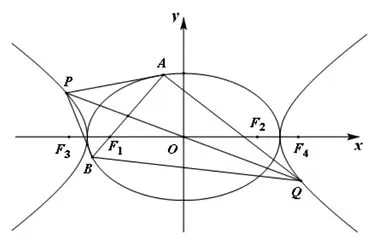
圖4

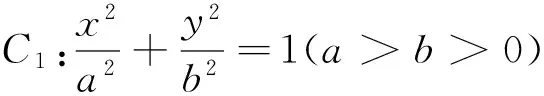
(1)求C1，C2的方程；

(2)過F1作C1的不垂直于y軸的弦AB，M為AB的中點．當直線OM與C2交于P，Q兩點時，求四邊形APBQ面積的最小值．

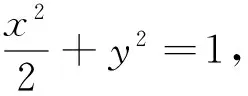
(2)設A(x1,y1)，B(x2,y2)，P(x3,y3)，Q(-x3,

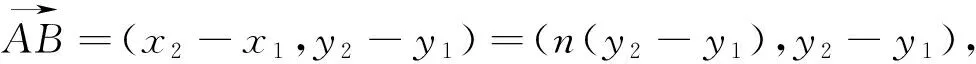
所以當n=0時，Smin=2．故四邊形APBQ面積的最小值為2．