用常數列、零數列證明數列通項公式

貴州省七星關區北大附屬實驗學校 (551700) 魏 星

用常數列、零數列證明數列通項公式

貴州省七星關區北大附屬實驗學校 (551700) 魏 星

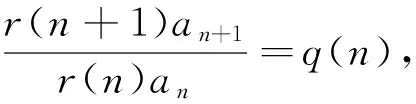
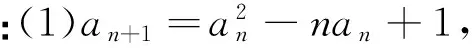
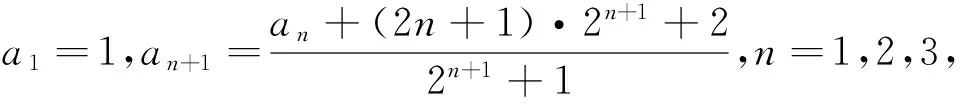
例3 設數列{an}滿足

∵當n=2時，a1-2=0,∴an-(n+1)=0,即an=n+1.

例4 (2014年全國高考廣東卷理19)已知數列{an}的前n項和為Sn，滿足S3=15,Sn=2nan+1-3n2-4n(n∈N*).

(1)求a1,a2,a3；

(2)求{an}的通項公式.

解：由題設，得15=6a4-39，a4=9，n=1得a1=2a2-7，由an=Sn-Sn-1(n≥2)得an=[2nan+1-3n2-4n]-[2(n-1)an-3(n-1)2-4(n-1)](n≥2)，解出

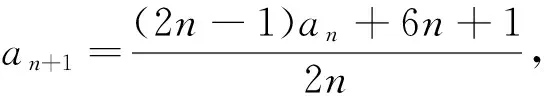
例5 已知數列{an}滿足a1=1，(n+1)an=(n-1)an-1(n≥2,n∈N).求an的一個通項公式.(2016成都市三診理17(1))

總之，一切數列{an}，已知遞推公式an+1=g(an)，求通項公式an=f(n)(可求的話)都可試驗，猜出后，用常數列、零數列證明，即遞推公式an+1=g(an)化為an+1-f(n+1)=h(n,an)[an-f(n)]證明.