第57屆IMO平面幾何題命題賞析

江蘇省南京市鼓樓實驗中學 (210000) 陳 婧

第57屆IMO平面幾何題命題賞析

江蘇省南京市鼓樓實驗中學 (210000) 陳 婧

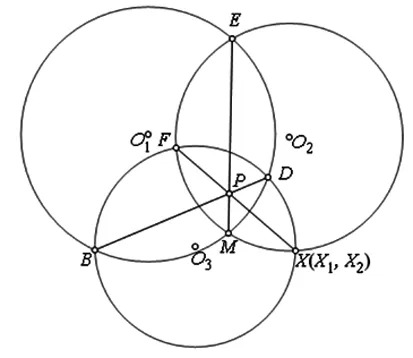
圖1

原題 如圖1，⊙O1與⊙O2相交于E、M兩點，⊙O2與⊙O3相交于F、X兩點，⊙O1與⊙O3相交于D、B兩點，且三圓心O1、O2、O3不在同一條直線上.證明：直線BD、FX、ME三線共點．

證明：令BD與ME相交于點P，連結FP并延長FP，交⊙O2于點X1，交⊙O3于點X2，由相交弦定理，得PF·PX1=PM·PE=PB·PD=PF·PX2，即知PX1=PX2，故X1與X2是同一點，這個點只能是⊙O2與⊙O3的公共點X，于是直線BD、FX、ME三線共點(這點稱為⊙O1、⊙O2、⊙O3的根心)．

這道經典習題實質就是著名的根心定理，此定理是全國高中數學聯賽加試所要考察的重要定理．下面，讓我們來看看這道經典名題是如何被比利時奧賽命題專家巧妙演繹為國際數學奧林匹克(IMO)平面幾何試題的.

先將圖1特殊化：令⊙O1與⊙O2的半徑相等，并且點F、D在連心線O1O2上，點M與圓心O3重合(參見圖2).

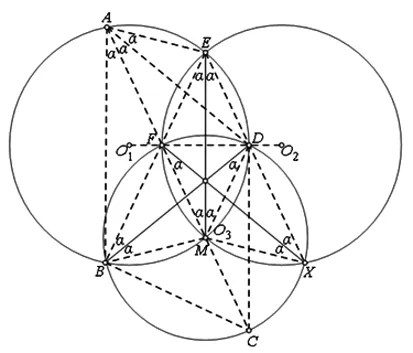
圖2

再將特殊化后的圖2進行演繹：

連結EF、FB、EB、ED、DX、EX、MB、MF、MD、MX，注意到⊙O1與⊙O2是等圓并且分別關于直線FD、ME對稱，知四邊形EFMD是菱形，故∠FEM=∠DEM=∠FME=∠DME．

令∠FEM=∠DEM=∠FME=∠DME=α，注意到點M與圓心O3重合，知∠BEM=∠MDB=∠MBD=∠DEM=∠FEM=α，∠XEM=∠MFX=∠MXF=∠FEM=∠DEM=α，故E、F、B三點共線，E、D、X三點共線．

設直線FM交⊙O1于另一點A，交⊙O3于另一點C，連結AE、AD、AB、BC、CD，即知∠EAD=∠DAC=∠CAB=∠DCA=∠ABE=∠ADE=∠EDA=α，于是AC為∠DAB的平分線，AD為∠EAC的平分線，DA=DC，EA=ED，FA=FB，AC∥ED．

注意到∠EAC=∠XMC=∠DAB=∠DBA=2α，即知DB=DA=DC(點D是ΔABC的外接圓圓心)，AE∥MX，結合AC∥ED，知四邊形AMXE為平行四邊形．

再注意到點M與圓心O3重合，即知M為線段CF的中點，∠FBC=90°(ΔBCF是直角三角形)．

數學競賽的關鍵是命題，而命題的關鍵是創新．

為創建一個陌生且全新的高水準試題，可擦去⊙O1、⊙O2、⊙O3以及線段BM、線段O1O2的痕跡，于是2016年7月在中國香港舉行的第57屆國際數學奧林匹克(IMO)的第1道賽題立即生成：

賽題 在ΔBCF中，∠B為直角．在直線CF上取點A，使得FA=FB，且F在點A和C之間；取點D，使得DA=DC，且AC為∠DAB的平分線；取點E，使得EA=ED，且AD為∠EAC的平分線．設M為線段CF的中點，取點X，使得AMXE為平行四邊形，AM∥EX，AE∥MX．證明：直線BD、FX、ME三線共點．

對于一些經典名題與著名定理，作為參賽選手要能夠熟練應用，而作為參賽選手的教練，不僅要指導學生會靈活運用其解題，還要從三個方面著力思考：一是挖掘經典名題與著名定理的深層內涵嘗試進行命題實踐，二是拓寬與推廣經典名題與著名定理嘗試進行命題實踐，三是向比利時奧賽命題專家學習，對經典名題與著名定理特殊化后不斷演繹，嘗試進行命題實踐．

輔導與命題是教練員的雙翼，缺一不可．

[1]第57屆IMO試題[J].中等數學，2016，8.

[2]熊斌．第57屆IMO試題解答[J].中等數學，2016，9.