WSN中錨節點部署方式對DV—Hop定位精度的研究
謝洪
摘 要:針對WSN中錨節點部署方式對DV-Hop定位所產生的誤差問題進行了研究。通過對錨節點以隨機、正方形、均勻、交叉等不同部署方式對定位誤差所產生的影響進行了仿真、比較和分析,若錨節點以正方形或均勻的方式部署,其對DV-Hop定位所產生的誤差要比隨機部署方式更小。
關鍵詞:無線傳感器網絡;錨節點;部署方式;DV-Hop算法;精度;研究
中圖分類號:TP391 文獻標識碼:A 文章編號:2095-1302(2017)02-00-03
0 引 言
節點位置的信息是無線傳感網絡(Wireless Sensor Network,WSN)能夠實現其應用的關鍵,如何實現節點的準確定位一直是WSN應用中被關注的問題。WSN中的節點主要由錨節點和未知節點組成,其中錨節點指少量帶有GPS定位裝置的節點,能實現精確定位,但未知節點則需要通過錨節點來進行自身定位[1,2]。由于錨節點需加裝GPS設備,能量消耗高,因此無法廣泛使用。
目前WSN中的節點定位分為基于測距(Range-Based)和無需測距(Range-Free)兩種算法[3]。基于測距的算法常用的有RSSI,TOA,TDOA,AOA[4],這種算法需要測算出相鄰節點間的距離,再計算周圍未知節點的坐標,從而實現定位的目的;無需測距的算法主要有DV-Hop算法[5]、質心算法[6]、 APIT算法[7],采用這些算法不需要測出節點之間的實際距離,而是通過估算來獲得未知節點的位置,但估算導致定位存在偏差,需要進一步求精后才能獲取準確位置。
文獻[8]提出把錨節點通過人工部署為小區域的內切圓方式,以提高節點定位的精度。文獻[9]分析了WSN部署與能耗的關系,通過對DV-Hop算法進行研究發現,錨節點位置的不規則放置會對定位誤差產生較大影響,在一定的WSN范圍內使用DV-Hop定位,可以通過錨節點規則性的部署來提高定位的有效性,從而降低傳感器定位誤差。
1 DV-Hop算法及誤差分析
1.1 DV-Hop定位算法
DV-Hop算法的步驟如下:
(1)錨節點向周邊的未知節點廣播信息,信息包中含有初始化為零的最小跳數項。未知節點收到信息包后,對最小跳數項加1再把整個信息包轉發給下一個節點。
(2)錨節點收到其他錨節點的信息和跳數后,按照公式(1)進行計算,估算平均每跳的距離。
1.2 DV-Hop算法誤差
在無線傳感網絡中,對于所有未知節點均使用跳數與校正值的乘積來表示距離,計算出的估計距離與真實距離存在很大偏差。有些文獻提出引用各種迭代算法求出最接近真實值的未知節點的坐標,使得定位誤差最小[10]。但迭代法的引入會增加定位的計算量,并增加WSN的能耗。
存在較大誤差的原因是錨節點位置的不規則放置,導致未知節點離錨很近或很遠,從而加大了估算誤差。
2.2 仿真過程
(1)設定好通信半徑及總節點數,且隨機產生12個錨節點及剩余的未知節點坐標值。
(2)使用DV-Hop算法對每個未知節點進行定位,并計算未知節點的平均定位誤差。
(3)分別使用表2所列的正方形部署、均勻部署、交叉部署坐標代替第(1)步隨機產生的12個錨節點,重復進行第(2)步的運算。
(4)以上(1)~(3)過程重復50次,計算出各未知節點的平均定位誤差。
(5)分別改變通信半徑及總節點數,重新計算第(4)步,得出仿真結果。
3 仿真結果分析
3.1 節點通信半徑對定位精度的影響
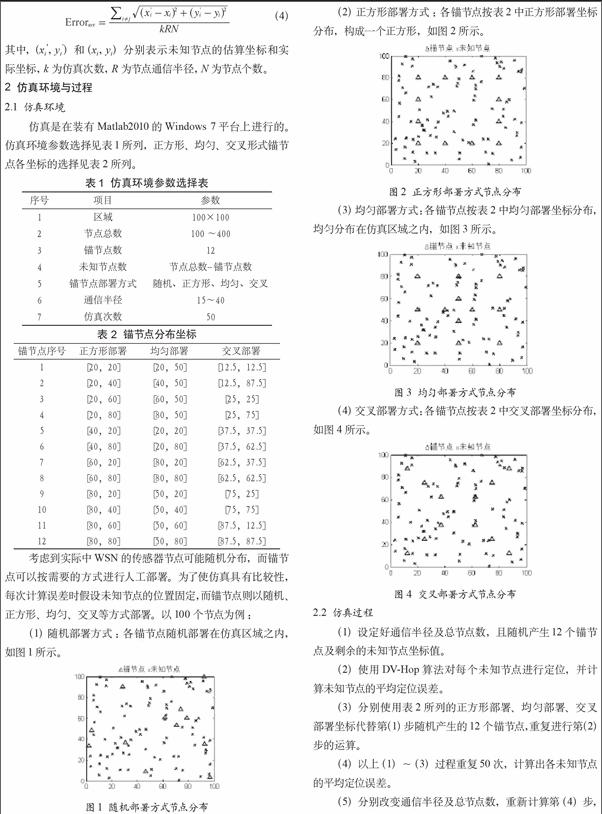
當節點總數為200時,在不同的節點通信半徑下,隨機、正方形、均勻、交叉部署方式對平均定位誤差影響變化曲線如圖5所示。從圖中可以得知:
(1)通信半徑越大,定位誤差越小。
(2)在較小的通信半徑下,以正方形或均勻方式部署,其定位誤差較小,比以隨機部署方式的定位精度更高。
(3)當通信半徑大于整個WSN區域長度的30%時,不同的部署方式將對DV-Hop算法定位誤差產生較小影響。
3.2 節點數量對定位精度的影響
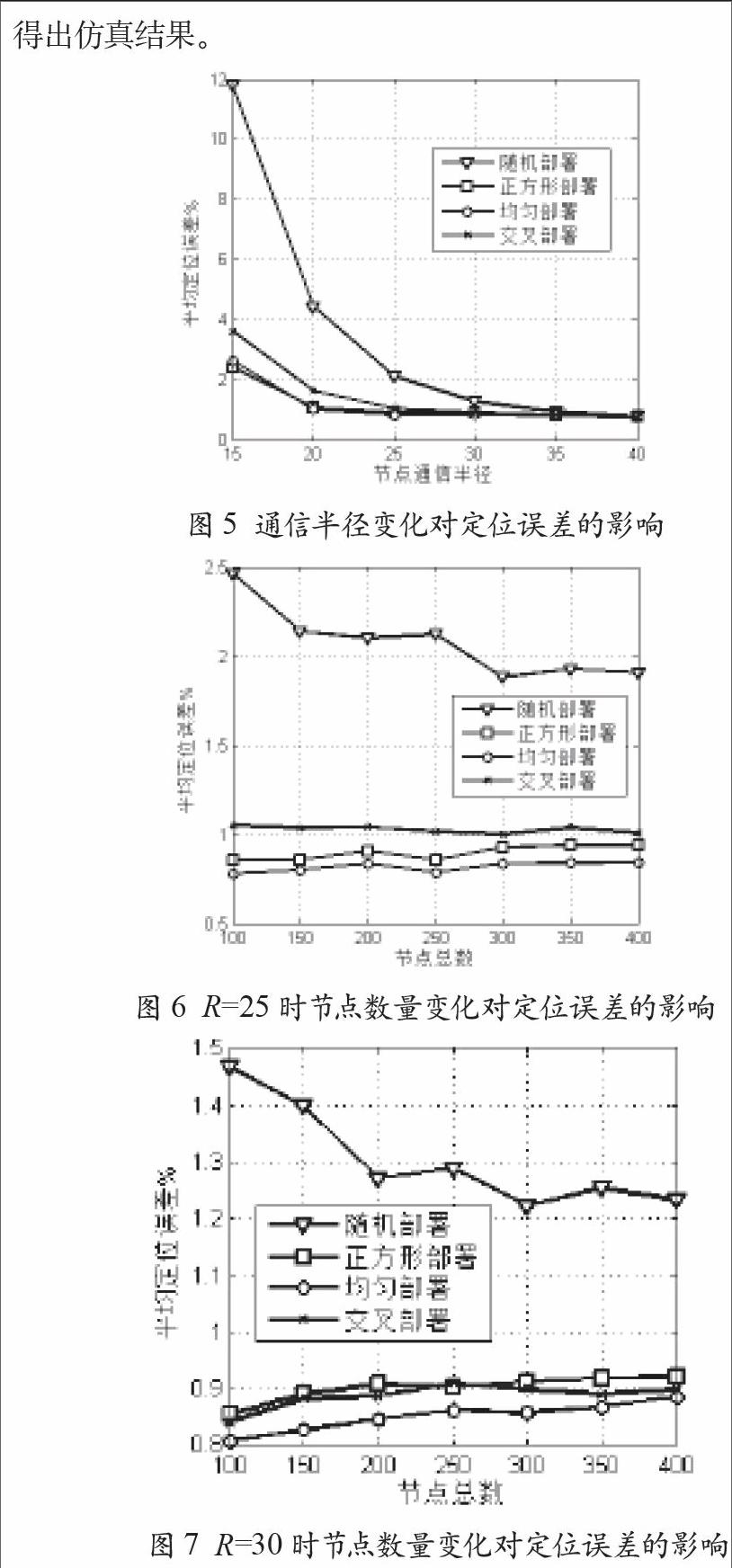
由圖5可知,當通信半徑足夠大時,不同的部署方式對平均誤差影響較小。當通信半徑R=25和R=30時,不同的節點數采用隨機、正方形、均勻、交叉等部署方式,其平均定位誤差變化曲線分別如圖6和圖7所示。從圖6和圖7中可以得知:
(1)以正方形、均勻和交叉等方式部署,其定位誤差要比隨機部署方式更小,而且定位誤差與節點數量關系不大。
(2)采用隨機部署方式時節點數量越多定位誤差越精確。
4 結 語
通過對隨機、正方形、均勻、交叉等不同部署方式對DV-Hop定位所產生的誤差結果進行比較、分析可知,采用正方形、均勻等部署方式能減少定位誤差,有助于改善DV-Hop定位算法的性能。同時,如果通信半徑大于覆蓋范圍的30%時,DV-Hop定位算法的定位誤差更小。文中的研究結果對實際應用具有一定的指導作用。
參考文獻
[1] Akyildiz I,Su W,Sankarasubramaniam Y,et,al.A survey on snesor network[J].IEEE Communications Magazine,2002,40(8):102-144.
[2]王康,王峰,蔣馥珍.基于分跳跳距和粒子群優化算法的DV—Hop定位算法改進[J].計算機測量與控制,2014,22(3):810-812.
[3] Niculescu D,Nath B.DV-based positioning in adhoc network[J].Telecommunication Systems,2003,22(1):267-280
[4]姚汝賢,王曉涓.基于測距和自學習粒子群算法的WSN節點定位[J].重慶師范大學學報(自然科學版),2015,32(1):111-115.
[5]劉杰,董淑福,溫東.一種基于Dv-hop的改進定位算法[J].科學技術與工程,2012,12(24):6059-6063.
[6]嚴雨霞,馮友兵,孫小想.基于移動錨節點的WSN加權質心定位方法研究[J].物聯網技術,2015,5(10):20-22.
[7]吳棟,紀志成,張彪.基于無線傳感器網絡的改進APIT定位算法[J].系統仿真學報,2015,27(12):2965-2972
[8]趙建平,馬淑麗,劉鳳霞,等.WSN中一種新的錨節點分布方式[J].通信技術,2015,48(8):926-933.
[9]胡青松,吳立新,張申,等.煤礦工作面定位WSN的部署與能耗分析[J].中國礦業大學學報,2014,43(2):351-355.
[10]李道全,劉月月,孫付龍.基于DV-Hop的WSN網絡節點定位算法[J].計算機仿真,2014,31(4):303-306.
[11]李牧東,熊偉,郭龍.基于人工蜂群算法的DV-Hop定位改進[J].計算機科學, 2013,40(1):33-36.

