滾動軸承內(nèi)圈局部故障碰撞的Neimark-Sacker分岔研究

賈小權，曲林偉，王 強，劉永葆，趙雄飛，曹平軍，董 瑞

(1.海軍駐哈爾濱七〇三所軍事代表室，哈爾濱 150078； 2.中國船舶重工集團第七〇三研究所，哈爾濱 150078；3.海軍工程大學 動力工程學院，武漢 430030； 4.中國人民解放軍91257部隊，浙江 舟山 316000；5.海軍旅順裝備技術質(zhì)量監(jiān)測站91315部隊，遼寧 旅順 116041)

【機械制造與檢測技術】

滾動軸承內(nèi)圈局部故障碰撞的Neimark-Sacker分岔研究

賈小權1，曲林偉2，王 強3，劉永葆3，趙雄飛1，曹平軍4，董 瑞5

(1.海軍駐哈爾濱七〇三所軍事代表室，哈爾濱 150078； 2.中國船舶重工集團第七〇三研究所，哈爾濱 150078；3.海軍工程大學 動力工程學院，武漢 430030； 4.中國人民解放軍91257部隊，浙江 舟山 316000；5.海軍旅順裝備技術質(zhì)量監(jiān)測站91315部隊，遼寧 旅順 116041)

本文以滾動軸承內(nèi)圈局部故障為研究對象，建立三自由度分段非線性故障碰撞模型，通過在故障缺陷的碰撞面處建立Poincaré映射，研究當故障系統(tǒng)隨頻率增加時，由于滾動體與內(nèi)圈缺陷的碰撞沖擊而出現(xiàn)的Neimark-Sacker分岔等非線性行為，有助于揭示故障碰撞機理，為設備的減振降噪提供理論依據(jù)。

軸承；碰撞；分岔

滾動軸承作為旋轉機構的核心部件之一，廣泛應用在航空飛機、宇宙飛船、火箭、艦船、核反應堆等關系到國計民生的機械設備中，對提高國家的戰(zhàn)略威信、保證人民財產(chǎn)的安全起著舉足輕重的作用，其一旦發(fā)生故障會對設備造成非常嚴重的影響。

目前國內(nèi)外學者對軸承的非線性行為進行了大量的研究，很少從滾動體與軸承內(nèi)外圈缺陷接觸碰撞的角度研究軸承的故障沖擊行為。N.Tandon和A.Choudhury通過假設不同的沖擊信號形狀，如正弦波、矩形波、三角波，分別在軸承故障系統(tǒng)的內(nèi)圈、外圈、滾動體模擬故障，研究了軸承在不同的沖擊信號類型對故障系統(tǒng)的影響，通過對比模擬和實驗數(shù)據(jù)的信號頻率響應說明數(shù)值模擬的準確性[1]；N.Tandon等人把滾動軸承考慮成一個三自由度模型，故障包含內(nèi)外圈滾道的波紋度、尺寸不規(guī)則的滾動體，通過頻譜特性描述其故障特征[2]；N Sawalhi和 R B Randall分析滾動體進出故障位置時的過程，分段研究軸承的振動行為，假設進入故障位置時信號類型為一個階躍沖擊，激起一個更寬頻帶的頻率響應，用倒頻譜分析方法確定其故障位置和故障類型[3]；Alireza Moazenahmadi等人建立了軸承故障非線性動態(tài)模型，假設故障形狀為矩形，研究了故障寬度由小到大時信號的沖擊類型及信號響應[4]；Bai Changqing和Xu Qingyu研究了軸承的徑向間隙和波紋度與軸承非線性行為的關系，發(fā)現(xiàn)軸承徑向間隙和軸向、徑向負載對軸承的穩(wěn)定性具有重要的影響[5]。而國內(nèi)對軸承故障的情況，大多數(shù)作者通常在正常的軸承模型中引入一個周期的脈沖模擬故障，或者引入高頻諧振器模擬高頻故障，或者簡單在損傷處加一個激振力分析非線性故障行為，或者通過假設故障的形狀通過計算彈性形變，在故障位置處施加突增的力模擬故障突變等等[6-9]。國內(nèi)外這些研究都取得了一定的成果，但是這些研究沒有研究由于滾動體的碰撞沖擊對故障系統(tǒng)非線性行為的影響及隨著頻率的增加軸承故障系統(tǒng)可能發(fā)生的非線性行為。本文主要研究單個滾動體與內(nèi)圈缺陷位置碰撞時，由于接觸碰撞導致系統(tǒng)出現(xiàn)的復雜非線性行為，為進一步揭示軸承故障機理提供依據(jù)。

1 滾動軸承內(nèi)圈故障碰撞模型分析

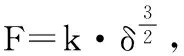
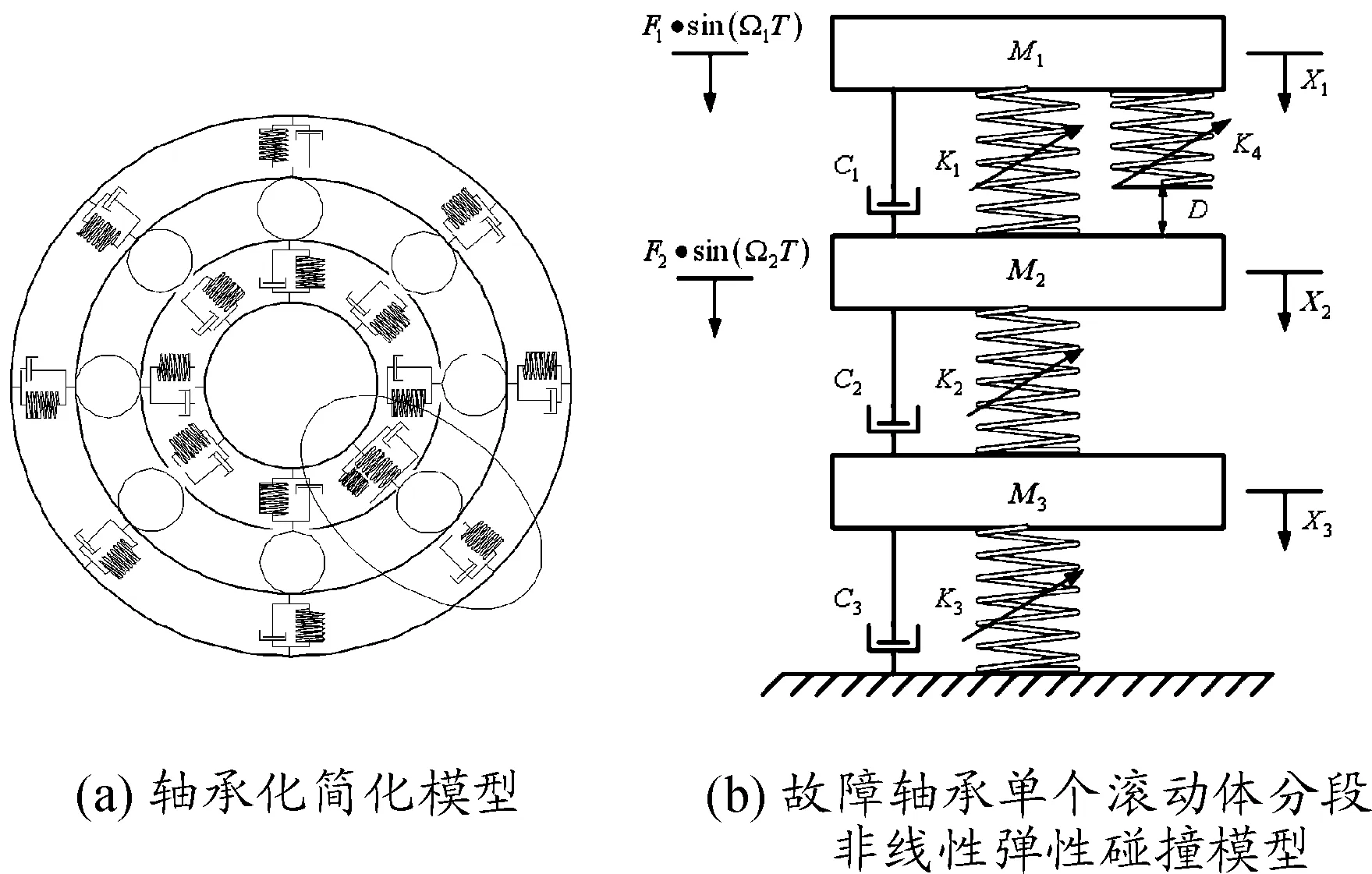
圖1 滾動軸承簡化模型

當滾動軸承正常運轉時，其局部模型運動方程如式(1)。

(1)

在碰撞階段，剛度突然變化，產(chǎn)生碰撞沖擊，系統(tǒng)的運動函數(shù)方程如式(2)。

(2)

為了描述該軸承系統(tǒng)的運動過程，引入一個分界面，以內(nèi)圈故障與滾動體剛接觸時的碰撞面為分界面，如圖1(b)距離滾動體為D的平面。由于碰撞面是隨M1運動的，所以分界面是移動的，首先定義邊界函數(shù)，E=X1-X2-D，分界面可表示如下：

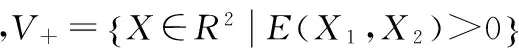
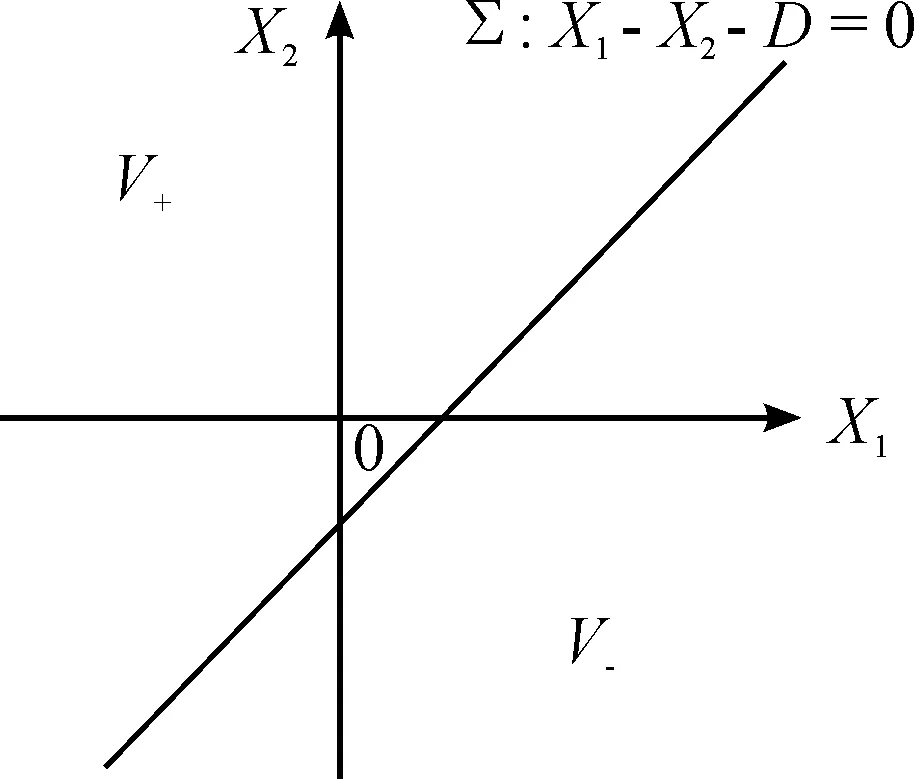
圖2 軸承模型二維相平面圖

在碰撞分界面處取Poincaré截面如下：

其中：θ=ω1t；S=R(mod2π)為1個實數(shù)對2π取余數(shù)。

2 滾動軸承內(nèi)圈故障時Neimark-Sacker分岔數(shù)值仿真研究

當選定其中一組參數(shù)，D=0.002 m，M1=10 kg，M2=1 kg，M3=30 kg，F(xiàn)1=10 N，F(xiàn)2=0 N，C1=0.5 N/(m/s)，C2=0.5 N/(m/s)，C3=0.5 N/(m/s)，K1=1 000 N/m，K2=1 000 N/m，K3=1 000 N/m，K4=2 000 N/m。以滾動體與內(nèi)圈缺陷位置的碰撞面為Poincaré截面，針對質(zhì)塊M1，以外激振頻率為橫坐標，以質(zhì)塊M1的速度為縱坐標，系統(tǒng)的全局分岔圖頻率在4.5～5.5時，如圖3所示。當ω=4.5時質(zhì)塊M1的相圖和Poincaré截面圖如圖4，相圖是單周期，Poincaré界面收斂于一個點。當ω=4.9時質(zhì)塊M1的相圖和Poincaré截面圖如圖5，相圖是一個交錯縱橫的環(huán)面，Poincaré界面收斂于一個圓，說明故障系統(tǒng)此時發(fā)生了Neimark-Sacker分岔。當ω=5.5時質(zhì)塊M1的相圖和Poincaré截面圖如圖6所示，此時故障系統(tǒng)又處于單周期狀態(tài)，相圖是一個圓圈，Poincaré截面收斂于一個點。當ω繼續(xù)增加，ω=7.5時質(zhì)塊M1的相圖和Poincaré截面圖如圖7，相圖出現(xiàn)了周期二的環(huán)帶，其Poincaré界面收斂于兩個圓環(huán)，說明此時發(fā)生了周期二的Neimark-Sacker分岔。隨著頻率增加，當ω=7.7時質(zhì)塊M1的相圖和Poincaré截面圖，如圖8，其相圖變成了周期二的環(huán)帶，其Poincaré界面由兩個圈變成了兩個環(huán)域的奇怪吸引子。故障系統(tǒng)隨著頻率的增加，會出現(xiàn)單周期、Neimark-Sacker分岔、單周期、周期二的Neimark-Sacker分岔、周期二的環(huán)域的奇怪吸引子等復雜的非線性行為過程，轉速的逐步提高會使故障軸承由于碰撞沖擊發(fā)生復雜的非線性行為。

軸承涉及接觸力學、潤滑理論、摩擦學、疲勞與破壞、熱處理與材料組織等基礎研究和交叉學科，而且其本身就是一個非線性的綜合體，該項研究是整體軸承故障研究的重要組成部分，軸承旋轉時，每個滾動體經(jīng)過缺陷位置時都會發(fā)生該頻率狀態(tài)下的碰撞沖擊行為，在下一步的深入研究工作中，建立整體軸承故障模型，將該局部故障系統(tǒng)引入到整體軸承中去，研究多自由度的碰撞接觸，更好的分析軸承故障系統(tǒng)時的非線性行為，為軸承設計提供理論指導，為故障信號特征提取提供一定的依據(jù)。

圖3 系統(tǒng)的全局分岔圖

圖4 ω=4.5時質(zhì)塊M1的相圖和Poincaré截面圖

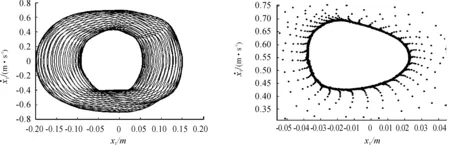
圖5 ω=4.9時質(zhì)塊M1的相圖和Poincaré截面圖

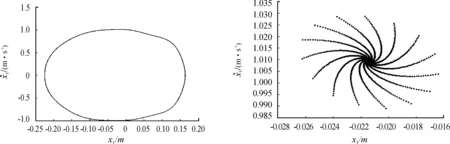
圖6 ω=5.5時質(zhì)塊M1的相圖和Poincaré截面圖

圖7 ω=7.5時質(zhì)塊M1的相圖和Poincaré截面圖

圖8 ω=7.7時質(zhì)塊M1的相圖和Poincaré截面圖

3 結論

本文建立三自由度分段非線性故障碰撞模型，通過在碰撞面建立Poincaré映射，發(fā)現(xiàn)隨著故障系統(tǒng)頻率的增加，故障系統(tǒng)會出現(xiàn)單周期、Neimark-Sacker分岔、單周期再到周期二的Neimark-Sacker分岔，再到周期二環(huán)帶的奇怪吸引子等復雜的非線性行為，說明滾動軸承內(nèi)圈出現(xiàn)故障時，由于滾動體與故障位置碰撞，轉速的增加會使故障系統(tǒng)出現(xiàn)復雜的非線性行為，是軸承整體故障系統(tǒng)研究的重要組成部分，為軸承的設計及設備故障信號的提取提供一定的理論依據(jù)。

致謝：非常感謝海軍工程大學博士生創(chuàng)新基金的資助(XYBJ1502)和國家自然科學基金的資助(51579242)。

[1] TANDON N,CHOUDHURY A.An analytical model for the prediction of the vibration response of rolling element bearings due to a localized deffect[J].Journal of Sound and Vibration,1997,205(3):275-292.

[2] TANDON N,CHOUDHURY A.A theoretical model to predict the vibration response of rolling bearings in a rotor bearing system to distributed defects under radial load[J].Journal of Tribology,2000,122:609-614.

[3] SAWALHI N,RANDALL R B.Vibration response of spalled rolling element bearings:Observations,simulations and signal processing techniques to track the spall size[J].Mechanical Systems and Signal Processing,2011,25:846-870.

[4] ALIREZA MOAZENAHMADI,DICK PETERSEN AND CARL HOWARD.A nonlinear dynamic model of the vibration response of defective rolling element bearings[J].Proceedings of Acoustics,2013,17:1-7.

[5] BAI Changqing,XU Qingyu.Dynamic model of ball bearings with internal clearance and waviness[J].Journal of Sound and Vibration,2006,294:23-48.

[6] 關貞珍,鄭海起,王彥剛,等.滾動軸承局部損傷故障動力學建模及仿真[J].振動、測試與診斷，2012，32(6)：950-956.

[7] 張建軍,王仲生,蘆玉華,等.基于非線性動力學的滾動軸承故障工程建模與分析[J].振動與沖擊,2009,29(11):30-34.

[8] 朱永生,袁幸,張優(yōu)云,等.滾動軸承復合故障振動建模及Lempel-Ziv復雜度評價[J].振動與沖擊，2013，32(16)：23-29.

[9] 曹宏瑞,牛藺楷,何正嘉.高速主軸軸承損傷建模與振動響應仿真研究[J].振動與沖擊，2012，31(S)：241-244.

(責任編輯 周江川)

Neimark-Sacker Bifurcation of Rolling Bearing System with Fault Collision in Inner Ring

JIA Xiao-quan1, QU Lin-wei2, WANG Qiang3, LIU Yong-bao3, ZHAO Xiong-fei1, CAO Ping-jun4, DONG Rui5

(1.The Naval Military Agent’s Room of 703 Research Institute in Harbin, Harbin 150078, China;2. 703 Research Institute of China Shipbuiding Industrial Cooperation, Harbin 150078, China;3.College of Power Engineering, Naval University of Engineering, Wuhan 430030, China; 4.The No. 91257thTroop of PLA, Zhoushan 316000, China; 5.The No. 91315thTroop of Navy Lyushun Equipment Technical Quality Monitoring Stations, Lyushun 116041, China)

Piecewise non-smooth model of three-degree-of-freedom rolling bearing system with fault in inner ring was established by the method of the nonlinear theory. The Neimark-Sacker Bifurcation of bearing system was first studied in this paper. The numerical method was used to further reveal the bifurcations and chaos of bearing system through establishing the Poincaré mapping on the collision plane. With the increase of rotating frequency, the system has experienced the nonlinear dynamical behaviors of classical Neimark-Sacker bifurcations. The study of bifurcation and chaos of the fault bearing system provides reliable basis for the design and fault diagnosis and provides theoretical guidance and technical support for the actual design in the safe and stable operation of large high-speed rotating machinery.

bearing; collision; bifurcation

2016-10-06；

2016-11-05

賈小權(1985—)，男，碩士，工程師，主要從事船舶動力裝置研究。

王強(1985—)，男，博士，工程師，主要從事非線性動力學研究。

10.11809/scbgxb2017.02.028

賈小權，曲林偉，王強，等.滾動軸承內(nèi)圈局部故障碰撞的Neimark-Sacker分岔研究[J].兵器裝備工程學報，2017(2):122-126.

format:JIA Xiao-quan, QU Lin-wei, WANG Qiang,et al.Neimark-Sacker Bifurcation of Rolling Bearing System with Fault Collision in Inner Ring[J].Journal of Ordnance Equipment Engineering,2017(2):122-126.

TH212；TH213.3

A

2096-2304(2017)02-0122-05