例談平面向量中幾種解題技巧
廣東省惠州市第一中學 (516007) 方志平
例談平面向量中幾種解題技巧
廣東省惠州市第一中學 (516007) 方志平
由于平面向量融數、形于一體,它既有一套良好的代數運算法則,又有直觀形象的圖形特征,因而使得平面向量成為研究數與形的一種有效工具,其思想方法獨樹一幟,內涵深邃.又因為平面向量問題的靈活多變,所以很多中學生在學習時覺得困難較大,甚至感到無從下手.基于這些本文借用一些典例淺談平面向量中幾種解題技巧,供同學們學習參考.
1.利用向量的分解與合成解題

A. 直角三角形B. 等腰三角形
C.等腰直角三角形D.等邊三角形

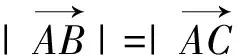

2.引用向量的坐標運算解題
A.13B.15C.19D.21

圖1

點評:這里引用了向量的坐標思想,即用向量的坐標來揭示二維平面上幾何元素的屬性和彼此間的關系,將條件和結論有機的聯系起來.向量的坐標是將幾何問題用代數手段來解決的重要工具,同時,坐標的運用極大地方便了計算和論證.
3.巧用向量的一組基底解題
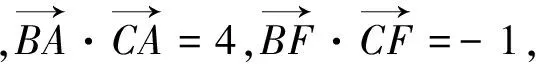
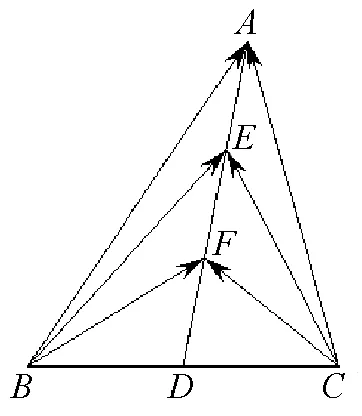
圖2
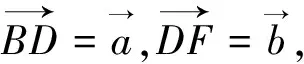
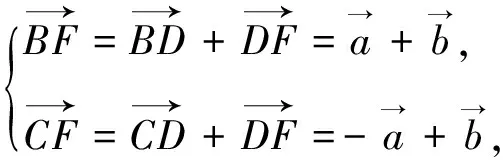
4.使用三點共線解題
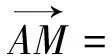


圖3

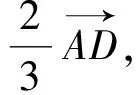
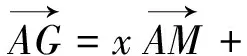
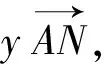
5.妙用向量實數化解題
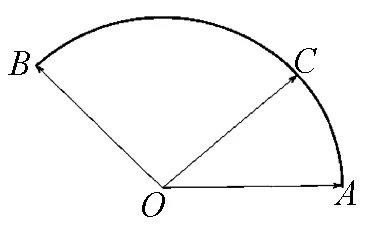
圖4
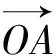
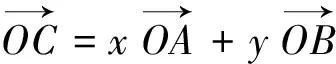
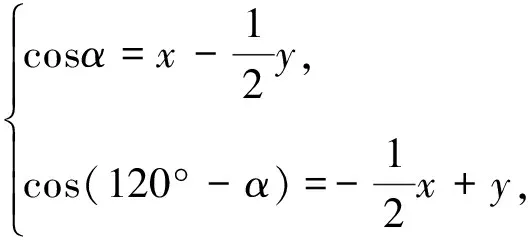
6.構造圖形解題
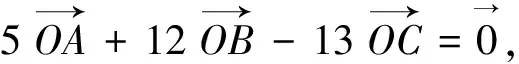

圖5

點評:由于向量兼具代數和幾何的諸多特性,使之成為溝通數與形的樞紐,本題正是根據這一特點,結合題設條件構造特殊圖形進行求解.
7.活用向量的數量積變形公式解題
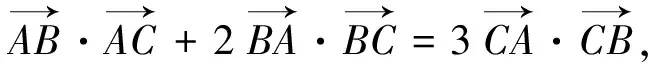

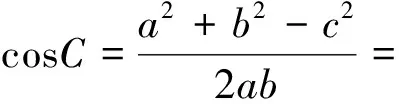
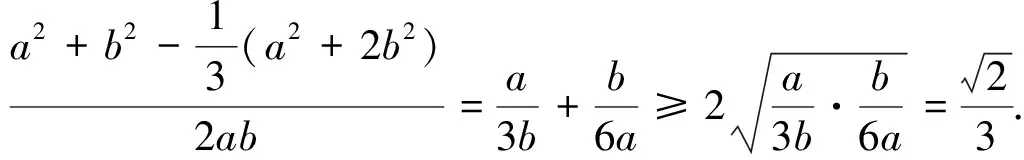
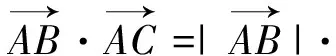
8.運用向量的平行關系解題
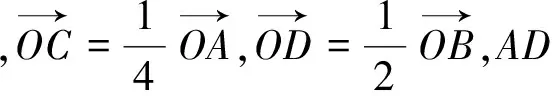
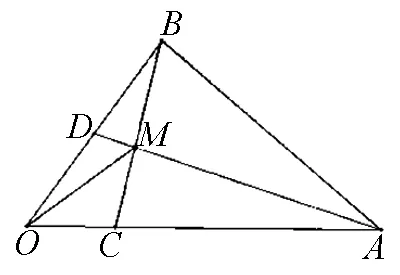
圖6


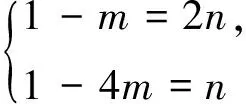
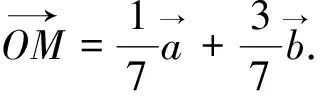
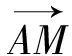
9.采用向量的垂直關系解題
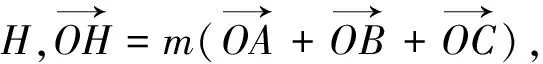
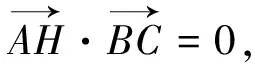

點評:由于本題是一道填空題,故也可使用特殊值法求解,即ΔABC可視為等腰直角三角形,則O是斜邊AB的中點,垂心H是直角頂點.也很容易得出答案.另外,一般處理涉及向量垂直問題的常用方法是利用向量數量積等于零或建立直角坐標系轉化為平面向量的坐標運算.
綜上,平面向量是現代數學中的一個新生內容,它的引入給中學數學帶來了無限的生機,也給中學數學教與學帶來了挑戰.近些年來高中各類考試出現了不少以平面向量為載體的選擇題或填空題,這類問題“小巧玲瓏”,內容豐富,方法靈活,具有一定的綜合性.上述例析的僅是平面向量解題技巧中的冰山一角,本文旨在起拋磚引玉作用,期望讀者能夠觸類旁通.

