數學競賽中的高斯函數

廣東省興寧市寧中中學 (514500) 劉繼東

數學競賽中的高斯函數

廣東省興寧市寧中中學 (514500) 劉繼東

在各級各類的數學競賽中經常出現高斯函數的試題，本文例舉高斯函數在數學競賽中一些應用.

1.解方程

解含[x]的方程，常利用[x]的性質、采用變量代換等方法將方程轉化為不等式，通過解不等式求出原方程的解.

例1 (2015天津)用[x]表示不大于x的最大整數，方程x2-[x]-2=0共有( )個不同的實根.

A.1B.2C.3D.4

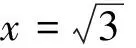
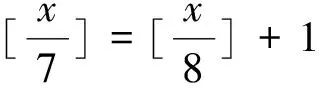
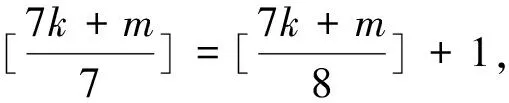
2.求值

[x]的求值問題，可先確定x的取值范圍，再求[x]的值，也可先利用代數變形，再利用高斯函數的性質求值.

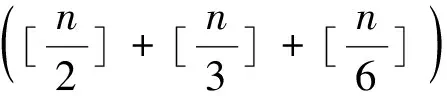
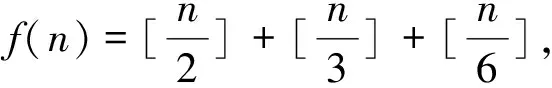
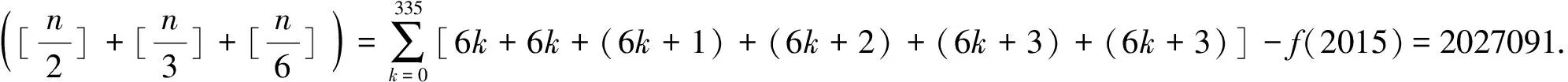
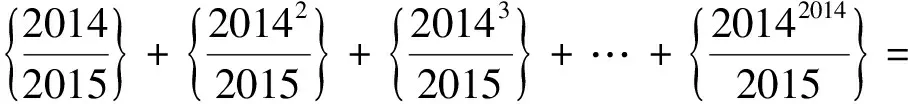
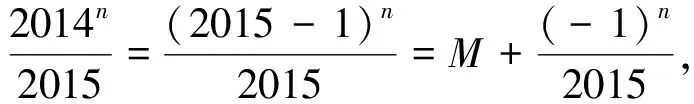
3.平面區域與高斯函數

曲線中含高斯函數，常用方法是分類討論，將曲線分成幾部分來考慮.

例5 (2016浙江)記[x]為不超過x的最大整數.若集合S={(x,y)||[x+y]|+|[x-y]|≤1}，則集合S所表示的平面區域的面積為( ).

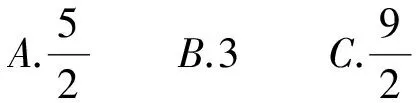
解:當0≤x+y<1時，[x+y]=0，∴|[x-y]|≤1，即-1≤x-y<2；當1≤x+y<2時，[x+y]=1，所以|[x-y]|=0，即0≤x-y<1；當-1≤x+y<0時，[x+y]=-1，所以

|[x-y]|=0，即0≤x-y<1.

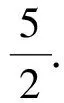
4.數列與高斯函數

數列中的核心問題是求通項與求和，求通項的方法有累加法、累乘法、構造法等，而求和的方法有并項求和、分組轉化、錯位相減、倒序相加、裂項相消等.在解數列與高斯函數這類問題時，這些方法要與高斯函數的定義和性質相結合.

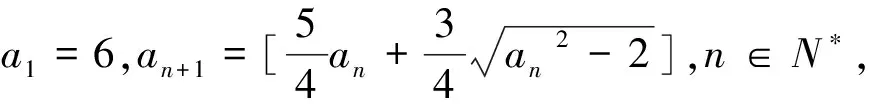
A.1B.2C.5D.6

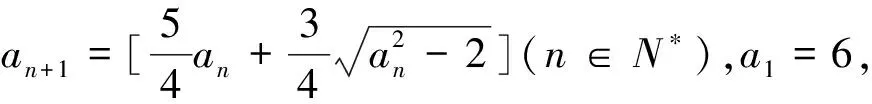
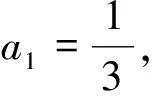
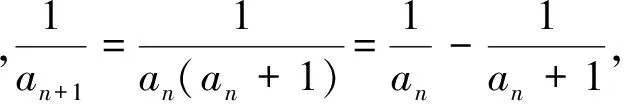
5.個數問題

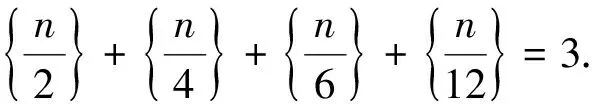
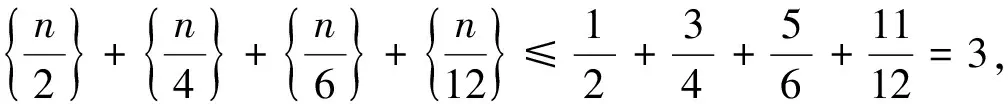
例9 (2016安徽)集合{[x]+[2x]+[3x]|x∈R}∩{1,2,…,100}共有 個元素，其中[x]表示不超過x的最大整數.

解:設f(x)=[x]+[2x]+[3x]，則有f(x+1)=f(x)+6，當0≤x<1時，f(x)的所有可能值為0,1,2,3.由此f(x)值域S={6k,6k+1,6k+2,6k+3|k∈Z}，S∩{1,2,…,100}共有4×17-1=67個元素.

6.同余問題