串聯五個基本三角不等式的一條不等式鏈
2017-03-16 08:42:30福建省福清第三中學350315燈福建省福清東張中學350305王少光
中學數學研究(江西) 2017年2期
福建省福清第三中學 (350315) 何 燈福建省福清東張中學 (350305) 王少光
串聯五個基本三角不等式的一條不等式鏈
福建省福清第三中學 (350315) 何 燈福建省福清東張中學 (350305) 王少光
1.緣起


2.若干引理
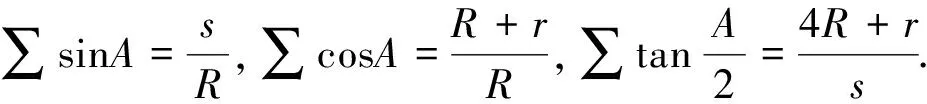
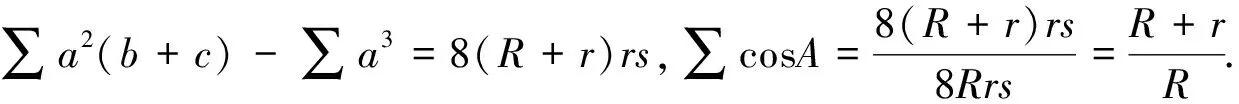

引理2 設ΔABC的三邊為a,b,c,外接圓和內切圓半徑分別為R,r,s為半周長,則有R≥2r(Euler不等式),16Rr-5r2≤s2≤4R2+4Rr+3r2(Gerrestsen不等式).
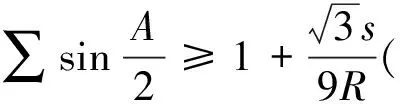
3.一條基本三角不等式鏈
定理 在ΔABC中,有
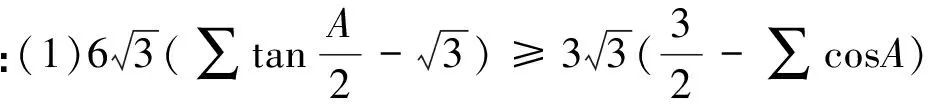


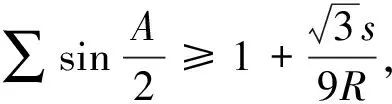
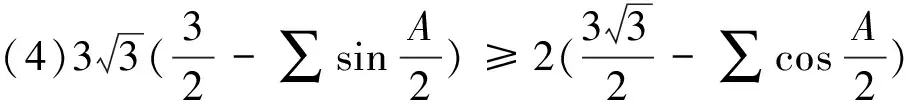
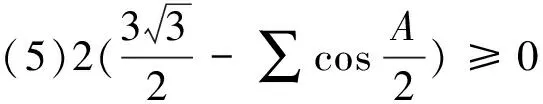
綜上,定理成立.

[1]程漢波.三角代換 巧證代數不等式[J],中學數學研究(廣東),2014(3):38-39.
[2]查正開.一類代數問題的三角解法[J],中學教研(數學),2015(4):15-19.
[3]程漢波.三正數和為1條件不等式的換元證法[J],數學教學,2015(7):27-28.
[4]安振平,崔歧恩.由三角形不等式生成代數不等式的一種方法[J],數學通報,2010(8):48-50.
[5]張俊.一個三角形恒等式繁衍出的代數不等式[J],數學通訊(下半月),2010(9):61-62.
[6]程漢波,楊春波.簡單三角不等式引致的優美代數不等式[J],數學通訊(下半月),2013(3):41-43.
[7]程漢波.再議簡單三角不等式引致的優美代數不等式——從重要三角恒等式的視角[J],數學通訊(下半月),2014(10):52-55.
[8]楊學枝,尹華焱.我國研究三角形中半角三角函數不等式情況綜述[A],楊學枝,不等式研究(第一輯)[C],西藏:西藏人民出版社,2000,6.
[9]安振平.二十六個優美的不等式[J],中學數學教學參考(上旬),2010(1-2):136-143.
猜你喜歡
中學數學雜志(2022年6期)2022-11-18 14:26:15
中學數學雜志(2022年6期)2022-11-18 14:26:15
中學數學雜志(2022年6期)2022-11-17 23:05:58
中學數學雜志(2022年6期)2022-11-14 19:02:07
中學數學雜志(2022年6期)2022-09-05 08:09:54
甘肅教育(2021年10期)2021-11-02 06:14:00
學苑創造·A版(2019年5期)2019-06-17 01:14:21
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21

