基于LH-OAT與變異系數(shù)法的匯流模型參數(shù)敏感性分析

李 昂，祝雪萍，武鵬林

(太原理工大學水利科學與工程學院，山西 太原 030024)

0 引言

流域匯流模型是廣泛應用于洪水預報系統(tǒng)中的預測工具［1］。各地區(qū)根據(jù)本地降雨徑流情況，研制了各種用于洪水預報的匯流模型。但在實際匯流過程中，由于模型結構的簡化和隨機性因素的影響，使得確立模型參數(shù)的工作量加大，模型參數(shù)誤差增加，無法精確評價匯流模型各參數(shù)的重要性及貢獻率，不能保證模型的運行效率和模擬精度。因此，有必要對匯流模型的參數(shù)進行敏感性分析。

目前，多數(shù)流域水文模型參數(shù)敏感性分析多集中在產流模型上，常用的分析方法有擾動分析法、Monte Carlo法、Latin-Hypercube模擬法、隨機OAT法以及LH-OAT等。而關于匯流模型參數(shù)敏感性的分析比較少見，多數(shù)是對參數(shù)的優(yōu)化和改進。周明等［2］對計算瞬時單位線匯流參數(shù)m1公式進行了非線性改進;何書會等［3］以納什瞬時單位線的基本原理為基礎，結合當?shù)貙崪y資料，提出了河北地區(qū)的匯流參數(shù)計算公式;金林［4］運用地貌參數(shù)確定了納什單位線匯流參數(shù)，解決了山西省缺乏地區(qū)匯流資料的問題。

本文以山西省洪水預報系統(tǒng)中的納什瞬時單位線匯流模型為研究對象，通過運用LH-OAT敏感性分析法，對匯流模型中所涉及到的參數(shù)進行敏感性分析，識別模型輸出響應的重要影響參數(shù)，減少了模型參數(shù)率定過程中的盲目性，提高了模型運行的可靠性與預報精度［5］。

1 模型建立

首先，運用GIS對各流域數(shù)字高程模型DEM進行河網(wǎng)提取、子流域劃分，提取各流域植被覆蓋率、河床糙率與河床平均坡度等水文要素，再結合《山西省水文計算手冊》中的匯流參數(shù)取值方法，對山西省洪水預報中的納什瞬時單位線匯流模型參數(shù)進行初始設定，最后運用LH-OAT對流域匯流參數(shù)進行調試。通過分析調試前后模型輸出的洪峰流量、洪水總量的變化，分析匯流模型參數(shù)的敏感性。

山西省洪水預報系統(tǒng)中的納什瞬時單位線匯流模型共有5個匯流參數(shù)，除了參數(shù)C1、C2外，其他參數(shù)均有明確的經(jīng)驗值。根據(jù)LH-OAT敏感性分析法的基本原理，其他參數(shù)不滿足抽樣條件，不需要進行調試，其敏感性不做研究。因此，本文只針對匯流模型參數(shù)C1、C2進行敏感性研究。

2 研究方法

2.1 研究流域概況

分別選用山西省境內飛嶺、固定橋、南莊3個水文站作為研究對象。飛嶺水文站位于山西省安澤縣府城鎮(zhèn)飛嶺村的沁河干流上，控制流域內有3處水位站，14處雨量站;固定橋水文站位于山西省大同縣吉家莊鄉(xiāng)固定橋村西桑干河畔，控制流域內有26處雨量站;南莊水文站位于山西省定襄縣南莊村滹沱河畔，控制流域內有42個雨量站。上述3個流域的研究資料皆來自于多年連續(xù)記錄的降雨量摘錄表、洪水摘錄表、日蒸發(fā)資料。分別選取3個水文站控制流域各5次場次洪水過程，利用標準面積洪峰流量對場次洪水進行等級劃分并進行敏感性研究。各流域概況與洪水信息見表1。

由表1可知，所選場次洪水涵蓋4個等級，一方面可對比分析不同等級洪水下的參數(shù)敏感度;另一方面3個流域的空間尺度、森林覆蓋率、主河床平均糙率與河床平均縱坡各不相同，產生的參數(shù)有一定差異，可對比分析流域特性對匯流模型參數(shù)的影響。

2.2 LH-OAT敏感性分析法

LH-OAT算法是全局敏感性分析法的一種，該算法結合了抽樣法(LH)的健壯性與敏感性方法(OAT)的精確性［6］。具體內容如下:①首先進行LH抽樣，把每個參數(shù)的取值范圍均勻分割為層，將每個參數(shù)按照先前分割的層級，一一對應進行參數(shù)隨機抽樣，每層每次抽一次，則有n個LH抽樣參數(shù)組產生，每個參數(shù)組包含w個參數(shù);②根據(jù)OAT思路，將每個LH抽樣參數(shù)組中的1個參數(shù)進行微小改變，計算目標函數(shù)隨每次微小改變的變化情況［7］;③由LH-OAT算法可知，模型共進行了n(w+1)次運算。多個目標函數(shù)下匯流模型的參數(shù)敏感性計算公式如下

表1 流域概況與洪水過程

式中，O為目標函數(shù)輸出結果;Fi表示模型參數(shù);Ii為參數(shù)Fi在1個LH抽樣集合的相對敏感度;Δ為參數(shù)Fi的定向改變量;Ii為參數(shù)Fi的相對敏感度。

根據(jù)式(1)計算出的相對敏感度大小，可將參數(shù)的敏感性進行分類，分類標準詳見表2。

表2 敏感性分類

以第i場洪水中的洪峰流量Qmi、洪量Wi、過程相對誤差RE、洪量精度評定指標IVF、洪峰誤差PE、模擬流量殘差平方和RSS作為此次匯流模型參數(shù)敏感性分析的目標函數(shù)。計算公式如下

式中，Wi和Wi'為實測和模擬洪量，Qmi和Qmi'為實測和模擬洪峰流量。

2.3 變異系數(shù)法的應用

由上文敘述可知，匯流模型參數(shù)敏感性大小是相對的，不同目標函數(shù)下，其模擬結果是不同的。本文以各有效目標函數(shù)為評價指標，采用變異系數(shù)法，通過權重將多個指標合成1個指標來最終描述敏感性，即通過計算模型參數(shù)的綜合敏感性系數(shù)來最終描述匯流參數(shù)的敏感性，具體計算過程如下:

設有n個評價指標，每個評價指標中有m個指標數(shù)值，則各項指標的標準差為

式中，δj為第j項評價指標的標準差。各項指標的變異系數(shù)為

式中，vj是第j項評價指標的變異系數(shù)。

各項指標在所有評價指標中所占的權重為

式中，wij為第 j項評價指標在所有指標中所占的權重。

3 參數(shù)敏感性分析與討論

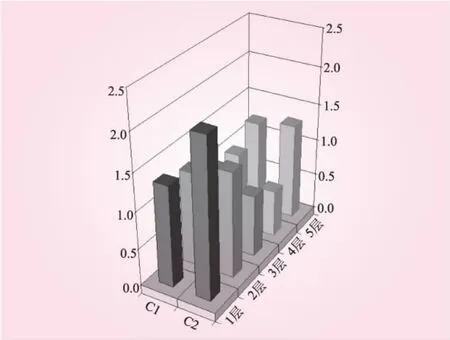
運用LH-OAT法，對納什瞬時單位線匯流模型參數(shù)C1、C2分別在其取值范圍內分成5層進行LH抽樣，抽樣結果見圖1，圖中所示為等比例縮放后的取值。C1為單一地類匯流參數(shù)，取值范圍為1.00～1.357;C2為復合地類匯流參數(shù)，取值范圍為0.580～2.950(在同一種地質、地貌條件下，C2值反映流域植被的好與差［8］);然后對2個參數(shù)運用改進的LHOAT方法分析計算，根據(jù)LH-OAT方法定義，每個流域每場次洪水連續(xù)計算5×(2+1)=15次，計算不同目標函數(shù)下各流域匯流參數(shù)的對應敏感度，計算結果見表3。

由表3可知，目標函數(shù)為 IVF、RE、RSS、Wi的敏感性均為0，視為無效目標函數(shù)，不做分析研究;目標函數(shù)PE和Qmi為有效目標函數(shù)。下面將從不同等級洪水、不同目標函數(shù)、不同流域特性3方面入手，討論分析PE和Qmi對匯流參數(shù)敏感性的影響。

表3 不同流域匯流參數(shù)敏感性系數(shù)

3.1 不同等級洪水的影響

本文計算了飛嶺、固定橋、南莊等3個水文站流域，共15場洪水的模型參數(shù)敏感度，并對比分析了3個流域在不同等級洪水下的敏感度變化情況。下面以南莊水文站控制流域為例，以PE、Qmi為目標函數(shù)，分析不同等級洪水參數(shù)敏感性變化情況。

南莊水文站流域不同等級洪水敏感性見圖2。從圖2可知，在不同等級洪水中，匯流參數(shù)C1、C2的敏感性等級基本上都隨著洪水等級的增大而增大，這說明C1、C2均是對洪峰流量有重要影響的參數(shù)。在不同等級洪水中，各有效目標函數(shù)下，參數(shù)C2的敏感性變化特征均大于參數(shù)C1，這說明參數(shù)C2比參數(shù)C1對洪峰流量的影響更大，相關性也更強，是匯流模型中的重要參數(shù)。

圖2 南莊水文站流域不同等級洪水敏感性

3.2 不同流域的對比研究

對3個流域的匯流模型參數(shù)在相同目標函數(shù)下的敏感度情況進行對比分析，以目標函數(shù)PE、Qmi為例，分析納什瞬時單位線匯流參數(shù)的敏感性變化情況。采用格拉布斯法(Grubbs)進行異常值分析，當定檢水平p取0.01時無異常，置信概率大于99%，數(shù)據(jù)可靠。

橫向來看，參數(shù)C1、C2在同一個流域內均能保持一致的敏感性等級;縱向來看，參數(shù)C1的敏感性等級會隨著不同流域特性的變化而變化，敏感性不穩(wěn)定，參數(shù)C2的敏感性波動性相對較小且敏感性等級較穩(wěn)定，這也反映了不同流域特性的差異及匯流過程中存在的不確定因素對不同地類匯流參數(shù)敏感性的影響。

不同流域中，在敏感性等級相同的情況下，參數(shù)C2的敏感度總是要大于參數(shù)C1。

3.3 不同目標函數(shù)影響

從LH-OAT計算過程可以發(fā)現(xiàn)，匯流模型參數(shù)因模型計算結果的評價目標的不同而改變。

(1)各個匯流參數(shù)對于目標函數(shù)的敏感性整體上表現(xiàn)為C2＞C1。

(2)目標函數(shù)PE、Qmi均為有效目標函數(shù)。在目標函數(shù)PE中，參數(shù)C1、C2均達到了極敏感且C2的敏感性變化更明顯。這體現(xiàn)出不同匯流地類參數(shù)對洪峰流量的影響，復合地類匯流參數(shù)對洪峰流量的影響更顯著。

(3)對目標函數(shù)Qmi而言，隨著洪水等級的不同、流域特性的差異，參數(shù)C1、C2呈現(xiàn)出了一般敏感性到敏感性的變化，不確定性和波動性更大。

3.4 匯流參數(shù)綜合敏感性系數(shù)的確定

應用變異系數(shù)法并結合表3可得匯流模型參數(shù)綜合敏感性系數(shù)，C1、C2綜合敏感性系數(shù)分別為0.42、0.58。參數(shù)C1、C2均為敏感性參數(shù)，且C2＞C1。這基本與每個流域中每場次洪水中計算出的匯流參數(shù)的敏感性相一致，參數(shù)C1、C2均是影響洪水模擬精度的重要參數(shù)，符合山西省小流域洪水預報的實際情況。

4 結語

本文以山西省洪水預報系統(tǒng)中的納什瞬時單位線匯流模型為研究對象，運用LH-OAT法對納什瞬時單位線匯流模型參數(shù)進行抽樣及敏感性分析，結合變異系數(shù)法確定在多目標函數(shù)下匯流模型參數(shù)的綜合敏感性系數(shù)，得出以下結論:

(1)參數(shù)C1、C2是山西省洪水預報系統(tǒng)納什瞬時單位線匯流模型中的重要影響參數(shù)，C2的綜合敏感性系數(shù)大于C1，這與3個研究區(qū)域的敏感性分析結果一致。

(2)運用LH-OAT全局敏感性分析法對山西省洪水預報系統(tǒng)中的納什瞬時單位線匯流模型參數(shù)進行敏感性分析，有效地提高了匯流模型參數(shù)的量化能力，確定了參數(shù)的重要程度，提高了模型模擬精度。

(3)納什瞬時單位線匯流模型參數(shù)的敏感性受不同等級洪水、不同目標函數(shù)、不同流域特性的影響而發(fā)生改變。在實際匯流過程中，為達到更好的模擬效果，應深入了解納什瞬時單位線匯流機理，結合不同地區(qū)的降雨徑流資料及模型的實際運用，識別匯流模型重要的調節(jié)參數(shù)。

［1］孫穎娜．隨機匯流模型及基于隨機理論確定Nash模型參數(shù)的研究［D］．南京:河海大學，2006．

［2］周明，鄧秋良．瞬時單位線匯流參數(shù)m1非線性改進方法探討［J］．湖北水力發(fā)電，2006(1):9-11．

［3］何書會，楊慧英．小流域匯流參數(shù)分析［J］．海河水利，1997(5):15-16，48．

［4］金林．確定Nash模型參數(shù)方法的探討［J］．水資源與水工程學報，2008，19(4):116-118．

［5］CIBIN R， SUDHEER K P， CHAUBEY I．Sensitivity and identifiability of stream flow generation parameters of the SWAT model［J］．Hydrological Processes，2010，24(9):1133-1148．

［6］MCKAY M D，BECKMAN R J，CONOVER W J．A comparison of three methods for selecting value of input variables in the analysis of output from a computer code［J］．Technometrics，1979，21(2):239-245．

［7］徐會軍，陳洋波，李晝陽，等．基于LH-OAT分布式水文模型參數(shù)敏感性分析［J］．人民長江，2012，43(7):19-23．

［8］張澤宇，張永愛，梁存鋒．流域水文模型在臨界雨量分析中的應用研究［J］．人民黃河，2015，37(1):38-41．