基于小波變換的徑流與降水時頻變化及相關性分析
----以五郎河為例

陳一明，何子杰，賁 月，董慶華

(1.長江勘測規劃設計研究院，武漢 430010；2.武漢大學水資源與水電工程科學國家重點實驗室，武漢 430072)

五郎河屬金沙江一級支流，是金沙江上游一條重要支流，具有豐富的水能資源，地跨麗江市寧蒗、永勝兩縣。隨著麗江市旅游業迅速發展，永勝縣供大于求的用水矛盾以及程海水生態環境惡化的問題日益凸顯。因此，探討五郎河流域徑流的變化規律及影響因素，不僅可為該流域水資源的開發利用提供重要的參考依據，而且對當地生態環境保護、生態環境建設具有重要指導意義。

徑流和降水是水文循環的基本要素，其變化均具有復雜的隨機性和不確定性，而降水又是影響徑流的水文氣象因素之一，因此對徑流變化的規律和特點的描述及其影響因素的相關性探尋一直是水文領域研究的重點。小波變換是在窗口傅里葉變換的基礎上發展起來的，是一種分析信號的新方法[1]，其良好的時-頻局部性及多分辨率特點使其廣泛應用于水文領域，尤其是對非平穩的水文時間序列的分析[2,3]。而徑流與降水均是非平穩卻又能呈現一定的周期變化的時間序列，因此運用小波變換對它們的時-頻變化進行多尺度分析，可以得到徑流與降水時間序列主要尺度以及各尺度下的“豐-枯”和“多-少”變化過程，從而可預測它們在各尺度下的變化趨勢。

交叉小波分析是一種將小波功率譜與交叉譜結合起來的一種新方法[4-6]，該方法可以對兩個非平穩時間序列間的相關程度進行有效分析，能夠揭示兩者在特定時間尺度和頻域上的相位關系，從而能更深層地理解兩個時間序列間互相關關系。

本文基于五郎河流域主要測站實測徑流資料及麗江氣象站降水資料，采用Morlet小波變換法，分別對五郎河56年(1959-2014年)以來年徑流量以及麗江同時間段(1959-2014年)的年降水的變化特性及其變化規律進行分析，并運用交叉小波分析方法，對徑流和降水在時域和頻域中的多尺度相關性及其周期性進行分析，與傳統的方法相比，能夠更精確地評估五郎河徑流變化趨勢以及降水對徑流的影響，為更好地開發利用五郎河流域水資源提供了理論基礎。

1 研究區域

五郎河系金沙江的一級支流，地跨麗江市寧蒗、永勝兩縣，河長約為98.1 km，落差2 270 m，經戰河鄉、西布河鄉后，橫穿永勝縣北部，在永勝縣太安鄉匯入金沙江干流。五郎河流域面積2 088 km2，分水嶺高程一般在3 000 m以上，上游穿行于峽谷之中，水流湍急；支流呈扇形分布；下游兩岸地形開闊，為三川盆地(圖1)。

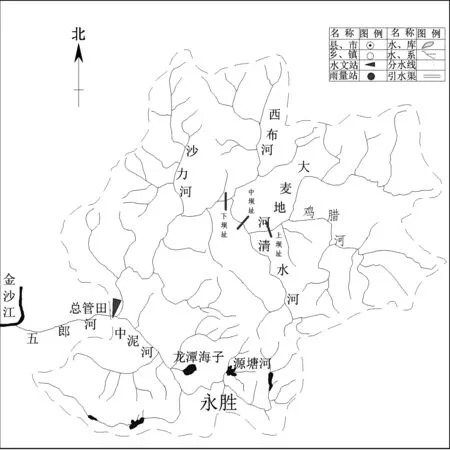
圖1 五郎河流域水系圖Fig.1 Wulang River Basin

五郎河流域屬橫斷山系的高山峽谷區，河流兩岸陡峭險峻，呈“V”字形。該流域屬于暖溫帶季風氣候，干濕季分明，夏秋多雨，冬春多旱，霜期較長，濕度大，多年平均相對濕度為69%，流域東西差異較大，氣候垂直變化顯著，河谷地帶地勢較低，氣溫較高，降水較少，屬中亞熱帶或南亞熱帶氣候。流域內多年平均氣溫為13.7 ℃，多年平均降水量為951 mm。

2 研究方法和數據來源

2.1 小波變換

小波變換是通過將時間序列分解到時域和頻率域內，從而得出時間序列的顯著的波動模式，即周期變化，以及周期變化的時間格局。小波變換分為連續小波變換(Continuous Wavelet Transform, CWT)和離散小波變換(Discrete Wavelet Transform, DWT)，DWT是數據的緊湊表示，常用于降噪與數據壓縮處理；而CWT適用于信號特征的提取[4]。由CWT變化的結果得到的小波系數表示時間序列與小波的近似程度。目前，Morlet小波函數因其與徑流、降水、氣溫等時間序列的波形相似，且可以探測時間序列在不同頻域中時域的振幅和相位，極好的表現出時-頻域的局部特征的優勢[7,8]，被廣泛應用于水文氣象時間序列中[9,10]。因此，本文采用Morlet復值小波對徑流和降水時間序列進行小波變換。小波變換及Morlet小波變換理論具體方法詳情參見文獻[4,7,8,11]。

2.2 交叉小波變換

將小波變換與交叉譜分析相結合的方法稱之為交叉小波變換，它是一種可以從多尺度來分析兩個時間序列在不同時域和頻域中的相互作用顯著性的新方法[12]。在兩個時間序列的連續小波譜的基礎上，構造兩者的交叉小波譜(Cross Wavelet Transform, WTC)，可以反映兩個時間序列的在不同時頻域上所具有相同或相近能量譜區域的范圍，該能量譜值越大，表示兩時間序列在不同時頻域上相互作用的越顯著。

為了更好地研究兩個水文序列之間的相關關系，引入小波相干譜(Wavelet Coherence,WC)或凝聚譜，旨在揭示兩個時間序列間互相關性對頻域的依賴程度。具體交叉小波譜及小波相干譜理論方法參見文獻[5,7,12-14]。

2.3 數據來源

由于總管田水文站為五郎河流域的控制站，因此本研究以總管田水文站為主，收集了總管田水文站的實測徑流資料(1959-2014年)。麗江氣象站降水資料(1959-2014年)來源中國氣象數據網(http://data.cma.cn/)。為了避免徑流和降水時間序列中極端天氣變化誤差的干擾，運用SPSS統計分析軟件，分別對年徑流量和年降水量統計數據進行標準化處理。

3 結果分析

3.1 周期變化特性分析

通過Morlet復值小波方法分別對總管田水文站和麗江氣象站56 a(1959-2014年)標準化年徑流序列和降水序列進行連續小波變換，分析小波變換系數的實部、模平方、方差等信息，揭示年徑流變化和年降水的多時間尺度變化規律。

3.1.1 小波系數實部時頻分析

小波系數實部可以反映時間序列在不同時間尺度下的周期變化及其在時間域中的分布情況，進而可以判斷在不同時間尺度上，時間序列的未來變化趨勢[15-19]。

圖2(a)和2(c)為標準化年徑流和年降水序列小波系數實部等值線圖。小波系數實部大于0時，表示徑流量偏豐[圖2(a)和2(c)中深色區域]；相應地，若小波系數實部小于0時，表示徑流量偏枯[圖2(a)和2(c)中淺色區域]；而小波系數等于0時，則表示徑流處于平水期。圖2(a)和2(c)均呈現出明顯的年際變化(10年以下)和年代際(10年以上)變化，即從大尺度至小尺度(縱坐標由上至下)來看：

(1)對于徑流[圖2(a)]，存在2種尺度的周期變化：6～28 a和2～5 a，這兩種尺度下豐、枯交替變化較明顯，貫穿整個時間序列，而30 a以上的尺度并未看到明顯的周期變化。從大尺度6～28 a來看，徑流隨著時間序列變化(橫坐標由左至右)表現出了“枯-豐”交替的準兩次震蕩，存在明顯的突變特性，具體表現為1959-1964年偏枯，1968-1976年偏豐，1984-1998年偏枯、2002-2014年偏豐，整個尺度的周期變化在整個時間序列中的狀態很穩定，占據了整個時間序列，具有全域性；而小尺度2～5 a的周期變化，主要在1960s-2000s表現得較為活躍，存在“枯-豐-枯”的周期變化。

(2)對于降水[圖2(c)]，存在3種尺度的周期變化：16～28 a、9～14 a和4～8 a，其中16～28 a、4～8 a尺度的多-少交替變化表現較明顯，貫穿整個時間序列，而30 a以上的尺度除了局部包含在16～28 a的閉合范圍內之外，其余也并未看出明顯的周期變化。從大尺度16～28 a分析，降水量出現“少-多”交替的準5次震蕩，突變特性明顯，且從圖2(c)中可以觀察到，在整個時間序列中振蕩最強的時間尺度均出現在這一范圍內，表現很穩定，說明該尺度在整個時間序列中具有全域性；9～14 a的周期變化主要在1960s-1990s表現較活躍，降水量出現“多-少”交替的準4次振蕩；而小尺度4～8 a的周期變化，存在“少-多-少”周期變換。

比較圖2(a)和2(c)可知，盡管徑流和降水的周期變化并不十分一致，但兩者存在全部包含和部分包含的關系，如徑流的大尺度6～28 a是包含了降水的16～28 a和9～14 a，但徑流的小尺度2～5 a與降水的4～8 a只是部分包含的關系。此外，從圖2(a)和圖2(c)中還可以發現，無論是徑流還是降水，均存在若干小尺度下的豐-枯期(多雨-少雨期)嵌套在一個大尺度下的偏豐期(多雨期)或者偏枯期(少雨期)的現象，小尺度下的突變點要比大尺度多，且各時間尺度下的突變點個數及其所在的時間位點均不同，因此應在具體時間尺度研究突變點。

3.1.2 小波能量多尺度特征

小波系數的模平方即為小波能量譜，可以分析時間序列在不同周期下的振蕩能量。圖2(b)和2(d)分別為標準化年徑流和年降水序列小波系數等值線模平方圖。

(1)年徑流：從圖2(b)可以觀察到，在整個徑流時間序列中8～18 a時間尺度能量最強，表現出的周期性最明顯，其中心點對應11～12 a。但它的周期變化具有局限性(1999年后)；2～5 a尺度的周期振蕩強度次之，其他時間尺度的周期變化不明顯。這一分析結果與上文分析的6～28 a和2～5 a周期變化基本一致。

(2)年降水：從圖2(d)中可以看出，在整個降水時間序列中表現出的能量最強、周期性最明顯的時間尺度為16～24 a，且其中心點不唯一，分布在1960-1974年間和1990-1995年間，同樣，它的周期變化也具有局限性(2009年前)；8～12 a和4～7 a尺度的周期振蕩強度次之，其他時間尺度的周期性變化不明顯。顯然，這一結果與上文所分析的16～28 a、9～14 a和4～8 a周期變化基本一致。

比較圖2(b)和2(d)可知，盡管年徑流與年降水周期最明顯的時間尺度不一致，但從整體來看，兩者的周期變化基本一致；兩者的周期變換均具有局限性，年徑流表現更明顯。

3.1.3 小波方差檢驗主周期

小波方差圖是刻畫的是小波方差隨時間尺度的變化過程，可以找出水文時間序列在其形成過程中所存在的主周期[11]。圖3(a)和3(c)分別為年徑流和年降水小波方差圖。

可以看出，圖3(a)中存在2個峰值，從左至右分別對應3 a和12 a時間尺度，其中，12 a左右的周期振幅最大，為此徑流序列變化的第一主周期，則3 a為次主周期；而圖3(c)中明顯看到有4個峰值，從左至右分別對應4、6、18和26 a時間尺度，其中，18 a左右的周期振蕩最強，為此降水序列變化的第一主周期，則4 a和6 a分別為第二、第三主周期。兩者的分析結果均分別在小波能量譜的分析結果范圍內。

3.1.4 不同周期尺度的豐-枯(多-少)變化分析

基于小波方差檢驗的結果，選擇振蕩較強的主周期繪制相應尺度下的小波系數實部圖，分析不同時間尺度下，水文時間序列的平均周期及其豐-枯(多-少)變化規律。圖3(b)和圖3(d)分別為年徑流和年降水在主周期尺度下的小波變換實部圖。圖中，小波變換實部>0時代表流量較大，實部<0時表示流量較小，不同尺度對應不同的豐-枯(多-少)變化。

(1)年徑流：從圖3(b)可知，在12 a時間尺度下，徑流序列經歷約1.5個波動周期，徑流豐枯的突變點在1964-1965(枯-豐)、1980-1981(豐-枯)，1997-1998(枯-豐)，2007年處于該尺度下的偏豐階段的波動極大值處。從變化趨勢可以預測2014年后徑流的變化趨勢為逐漸減少，同時，還可以預測在12 a時間尺度(2022年前后)徑流將由枯變豐；在3 a時間尺度下，徑流豐枯的突變點在1965-1966(枯-豐)、1970-1971(豐-枯)、1973-1974(枯-豐)，1977-1978(豐-枯)，1979-1980(枯-豐)，1982-1983(豐-枯)，1986-1987(枯-豐)，1987-1988(豐-枯)，1990-1991(枯-豐)，1994-1995(豐-枯)，2000-2001(枯-豐)，2012-2013(豐-枯)，同樣，從變化趨勢可以預測2014年以后徑流有減少的趨勢，且在3 a時間尺度(2018年左右)徑流將由枯轉豐。

(2)年降水：從圖4(d)可知，在18年時間尺度下，降水序列經歷約3個波動周期，其變化的平均周期約為18 a；降水量豐枯的突變點在1962-1963(少-多)、1968-1969(多-少)，1974-1975(少-多)，1980-1981(多-少)，1986-1987(少-多)，1992-1993(多-少)，1998-1999(少-多)，2003-2004(多-少)，2009-2010(少-多)。從變化趨勢可以預測2014年后徑流的變化趨勢將逐漸減少，同時，還可以預測在18 a時間尺度(2024年左右)降水量將由少變多。在6 a和4 a時間尺度下，降水序列分別經歷9個和9.5個周期波動，其變化的平均周期分別約為6 a和5.9 a。從變化趨勢來看，6 a時間尺度下，預測2014年以后降水量有增加的趨勢，且在2017年左右降水量由多雨期轉為少雨期，而4 a時間尺度下，預測2014年以后降水量有減少的趨勢，且在2016年降水量由少雨期轉多雨期。

比較分析圖4(b)和圖4(d)可知，年徑流在各尺度下的平均周期均比年降水要大，而從兩者的第一主周期來說，其預測2014年后徑流和降水均有減少的趨勢，但仍然處于豐水(多雨)期，分別在8 a和10 a后由豐(多)轉枯(少)。此外，由兩圖可以看出，小尺度的豐-枯(多-少)交替變化是嵌套在大尺度的豐-枯(多-少)結構中，即大尺度為豐(多)時，對應的小尺度可能是枯(少)，反之，亦然。這與3.1.1節的分析結果一致。

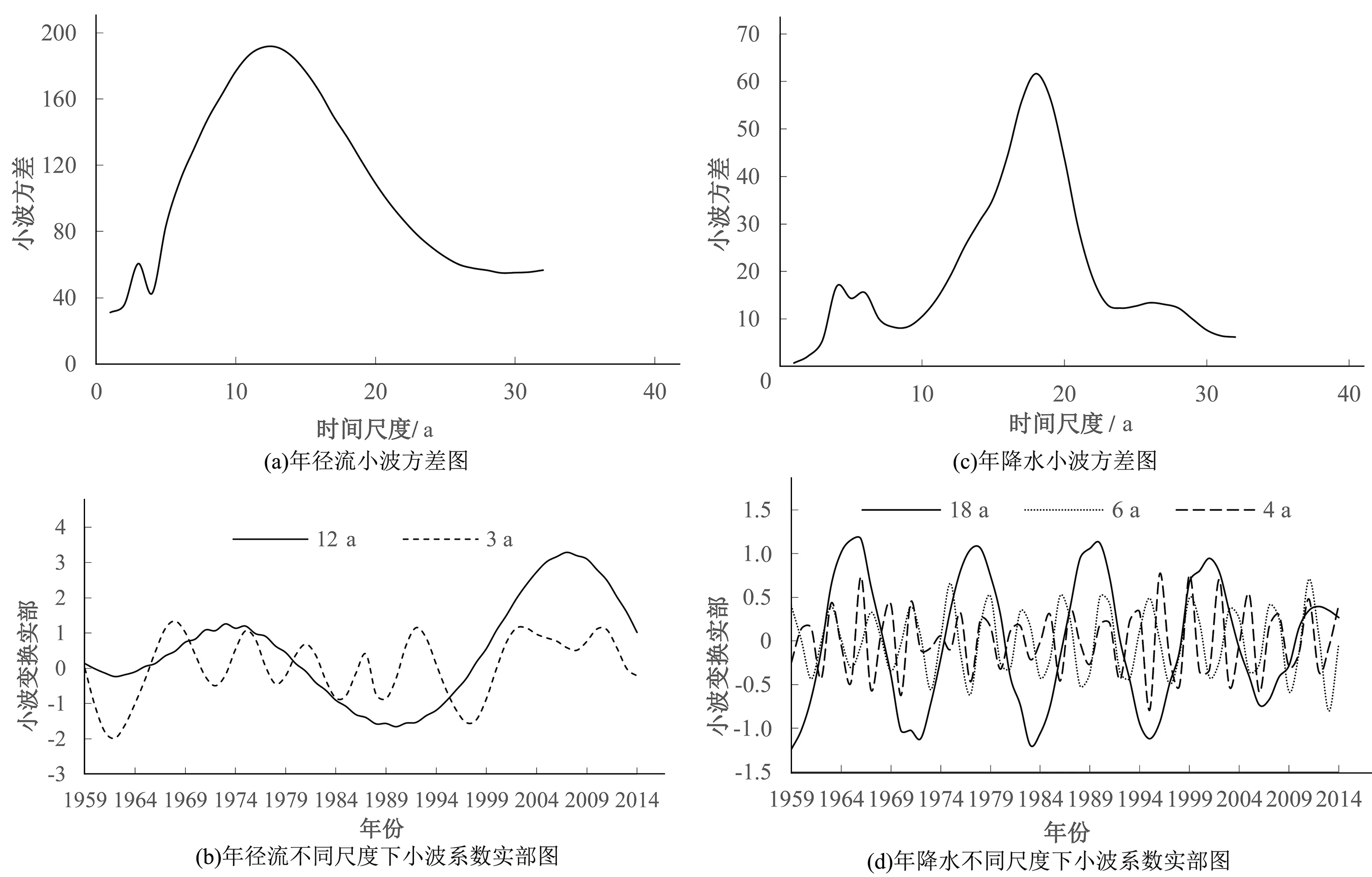
圖3 年徑流和年降水時間序列小波方差圖及不同尺度下小波實部圖Fig.3 Wavelet variance diagram and wavelet real parts under different scales of runoff and precipitation time series data

3.2 徑流與降水量相關關系分析

基于上述小波變換，對五郎河年徑流量與麗江站年降水量的小波系數進行相關性分析，通過對連續小波變換后的系數進行交叉小波變換和小波相干變換，分析兩時間序列相互間的交叉小波能量譜和小波相干譜，進而探討兩者在不同時間尺度下時頻域的相關程度。圖4展示了五郎河流域徑流和麗江站降水量的交叉小波功率譜和小波相干譜。圖中箭頭表示兩者之間的位相關系，箭頭向右和向左分別表示徑流與降水之間為同位相和反位相，說明兩者呈正(負)相關關系，箭頭向下和向上分別表示降水變化超前和落后徑流變化90°。圖中細弧線以內區域為有效譜值[20]。從圖4(a)中可以看出，總管田站徑流與麗江站降水存在：①1～4 a(1964-1970年)的周期，呈現較好的正相關，高能量區主要集中在低中頻部分的1～3 a，且從低頻向高頻區逐漸過渡；②1～3 a(1994-1999年)、2～3 a(2003-2006年)、5～7 a(1977-1981年)的共振周期，置信度檢驗的區域相對較小，表現出間歇性的準周期振蕩。

兩序列的小波凝聚譜顯示[圖4(b)]，徑流與降水具有非常好的正相關性，通過顯著性檢驗的區域占整個有效譜值區域范圍內的90%左右，在4～6 a的周期上，1970年和1990年前后，其共振周期發生了突變，說明五郎河流域在該時段發生了“豐-枯”周期的轉變。兩序列的共振周期高能量區主要分布在1968年前后和1985年前后2 a、1970-1995年6 a左右的周期，以及1975-2000年的12 a左右的周期。

結合交叉小波能量譜和交叉小波凝聚譜，發現：①五郎河流域徑流與麗江站降水變化存在2～4 a的顯著性共振周期，說明降水對徑流的影響很大。②兩者表現為非常顯著的正相關性，說明麗江站降水量可作為五郎河流域徑流預測的控制因素。③徑流和降水在1970和1990年前后發生了“豐-枯”的突變。

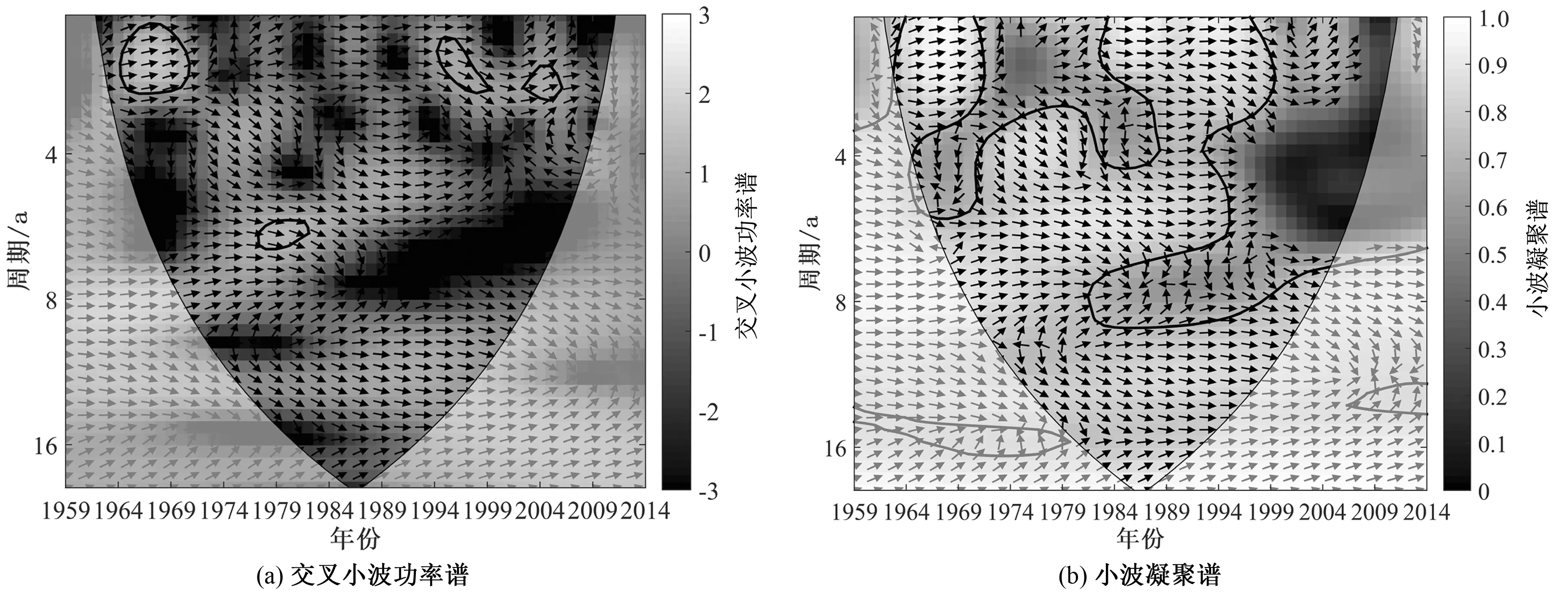
圖4 徑流與降水的交叉小波功率譜與小波凝聚譜Fig.4 Cross-wavelet power spectrum and squared wavelet coherence between the runoff and precipitation time series

4 結 論

本文通過對五郎河總管田水文站和麗江氣象站56年間的數據進行小波分析，得到五郎河徑流量和麗江站降水的周期特性，并運用交叉小波變換，分析了它們在時頻域中的相關關系，具體結論如下：

(1)通過小波變換的系數實部、模平方等值線圖及小波方差圖，可知，五郎河流域總管田水文站的徑流量在1959-2014年間豐枯變化明顯，存在6～28 a和2～5 a 2種尺度的周期變化，其中12 a是第一周期，3 a強度略弱，是第二周期。同時預測2014年后徑流均有減少的趨勢，且在12 a時間尺度下，2022年前后徑流將由枯變豐；

(2)通過對降水序列的統計特性分析和小波分析，可知，麗江站降水存在16～28 a、9～14 a和4～8 a 3種尺度的周期變化規律，其中18 a為第一周期，4 a、6 a分別為第二和第三周期；同時預測在18 a時間尺度，2024年左右降水量將由少變多；

(3)交叉小波凝聚譜和小波相干功率譜顯示，總管田站年均徑流與麗江站年降水存在2～4 a的顯著性的共振周期，且兩者呈現出非常好的一致性，說明麗江站降水量可作為五郎河流域徑流預測的控制因素。

(4)五郎河徑流量變化是各種水文氣象因子多重交互作用的結果，其中降水變化是徑流變化的主導因素之一，但徑流的變化與其他多重氣象因子之間的交互影響有待進一步研究。此外，在本文中采用的時間尺度為年，而無法體現年內的細節變化，還需更深入的分析和研究。

□

[1] 王文圣, 丁 晶, 李躍清, 等. 水文小波分析[M]. 北京: 化學工業出版社, 2005.

[2] 桑燕芳, 王中根, 劉昌明. 小波分析方法在水文學研究中的應用現狀及展望[J]. 地理科學進展, 2013,32(9):1 413-1 422.

[3] 張少文, 丁 晶, 廖 杰, 等. 基于小波的黃河上游天然年徑流變化特性分析[J]. 四川大學學報: 工程科學版, 2004,36(3):32-37.

[4] Grinsted A, Moore J C, Jevrejeva S. Application of the cross wavelet transform and wavelet coherence to geophysical time series[J]. Nonlinear Processes in Geophysics, 2004,11(5/6):561-566.

[5] 孫衛國, 程炳巖. 交叉小波變換在區域氣候分析中的應用[J]. 應用氣象學報, 2008,19(4):479-487.

[6] 余丹丹, 張 韌, 洪 梅, 等． 基于交叉小波與小波相干的西太平洋副高與東亞夏季風系統的關聯性分析[J]. 南京氣象學院學報, 2007,30(6):755-769.

[7] Torrence C, Compo G P. A practical guide to wavelet analysis[J]. Bulletin of the American Meteorological Society, 1998,79(1): 61-78.

[8] Lau K M, Weng H Y. Climate signal detection using wavelet transform: How to make a time series sing[J]. Bulletin of the American Meteorolgical Society, 1995,76(12):2391-2 402.

[9] 安 全, 梁 川, 劉 政. 雅礱江中上游徑流變化特性的小波分析[J]. 武漢大學學報(工學版), 2008,41(3):20-28.

[10] 馬海波，郭慧芳，董增川, 等. 鄱陽湖出湖徑流序列的多時間尺度小波分析[J]. 人民長江,2011,42(11): 53-55.

[11] 薛小杰, 蔣曉輝, 黃 強, 等. 小波分析在水文序列趨勢分析中的應用[J]. 應用科學, 2002,20(4):426-428.

[12] Torrence C, Webster P J. Interdecadal Changes in the ENSO-Monsoon system[J]. Journal of Climate, 1999,12:2 679-2690.

[13] 丁裕國, 江志紅.氣象數據時間序列信號處理[M].北京:氣象出版社, 1998:278-283.

[14] Maraun D，Kurths J. Cross wavelet analysis: significance testing and pitfalls[J]. Nonlinear Processes in Geophysics, 2004,11(4):505-514.

[15] Nakken M. Wavelet analysis of rainfall runoff variability isolating climatic from anthropogenic patterns[J]. Environmental Modelling & Software, 1999,14(4):283-295.

[16] Nason G P, Sapatinas T. Wavelet packet transfer function modelling of nonstationary time series[J]. Statistics and Computing, 2002,12(1):45-56.

[17] 鄧凱旭, 宋寶瑞. 小波變換在金融數據分析中的應用[J]. 數理統計與管理, 2006,25(2):215-219.

[18] Chen J X, Wang W J. Wavelet-based interpolation of medical images[J]. Journal of System Simulation, 2007,19(1):145-149.

[19] 劉笑彤, 蔡運龍. 基于小波分析的徑流特性和影響因素多尺度分析----以通天河為例[J]. 北京大學學報(自然科學版), 2014,50(3):549-556.

[20] 邵 駿. 基于交叉小波變換的水文多尺度相關分析[J]. 水力發電學報, 2013,32(2):22-26.