淺談拋物線幾何性質的幾何證明

■鄭州外國語學校 楊春波

數學篇

淺談拋物線幾何性質的幾何證明

■鄭州外國語學校 楊春波

拋物線的一些幾何性質想必大家是熟悉的:如圖1,拋物線y2=2px(p＞0)的焦點為F,準線為l。過點F作傾斜角為α(0＜α＜π)的直線與拋物線交于A、B兩點,設A(x1,y1), B(x2,y2),M為AB的中點,由A、M、B向準線l作垂線,垂足分別為D、N、C,連接圖中剩余各線段,則有:

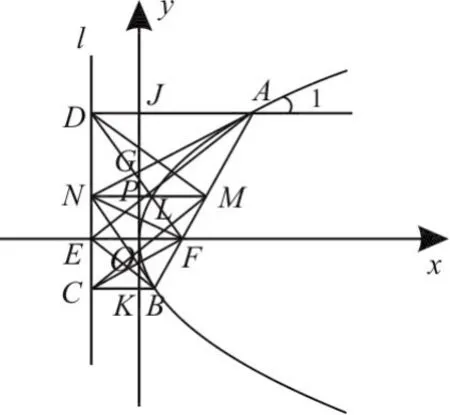
圖1

(4)以AB為直徑的圓與準線l相切。

(5)點A、O、C三點共線,點B、O、D三點共線。

證明拋物線的以上幾何性質時多用代數方法(即聯立直線與拋物線的方程),既然是幾何性質,為何不用幾何證法呢?而且,相對于橢圓和雙曲線來說,拋物線的定義自有優勢:平面內與一個定點和一條定直線(定直線不經過定點)距離相等的點的軌跡。現把拋物線幾何性質的幾何證明,展示如下。

證明:

因此,|AB|≥2p,當且僅當sin2α=1,即時,等號成立。這就是“通徑在過焦點的所有弦中弦長最短,其長度為2p”。(3)得證。

由AD∥BC及AF=AD,BF=BC,易證∠DFC=90°。在Rt△DFC中,FE為斜邊上的高,由射影定理知EF2=ED·EC,即y1y2=-p2。

Rt△DFC中,FN為斜邊上的中線,則FN=NC=ND,從而易證△ADN≌△AFN (或△BCN≌△BFN),得∠NFM=90°,即NF為Rt△ANB斜邊上的高,則NF2= AF·BF,從而:

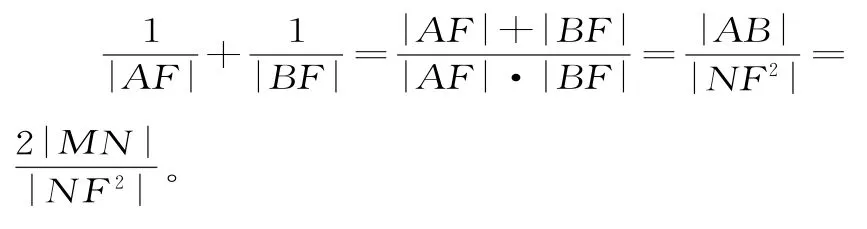
易知|AB|=x1+x2+p。

由|AF|=|AD|=|EF|+|AF|cosα= p+|AF|cosα,得

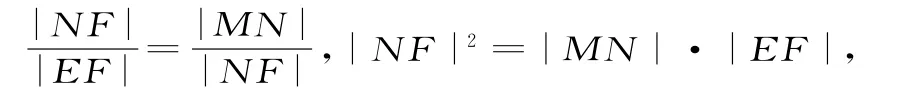
設G為AN與DF的交點,H為BN與CF的交點,則G、H分別為DF和CF的中點。在△DEF中,G為DF的中點,O為EF的中點,故OG為△DEF的中位線,OG∥DE,點G在y軸上。同理,點H也在y軸上。而且易知G、H分別是OJ和OK的中點。

兩式相乘,得AJ·BK·(OF)2= (OG·OH)2=(OF)4,AJ·BK=(OF)2,即至此(1)得證。

設AC與x軸的交點為O',則:

因此,|O'E|=|O'F|,O'為EF的中點,則O'與O重合,A、O、C三點共線。同理, B、O、D三點也共線,(5)得證。

值得一提的是,對于圖1,有同學挖掘出了另外一些相關的幾何性質和幾何證明,補充在這里與大家分享。

(6)設L為MN與拋物線的交點,則L為MN的中點。

證明:在Rt△NFM中,由拋物線的定義知|LF|=|LN|,從而易證FL為斜邊上的中線,則|LM|=|LN|,L為MN的中點。

(7)EF平分∠AEB。

證明:由知 Rt△ADE∽Rt△BCE,則∠AED=∠BEC,∠AEF=∠BEF,EF是∠AEB的平分線。(8)以AF或BF為直徑的圓與y軸相切。

證明:設M1為AF的中點,則:

故以AF為直徑的圓與y軸相切。同理,可證以BF為直徑的圓也與y軸相切。

(9)NA、NB均是拋物線的切線。

證明:如圖1,由∠FAN=∠DAN=∠1,結合拋物線的光學性質(從焦點出發的光線,經過拋物線上的一點反射后,反射光線平行于拋物線的軸),知NA是拋物線的切線。同理,NB也是拋物線的切線。

由此可見,拋物線的焦點弦在兩端點處的切線互相垂直,且兩切線的交點恰在拋物線的準線上,而且由NF⊥AB可知,兩切線的交點與拋物線焦點的連線與焦點弦垂直。

眾所周知,解析幾何的基本思想是用代數方法研究幾何問題,其最基本的研究方法為坐標法。但是,事物是一分為二的,如果過分強調坐標法,久而久之,人們就會習慣于將解析幾何與繁難的運算等價起來,這樣的認識是片面的。我們應該清楚地認識到,解析幾何的研究對象是幾何圖形,因此,在解答解析幾何問題時,要注重挖掘問題的幾何特征,不妨用幾何的眼光審視解析幾何問題。更多的例證留給同學們去探索、去發現。

練一練:

1.已知拋物線y2=2px(p＞0)的焦點弦AB的兩個端點分別為A(x1,y1),B(x2, y2),則的值一定等于( )。

A.-4 B.4 C.p2D.-p2

2.(2014·課標全國Ⅱ)設F為拋物線C:y2=3x的焦點,過F且傾斜角為30°的直線交C于A、B兩點,則|AB|等于( )。

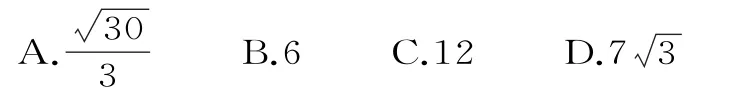
3.過拋物線y2=4x的焦點F的直線交拋物線于A、B兩點,點O是坐標原點,則|AF|·|BF|的最小值為( )

4.設拋物線x2=12y的焦點為F,經過點P(2,1)的直線l與拋物線交于A、B兩點,且P恰為AB的中點,則|AF|+|BF|=____。

參考答案:1.A2.C3.C4.8

(責任編輯 徐利杰)