例析圓錐曲線中的探索性問題
■重慶市鐵路中學 何成寶
例析圓錐曲線中的探索性問題
■重慶市鐵路中學 何成寶
圓錐曲線中的探索性問題,是同學們在學習圓錐曲線時經常遇到的一類問題,面對此類問題,同學們往往束手無策,難以順利解決。下面舉例說明,以供同學們參考。
一、橢圓
已知常數a>0,在矩形ABCD中,AB=4,BC=4a,O為AB的中點,點E、 F、G分別在BC、CD、DA上移動,且=P為GE與OF的交點(如圖1),問是否存在兩個定點,使P到這兩點的距離的和為定值。若存在,求出這兩點的坐標及此定值;若不存在,請說明理由。

圖1
解析:根據題設條件,首先求出點P的坐標滿足的方程,據此再判斷是否存在兩定點,使得點P到兩點距離的和為定值。
解得坐標分別為:A(-2,0),B(2,0), C(2,4a),D(-2,4a)。
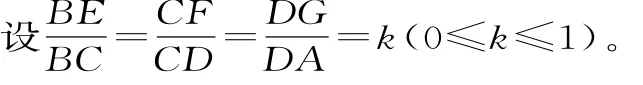
解得坐標分別為E(2,4ak),F(2-4k, 4a),G(-2,4a-4ak)。
直線OF的方程為:
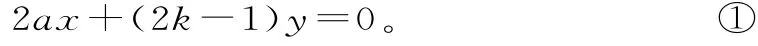
直線GE的方程為:

①②聯立消去參數k,得點P(x,y)的坐標滿足方程2a2x2+y2-2ay=0。
二、雙曲線
解析:假設存在直線m,它與雙曲線的交點Q1、Q2的坐標分別為Q1(x1,y1),Q2(x2, y2),則:

兩式相減,得:

則2(x1-x2)=y1-y2。
直線m的方程為y-1=2(x-1),即y=2x-1。
2x2-4x+3=0。
Δ=(-4)2-4×2×3=-8<0。
因此,直線y=2x-1與雙曲線不相交,題設中的直線是不存在的。
在研究直線與圓錐曲線有關的問題時,應注意對判別式的討論。
三、拋物線
在以O為原點的直角坐標系中,點A(4,-3)為△OAB的直角頂點,已知|AB|=2|OA|,且點B的縱坐標大于零。
(2)求圓x2-6x+y2+2y=0關于直線OB對稱的圓的方程。
(3)是否存在實數a,使拋物線y= ax2-1上總有關于直線OB對稱的兩個點?若不存在,說明理由;若存在,求出a的取值范圍。
解析:(1)設,則由得
由條件可知圓的標準方程為(x-3)2+ (y+1)2=10,圓心為(3,-1),半徑為。
設圓心(3,-1)關于直線OB的對稱點為(x0,y0),則:得故所求圓的方程為(x-1)2+(y-3)2=10。
(3)設P(x1,y1),Q(x2,y2)為拋物線上關于直線OB對稱兩點,則:
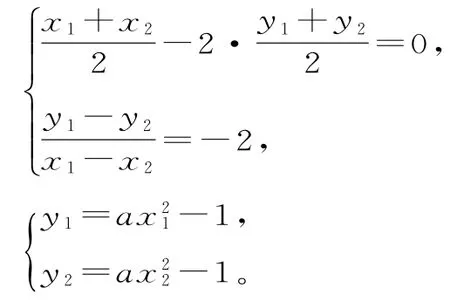
x1,x2為方程的兩個相異實根,于是由解得
以上三個例題,分別是橢圓、雙曲線、拋物線與直線的關系中的探索性問題。探索性問題,由于沒有明確的結論,方向不明,自由度大,要去探索研究。因此,學好圓錐曲線中的探索性問題,能夠很好地培養同學們的創新意識和應用能力。
(責任編輯 徐利杰)
啟事:隨著高考制度的不斷改革,全國參加高校自主招生的學生越來越多,為了更好地備戰自主招生考試,本刊編輯部決定于今年5月份出版一期增刊,主要內容為全國部分高校自主招生面試、筆試典型題歸類解析,定價6元,郵寄費1元。歡迎訂閱。郵局匯款: (450004)鄭州市順河路11號《中學生數理化》(高中)編輯部。收款人:王福華。轉賬匯款:中國郵政儲蓄,戶名王福華,卡號6221884910016853274。
本刊編輯部

