初中一次函數現實背景模型探究

摘要:數學根植于生活并應用于生活,數學模型來自于現實世界,模型思想的建立是學生體會和理解數學與外部世界聯系的基本途徑;探究一次函數現實背景模型,有利于學生理解一次函數中兩個變量間的對應關系及其圖象和性質,并利用一次函數的圖象和性質解決實際問題.
關鍵詞:一次函數;現實背景;模型探究
作者簡介:周占鋒(1963-),男,福建省龍巖市武平縣,本科,高級教師,武平縣教師進修學校中學教研室主任.數學建模是數學學科六個核心素養之一,而模型思想是初中數學的重要數學思想.數學課程標準(2011年版)指出:數學與人類發展和社會進步息息相關,隨著現代信息技術的飛速發展,數學更加廣泛應用于社會生產和日常生活的各個方面. 課標把模型思想作為十個核心概念之一,認為模型思想的建立是學生體會和理解數學與外部世界聯系的基本途徑.一次函數是初中學生學習和理解函數的重要素材,其中自變量與函數的對應關系是初學者理解兩個變量間對應關系的難點,探究一次函數現實背景模型,有利于學生理解一次函數中兩個變量間的對應關系及其圖象和性質,并利用一次函數的圖象和性質解決實際問題.以下是幾種一次函數的現實背景模型探究.
一、行程問題的一次函數現實背景模型
設路程為s,速度為v,時間為t,則s=vt . 當速度v為常量,如v=30km/s,s=30t是正比例函數;而正比例函數是最特殊的一次函數. 若行程問題中出現兩個或兩個以上對象,不同時間段有不同的位置狀態,就構成一次函數的分段函數模型.
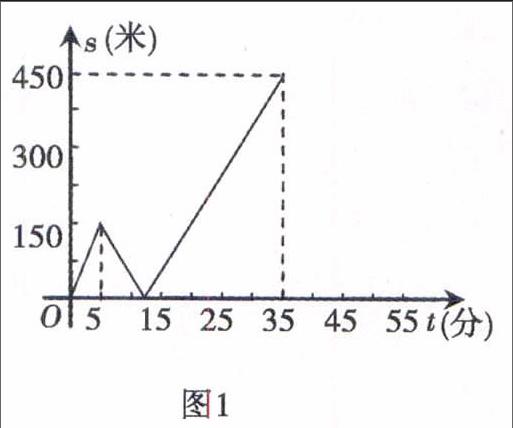
例1甲乙兩人勻速從同一地點到1500米處的體檢中心體檢,甲出發5分鐘后,乙以50米/分的速度沿同一路線行走,s關于t的函數圖象的一部分如圖1所示.設甲乙兩人相距s(米),甲行走的時間為t(分).
(1)求甲行走的速度;
(2)在坐標系中,補畫s關于t函數圖象的其余部分;
(3)問甲、乙兩人何時相距360米?
分析此現實背景中出現甲、乙兩人為兩個不同對象,出發時間不同使各個時間段兩人的相對位置不同,構成距離s與時間t在不同時間段有各自不同的一次函數對應關系,其中題設信息以文字信息和圖象信息相結合的形式出現,從圖象信息發現背景涉及四種不同情形:
①t=5分鐘時甲走了150米;
②甲出發5分鐘后,乙開始出發,t=12.5分鐘時,甲追上乙,s=0;
③t=35分鐘時,甲走了1050米;乙用時30分鐘走了1500米,到達體檢中心,s=450米;
④t>35分鐘時,乙已到達體檢中心,甲還要用15分鐘走完450米的路程,t=50分鐘時甲也到達體檢中心,s=0.
根據以上分析s與t的函數關系式是:
s=30t(0≤t≤5)
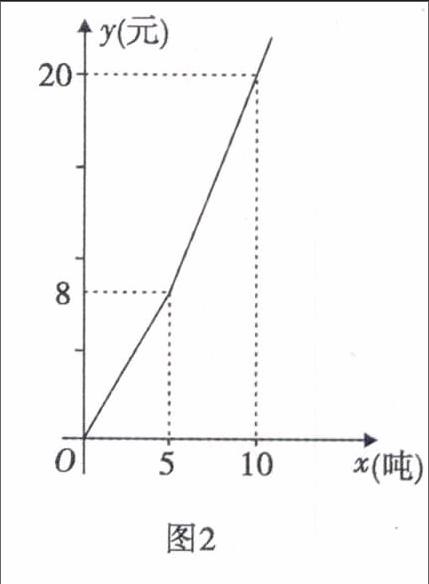
-20t+250(5 20t-250(125 -30t+1500(35 試題設計要點: 1.基礎題設置:從圖象信息中發現甲5分鐘走的路程為150米,可求甲行走的速度為30米/分. 2.對實際問題的再現:t=35分鐘時,乙實際用時30分鐘,乙已經到達圖書館,此時s=450米,甲用時t=15分鐘才能到達圖書館,此時s=0. 在坐標系中,補畫s關于t函數圖象的其余部分是連接(35,450),(50,0)的一條線段. 3.設甲、乙兩人t分鐘后相距360米,此處的難點是乙實際用時為(t-5)分鐘,而不是t分鐘,根據圖象信息時間應在12.5 二、收費問題的一次函數現實背景模型 收費問題通常與兩種或兩種以上的收費方式相關,收費金額有的與時間建立一次函數關系,有的與用量建立一次函數關系. 例2(2014龍巖中考第23題)隨著地球上的水資源日益枯竭,各級政府越來越重視倡導節約用水.某市對居民生活用水按“階梯水價”方式進行收費,人均月生活用水收費標準如圖2所示.圖中x表示人均月生活用水的噸數,y表示收取的人均月生活用水費(元).請根據圖象信息,回答下列問題: (1)該市人均月生活用水的收費標準是:不超過5噸,每噸按元收取;超過5噸的部分,每噸按元收取; (2)請寫出y與x的函數關系式; (3)若某個家庭有5人,五月份的生活用水費共76元,則該家庭這個月用了多少噸生活用水? 水費問題通常采用“階梯水價”方式進行收費,水費與用水量建立一次函數的分段函數現實背景模型,考查學生從現實生活中抽象出一次函數模型的數學思考,并用數學思考進行問題解決的考量. 三、銷售問題的一次函數現實背景模型 銷售問題通常以何種銷售、銷售單價與銷售量為現實背景模型出現,多數是利潤與銷售量建立一次函數關系的模型,關注利潤的合理區間. 有時通過圖象信息提供已知條件,考查學生的讀圖能力. 例3(2016龍巖中考第23題)某廠家在甲、乙兩家商場銷售同一商品所獲利潤分別為y甲、y乙(單位:元),y甲、y乙與銷售數量x(單位:件)的函數關系如圖3所示,試根據圖象解決下列問題: (1)分別求出y甲、y乙關于x的函數關系式; (2)現廠家分配該商品800件給甲商場,400件給乙商場,當甲、乙商場售完這批商品后,廠家可獲得總利潤是多少元? 該題以圖象信息顯示問題背景,突現從實際生活中抽象出一次函數模型解決實際問題的能力,考查用解析法求解一次函數解析式. 四、圖形運動的一次函數現實背景模型 圖形運動通常有點動、線動和面動等,其構成的軌跡、距離、面積等可以用函數來刻畫,初中數學常有用一次函數刻畫圖形運動的情況. 例4已知如圖4,在矩形ABCD中,動點P從點B出發,沿BC,CD,DA運動至點A停止.設點P運動的路程為x,△ABP的面積為y,如果y關于x的函數圖象如圖5所示,則△ABC的面積是() A.10B.16C.18D.20 分析此模型是由點動而產生面動,觀察圖4,動點P從點B出發,到點C位置時△ABC的面積最大;動點P從點C運動到點D,△ABC的面積保持最大數值不變;從點D運動到點A,△ABC的面積由最大值變為0.這一變化過程在圖5的函數圖象中得到充分刻畫.由圖5可知:BC=4,DC=AB=5,S△ABC=12×4×5=10答案是A. 現實背景模型的探究和建立飽含了教師的智識,教師只有不斷加強業務學習,細心觀察和品味現實生活中的事物關聯性才能使教學有的放矢,課標對建立和求解模型的觀察作了很好的闡述:從現實生活或具體情境中抽象出數學問題,用數學符號建立方程、不等式、函數等表示數學問題中的數量關系和變化規律,求出結果并討論結果的意義.函數教學中重視現實背景模型的探究,有利于學生理解函數的概念,掌握從現實背景中抽象出函數模型的方法,學會用函數思想刻畫事物的變化規律,提高課堂教學的有效性.

