無中生圓,圓滿解題
韓菲菲


[摘 要] 對于表面上純屬直線型問題的幾何問題題型,拋開原始的解題思路,提取相關條件,巧添輔助圓,利用圓冪定理解題,可化繁為簡,化難為易. 本文由一道競賽題展開聯想,通過幾個例題來分析如何巧添輔助圓并解題.
[關鍵詞] 輔助圓;圓冪定理;幾何問題
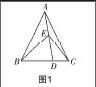
[1992年全國聯賽] 如圖1,在△ABC中,AB=AC,D是底邊上一點,E是線段AD上一點,且∠BED=2∠CED=∠BAC,求證:BD=2CD.
所以∠ECF=90°.
易證△EFG≌△EFC(AAS),
所以∠FEG=∠CED,GF=CF.
因為∠BEF=2∠CED,
所以∠BEG=∠GEF.
可證△BEG≌△FEG(ASA),
所以BG=GF=CF.
所以BF=2CF.
根據角平分線性質得BD=2CD.
有比較,才知優越. 我們發現方法二更完美,究其原因,在于圓. 圓是最美妙的幾何圖形. 圓的根基是弧,且具有完美對稱性,具有很多圓冪定理,所以能用好圓,領悟圓,會讓我們解題舉重若輕,充滿創造性. 在處理平面幾何中的許多問題時,需要借助圓的性質使問題得以更好地解決,但是我們所需要的圓卻并不存在,這就需要我們利用已知條件,做到“無中生圓”.
下面結合幾個例題簡單地談一下如何根據具體情境生圓,做到圓滿解決.
利用圓的定義生圓
解析 因為AB=AC=AD,所以以點A為圓心,AB為半徑作圓,點B,C,D均在圓上. 利用△ABC為等腰三角形,且AE為中線得到AE為高,又因為AE=EC,由圓周角定理等條件計算得到∠EAC=45°,∠BAC=90°,∠BDC=45°,∠DBC=30°.
此時只需對△DBC進行分析即可,得到BC=12,所以AB=12.
利用直徑所對的圓周角是直角
的條件生圓
例2 如圖5,已知Rt△ABC中,AC=5,BC=12,∠ACB=90°,P是邊AB上的動點,Q是邊BC上的動點,且∠CPQ=90°,求線段CQ的取值范圍.
利用四邊形對角互補生圓
例3 如圖7,在矩形ABCD中,AB=6,以點B為直角頂點作等腰直角三角形BEF,連接AE,AF,當AE⊥AF且AE︰AF=1︰2時,AE的長是多少?
解析 由∠EAF+∠EBF=180° 可得點A,E,B,F四點共圓,再結合托勒密定理可以得到AB·EF=AE·BF+BE·AF.
設AE=x,代入得到方程
同底同側張等角生圓
例4 如圖8,在△ABC中,CE⊥AB,BD⊥AC,∠A=60°,求證:BC=2DE.
類似以上這樣的,表面上純屬直線型問題,但利用直線型的有關知識解答會很繁雜,甚至有的很難找到解決問題的思路和途徑. 但如果對題設進行認真分析,仔細觀察圖形,便可挖掘題設中所蘊含的內在條件,提取相關條件,巧添輔助圓,溝通與圓的內在聯系,調取圓內的相關圓冪定理和性質,為解題提供了新的途徑,把圓的有關性質在解題中進行運用,可化繁為簡,化難為易.

