基于數值分析的樁-筏復合地基中的筏板應力分析
■曾俊鋮
(福建省高速公路有限責任公司,福州350001)
基于數值分析的樁-筏復合地基中的筏板應力分析
■曾俊鋮
(福建省高速公路有限責任公司,福州350001)
采用有限差分法分析程序,依據某試驗段的工程地質和設計施工情況建立了路堤荷載下樁-筏復合地基數值分析模型,計算分析了樁-筏復合地基中筏板結構上、下表面的三向應力分布規律及不同筏板厚度下的應力變化規律。結果表明筏板上表面橫向受壓、豎向受壓,下表面橫向受拉、豎向受壓,筏板的設計關鍵在于控制筏板下表面的橫向拉應力;筏板越厚,下表面的橫向拉應力分布越均勻,最大拉應力越小。研究成果可為路堤荷載作用下樁-筏復合地基中的筏板設計提供參考。
數值分析復合地基樁-筏應力
樁-筏復合地基是一個由鋼筋混凝土板、褥墊層、剛性樁及地基土等幾部分組成的(如圖1),具有有效地減小地基的不均勻沉降和工后沉降,提高地基的承載力、路基穩定性,縮短施工工期等優勢[1],在路基工程中的深厚軟土地基處理中得到應用[2-3]。
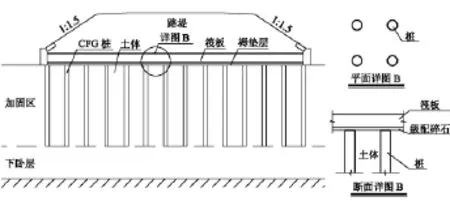
圖1 樁-筏復合地基加固示意圖
樁-筏復合地基控制沉降的性能優于帶帽樁-網復合地基,但造價要比帶帽樁-網復合地基高,主要是筏板的造價比樁帽的高。因此,有必要對路堤荷載下樁-筏復合地基中的筏板結構三向應力分布情況進行研究。本文采用有限差分法分析程序,建立了路堤荷載下樁-筏復合地基數值分析模型,計算分析了樁-筏復合地基中筏板結構上、下表面的三向應力分布規律及不同筏板厚度下的應力變化規律,為筏板的優化設計提供參考,以降低筏板造價。
1 樁-筏復合地基數值模型
1.1 模型參數確定
該模型的的工程地質參數和設計施工情況見文獻[1];同時,軟硬塑黏土、硬塑黏土、全風化巖、強風化巖的承載力特征值分別為150kPa、200kPa、250kPa、500kPa。數值模型的土層的彈性模量按壓縮模量3.5倍取值,全風化巖、強風化巖的彈性模量根據土層承載力特征值由硬塑黏土的模量進行正比例換算,路基的各物理力學參數指標取值見表1。
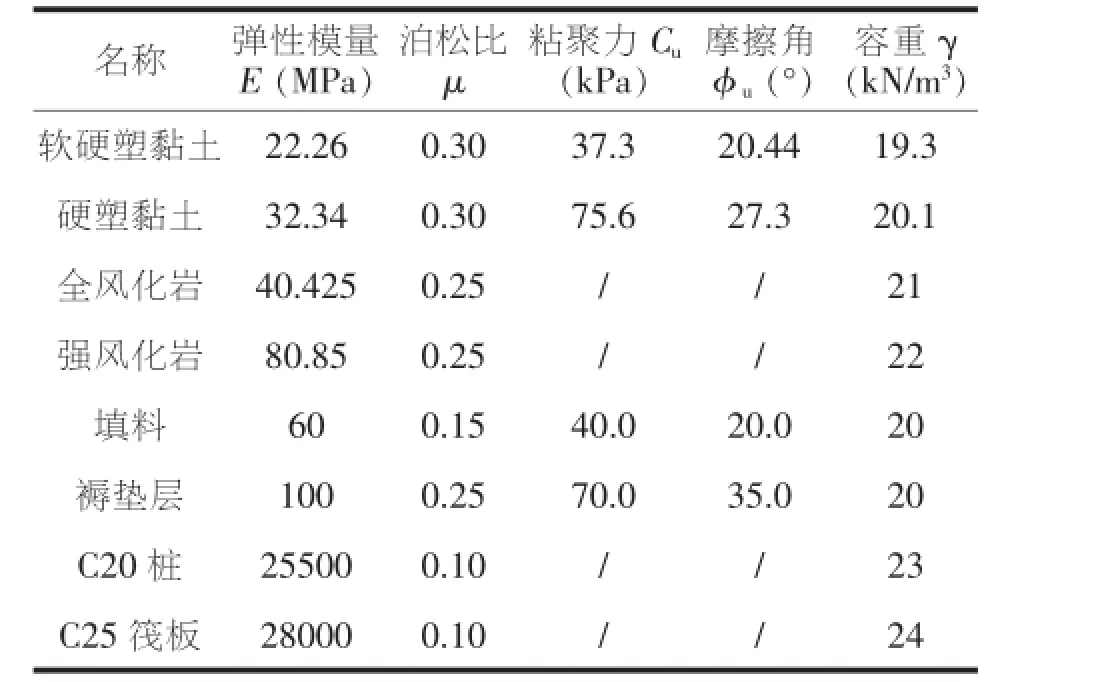
表1 路基的物理力學指標取值
地基軟硬塑黏土厚6.0m、硬塑黏土厚6.0m、全風化巖厚3.0m、強風化巖厚5.0m;剛性樁樁長13.0m,樁間距2.0m,樁直徑0.4m,采用正方形布置,混凝土強度等級C20;褥墊層結構為0.2m級配碎石;筏板為鋼筋混凝土板,厚度0.5m,混凝土強度等級C25。路基頂面寬13.6m,邊坡坡度1∶1.5,路堤填筑高度取4.8m。
1.2 數值模型建立
地基土、樁、筏板、褥墊層及路堤采用實體單元模擬。筏板與填料及褥墊層界面、樁與土界面處分別設置接觸單元。筏板和樁體采用彈性本構模型,其余路堤填料及地基土采用Mohr理想彈塑性本構模型。邊界條件是模型底部為完全固定約束,模型側面水平固定約束。因路基橫斷面沿路基中心線是對稱的,數值模型按半斷面建立。地基土的計算寬度為半路堤底部寬度的3倍;深度為達到弱風化層頂面,即假定弱風化層不發生沉降;縱斷面選取1倍的樁間距作為計算范圍。建立路堤荷載下樁-筏復合地基數值模型,如圖2所示。
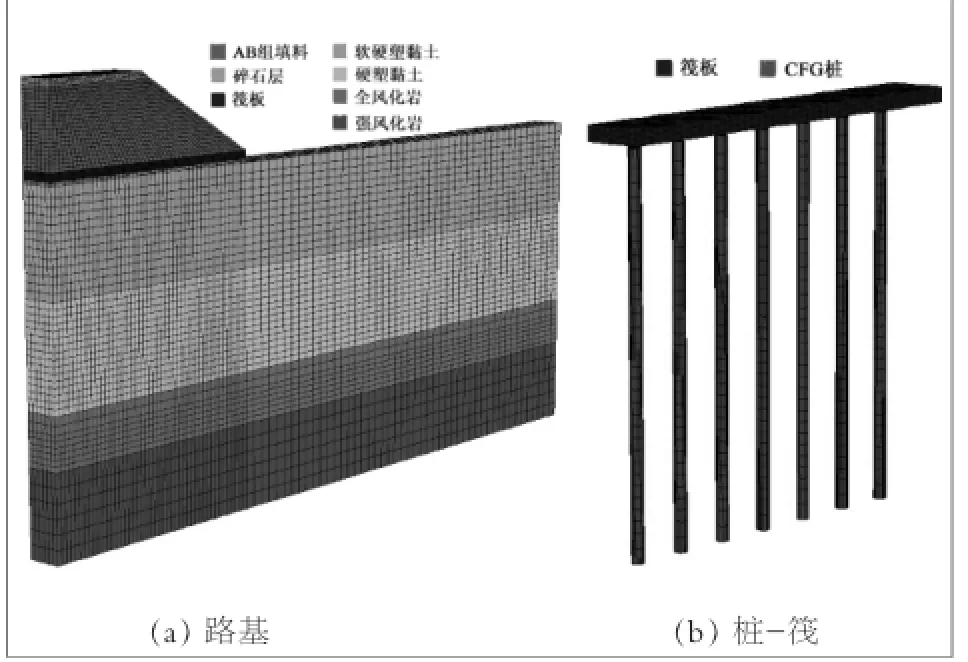
圖2 路堤荷載下樁-筏復合地基的路基數值模型
2 筏板上表面應力分布
為了能夠直觀的表示出應力分布的規律和幅值,本文將筏板的三向應力分布結果繪制成三維圖。圖中的正值表示拉應力,負值表示壓應力;SXX、SYY、SZZ分別代表σx(橫向)、σy(縱向)、σz(豎向)。
2.1 σx分布
圖3為筏板上表面σx(Pa)分布三維圖。從圖3可知:樁-筏復合地基在4.8m高的路堤荷載作用下,筏板上表面的σx為壓應力,最大壓應力位于X=6m和X=8m處,最大壓應力約為700kPa;越靠近樁位正上方,筏板上表面的σx越小。這是因為樁對筏板有向上的支承力,支承力會限制筏板局部(樁位正上方)變形,使得樁位正上方的筏板上表面出現受拉狀態,而下表面出現受壓狀態。通過結構力學的疊加原理,路堤荷載的作用和樁的作用疊加,就會出現如圖3所示的應力分布情況。
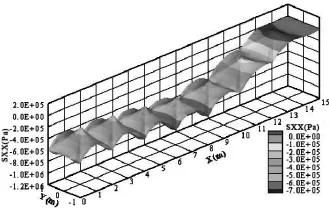
圖3 筏板上表面σx(SXX)分布三維圖
2.2 σy分布
圖4為筏板上表面σy(Pa)分布三維圖。從圖4可知:筏板上表面的σy有壓應力,也有拉應力,應力關于Y軸對稱。應力沿Y=0到Y=0.45m(或Y=-0.45m)的發展規律為:從拉應力狀態漸變為壓應力狀態,且拉、壓應力的數值大致相當,約為150kPa。
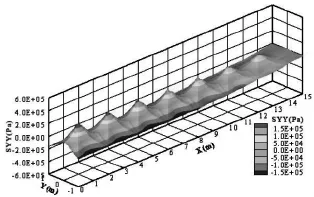
圖4 筏板上表面σy(SYY)分布三維圖
2.3 σz分布
圖5為筏板上表面σz(Pa)分布三維圖。從圖5可知:筏板上表面σz為壓應力,壓應力沿Y軸分布比較均勻。上表面σz沿X軸正向逐漸變小,與路堤橫截面形狀有關。在X=0~7m范圍,σz幅值在90~100kPa范圍內,與由σz=γH=20×4.8=96kPa相吻合。
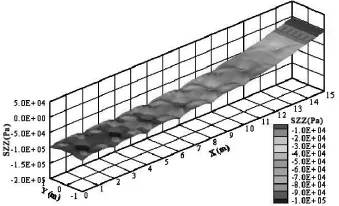
圖5 筏板上表面σz(SZZ)分布三維圖
3 筏板下表面應力分布
3.1 σx分布
圖6為筏板下表面σx(Pa)分布三維圖。從圖6可知:筏板下表面的σx為拉應力,最大拉應力約為1.0MPa,位于X=6.0m和X=8.0m處,混凝土未開裂。筏板下表面σx關于Y軸對稱,沿X軸正方向越來越小,越靠近樁位正上方,σx越小。
3.2 σy分布
圖7為筏板下表面σy(Pa)分布三維圖。從圖7可知:筏板下表面的σy有壓應力,也有拉應力,應力關于Y軸對稱,分布規律與筏板上表面的關于σy=0對稱。應力沿Y=0到Y=0.45m(或Y=-0.45m)的發展規律為:從壓應力狀態漸變為拉應力狀態,且拉、壓應力的數值大致相當,約為150kPa。

圖6 筏板下表面σx(SXX)分布三維圖
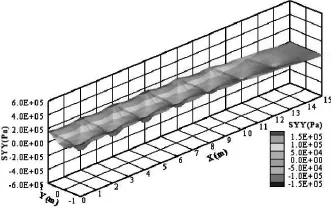
圖7 筏板下表面σy(SYY)分布三維圖
3.3 σz分布
圖8為筏板下表面σz(Pa)分布三維圖。從圖8可知:筏板下表面σz為壓應力,σz在樁頂上方出現明顯的應力集中現象。最大壓應力約為700kPa。
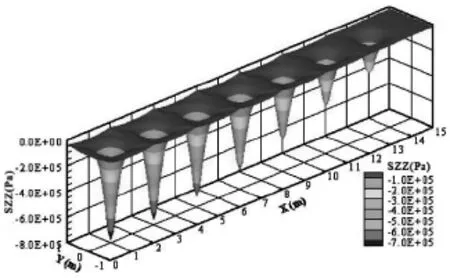
圖8 筏板下表面σz(SZZ)分布三維圖
4 筏板優化分析
筏板造價的影響因素主要是筏板的厚度和配筋率。一般情況下,路堤荷載作用下筏板的配筋按最小配筋率來設計,即筏板的配筋率取0.2%。在配筋率確定的情況下,筏板厚度成為控制筏板造價的最主要參數。通過筏板厚度的調整,分析不同筏板厚度下表面的σx分布,以優化筏板厚度。筏板厚度分別取0.2m、0.3m、0.4m、0.5m,分析結果如圖9所示。
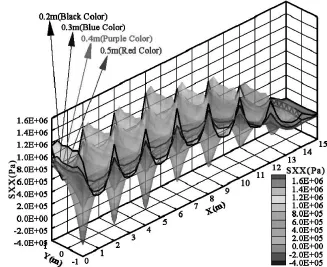
圖9 筏板不同厚度(0.2~0.5m)下表面σx(SXX)分布對比三維圖
從圖中可看出:在兩樁中心線位置,筏板厚度越厚,筏板下表面X向最大拉應力越小;在樁頂位置,筏板下表面σx的方向與筏板的厚度有關,筏板厚度較小時σx可能為壓應力;筏板越厚,筏板下表面的σx分布越均勻。說明筏板下表面的σx分布與筏板的厚度有關,即與筏板的剛度有關。筏板剛度越大,下表面的σx分布越均勻,X向最大拉應力越小。
5 結論
(1)筏板上表面的σx為壓應力;σy存在拉、壓應力,拉應力數值較小;σz為壓應力;下表面的σx為拉應力;σy存在拉、壓應力,拉應力數值較小;σz為壓應力。樁-筏復合地基在路堤荷載作用下,筏板的設計關鍵在于控制筏板下表面的σx(拉應力)的數值。
(2)筏板下表面的σx分布與筏板的厚度有關,即與筏板剛度有關。筏板剛度越大,下表面的σx分布越均勻,最大拉應力越小。
[1]張繼文,曾俊鋮,涂永明,等.京滬高速鐵路CFG樁-筏復合地基現場試驗研究[J].鐵道學報,2011,33(1):83-88.
[2]蔣宗全,趙同生,朱明,等.新建鐵路CFG樁樁筏復合地基試驗研究[J].鐵道建筑,2010(9):89-93.
[3]陳宏偉,徐林榮.樁-筏(網)復合地基樁土應力比現場測試研究[J].水文地質工程地質,2014,41(6):63-69.

