透視新定義類導數題

安徽 李昭平 (特級教師)

(作者單位：安徽省太湖中學)

透視新定義類導數題

在高等數學與高中數學的知識交匯處命題是近幾年高考命題的新趨勢, 其中以導數為載體的新定義類函數題屬高頻考點. 此類問題往往具有背景新、結構新、覆蓋面廣、綜合性強的特點，常常置于選擇題、填空題或解答題靠后的位置，成為高考試卷的亮點.下面結合典型試題透視五大考點，供大家復習時參考.

1.定義函數的凸性

【例1】先閱讀以下兩個定義.

定義1：若函數f(x)在區間D上可導，即f′(x)存在，且導函數f′(x)在區間D上也可導，則稱函數f(x)在區間D上存在二階導數，記作f″(x)，即f″(x)=[f′(x)]′.

定義2：若函數f(x)在區間D上的二階導數恒為正, 即f″(x)>0恒成立, 則稱函數f(x)在區間D上為下凸函數.

已知函數f(x)=x3+ax2+b在x=1處取得極值.

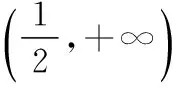
【解析】(1)因為f(x)=x3+ax2+b, 所以f′(x)=3x2+2ax.

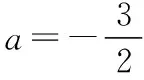
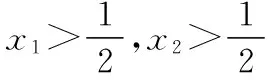
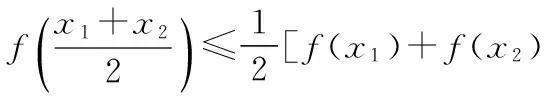
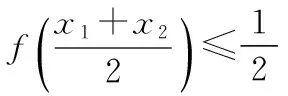
2.定義函數的駐點

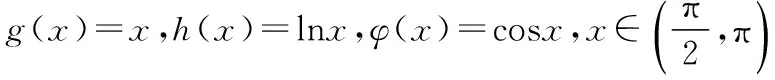
【解析】由g(x)=g′(x)，得x1=1.

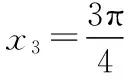
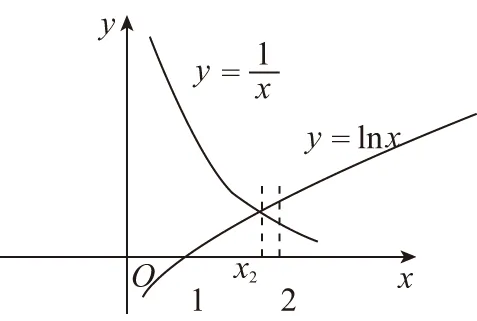
【評析】本題定義函數的“駐點”,主要考查學生閱讀、理解、遷移新知識的能力和數形結合的能力. 解題的基本步驟是：弄懂新定義，按定義求駐點，確定大小關系.

3.定義函數的拐點

( )

A.在直線y=-3x上

B.在直線y=3x上

C.在直線y=-4x上

D.在直線y=4x上

【解析】f′(x)=3+4cosx+sinx，f″(x)=-4sinx+cosx=0.由拐點的定義可知，f″(x0)=0，即4sinx0-cosx0=0，所以f(x0)=3x0+4sinx0-cosx0=3x0.

故M(x0，f(x0))在直線y=3x上. 選答案B.

【評析】本題以高等數學中函數的拐點與其二階導數的關系為背景，通過給出二階導數與函數拐點的定義(設置新情境)，考查學生閱讀、理解、遷移新知識的能力.結合函數的凸性可知，其實“拐點”的幾何意義是“函數圖象上凸、下凸的分界點”. 解題的基本步驟是：弄懂新定義，按定義列式，發現函數關系.

元朔二年（前127年），衛青率數萬騎兵從云中（今內蒙古托克托縣）出塞，沿黃河西進，到達高闕（，陰山西北的缺口），切斷了駐守黃河南原的樓煩王、白羊王與匈奴其他部落之間的聯系。

4.定義函數曲線的新切線

【例4】若直線l與曲線C滿足下列兩個條件：(1)直線l在點P(x0,y0)處與曲線C相切；(2)曲線C在P附近位于直線l的兩側，則稱直線l在點P處“切過”曲線C.

下列命題中正確的是________(寫出所有正確命題的編號).

①直線l:y=0在點P(0,0)處“切過”曲線C：y=x3;

②直線l:x=-1在點P(-1,0)處“切過”曲線C：y=(x+1)2;

③直線l:y=x在點P(0,0)處“切過”曲線C：y=sinx;

④直線l:y=x在點P(0,0)處“切過”曲線C：y=tanx;

⑤直線l:y=x-1在點P(1,0) 處“切過”曲線C：y=lnx.

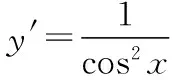
綜上，正確答案是①③④.

【評析】本題以高等數學中曲線的切線與曲線的位置關系為背景，在課本函數曲線的切線定義的基礎上再強化條件，得到直線l“切過”曲線C的新定義，主要考查導數的幾何意義和相關應用，以及數形結合的思想.

5.定義與導數有關的新函數

【例5】M是由滿足下列三個條件的函數f(x)構成的集合: ①方程f(x)-x=0有實根; ②函數f(x)的導函數f′(x)滿足0

求證：方程f(x)-x=0至多一個實數根.

【解析】由條件①，可以假設方程f(x)-x=0有兩個不相等的實數根α,β,則f(α)=α,f(β)=β,α<β.

由條件③知, 存在x0∈[α,β],使得等式f(β)-f(α)=(β-α)f′(x0)成立,即(β-α)(1-f′(x0))=0.

由條件②知，0

故方程f(x)-x=0至多有一個實數根.

(作者單位：安徽省太湖中學)