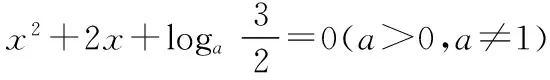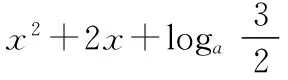集合問題常見的處理策略
山東 楊成武
(作者單位:山東省濱州市鄒平縣黃山中學(xué))
集合問題常見的處理策略

集合是高中數(shù)學(xué)一個最基本的概念,是表述數(shù)學(xué)問題的重要工具和載體.集合知識的基礎(chǔ)性地位,使其成為高考必考內(nèi)容.近年來,隨著高考能力立意思想的加強,對集合知識考查的深度、廣度和交匯度都在不斷增大.下面結(jié)合典型例題,介紹集合問題的處理策略.
一、用數(shù)軸解決集合間的包含關(guān)系
【解析】化簡得B={x|(x+3)(5-x)≥0}={x|-3≤x≤5}.由BA,得且等號不能同時取到,解得-8≤a≤2.經(jīng)檢驗,a=2和a=-8均滿足題意,所以實數(shù)a的取值范圍是{a|-8≤a≤2}.
【評注】P?Q的含義是:若x∈P則x∈Q;PQ的含義是:若x∈P則x∈Q,并且P≠Q(mào).在數(shù)軸上表現(xiàn)為一個區(qū)間完全落在另一個區(qū)間的內(nèi)部,但要注意端點是否包含.因此做此類題目一定要有檢驗環(huán)節(jié),比如中等號不能同時取到,可以求解之后再檢驗一下,否則容易得出錯誤答案.
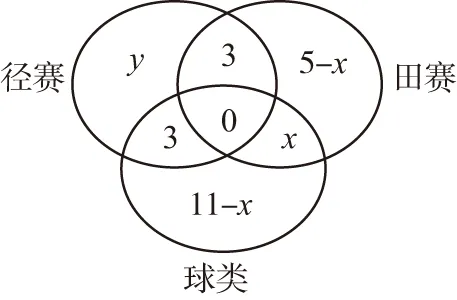
【變式1】已知集合A={x|-1 【解析】-a+1≤-1且3≤2a-1且-a+1<2a-1,且這兩個不等式中的“等號”不能同時取到,解得a>2. 【例2】已知集合A={x|-1 【解析】(法一)由于集合B的長度長于集合A的長度,又A∩B≠?,則集合A的兩個端點至少有一個在集合B所在的區(qū)間中,如圖(1),則a+3>-1;或如圖(2),則a<1. (法二)設(shè)A∩B=?,則a+3≤-1或a≥1,解得a≤-4或a≥1.由題意結(jié)合補集思想得出實數(shù)a的取值范圍是{a|-4 【評注】兩個數(shù)集之間有公共元素,也就是它們表示的區(qū)間有公共的點,通常我們可以利用數(shù)軸,比較兩個區(qū)間的端點即可,注意檢驗等號能否成立.本題采用補集思想解答顯然更簡潔. 【變式2】已知集合A=(-∞,-1]∪[2,+∞),B=[a,3-a],A∩B≠?,則實數(shù)a的取值范圍是________. (法一)比較區(qū)間端點可知A∩B≠?時,a≤-1或3-a≥2,解得a的取值范圍是a≤1. 【例3】在開秋季運動會時,某班級共有28名同學(xué)參加比賽,有15人參加徑賽,有8人參加田賽,有14人參加球類比賽,同時參加田賽和徑賽的有3人,同時參加徑賽和球類比賽的有3人,沒有同時參加三項比賽的同學(xué),問同時參加田賽和球類比賽的有多少人,只參加徑賽的同學(xué)有多少人? 【解析】畫出韋恩圖如圖所示,只參加徑賽的人數(shù)為y=15-3-3=9.設(shè)同時參加田賽和球類比賽的有x人,列式得9+3+5-x+3+x+11-x=28,化簡得31-x=28,解得x=3,故同時參加田賽和球類比賽的有3人,只參加徑賽的同學(xué)有9人. 【評注】對于涉及的集合信息較多或?qū)τ谖唇o元素的抽象集合,研究其關(guān)系或運算時,常可考慮用韋恩圖求解.畫出韋恩圖,將每一個區(qū)域內(nèi)的元素個數(shù)標出來. 【變式3】已知I為全集,集合M,NI,若M∩N=N,則 ( ) 【解析】因為M∩N=N,所以N?M,畫出韋恩圖(圖略),所以IM?IN. 【例4】設(shè)集合M={x|x2+2(1-a)x+3-a≤0,x∈R},集合B={x|-1≤x-1≤2},若M?B,求實數(shù)a的取值范圍. 【評注】本題集合A是不等式x2+2(1-a)x+3-a≤0的解集[x1,x2],實質(zhì)上就是函數(shù)f(x)的函數(shù)值小于0時對應(yīng)的x的范圍,在圖形上表現(xiàn)為圖象位于x軸下方的自變量的范圍,[x1,x2]?[0,3],就是在區(qū)間[0,3]上f(x)的函數(shù)值都不大于0. 【變式4】設(shè)集合M={x|x2+2(1-a)x+3-a≤0,x∈R},集合B={x|1≤x≤3},若M?B,求實數(shù)a的取值范圍. 或-1 【評注】這類問題適合用補集思想,即先求2∈M時a的取值范圍再取補集即可.法2 中容易遺漏4a-1<0(即M=?)這種情況. 【評注】注意只有一個子集與只含有一個元素的區(qū)別.單元素集合有兩個子集,而空集只有一個子集. ( ) A.4________B.3________C.2________D.1 【解析】由題意,A∩B為單元素集,即雙曲線x2-y2=1與y=t(x+2)+3有且僅有一個交點,則y=t(x+2)+3為雙曲線切線(有兩條)或與漸近線平行(有兩條),所以對應(yīng)t值的個數(shù)為4,故選A. (作者單位:山東省濱州市鄒平縣黃山中學(xué))二、用數(shù)軸處理兩個集合存在公共元素的問題

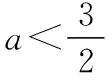
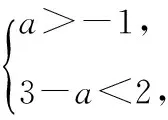
三、 韋恩圖(Venn圖)的應(yīng)用
四、函數(shù)圖象處理集合之間的包含關(guān)系
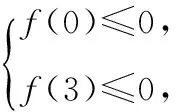
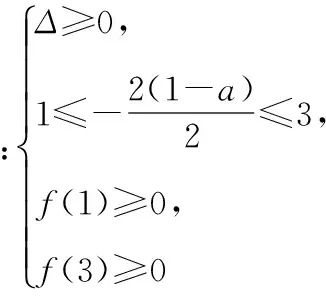
五、元素不屬于集合的兩種處理方式
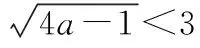
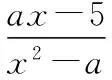
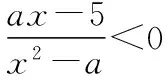
六、單元素集合與集合的子集只有一個的問題