基本不等式的兩種特殊應用
——例談“1”的代換

安徽 郭洪莉

(作者單位:安徽省蚌埠市懷遠三中)

基本不等式的兩種特殊應用
——例談“1”的代換

利用基本不等式在求函數最值、求參數范圍是高考的熱點，深刻理解基本不等式以及會使用基本不等式是學生學習中的重點.本文就著重介紹運用基本不等式求代數式的最值類型中的兩種特殊應用以饗讀者.

一、 “1”的代換

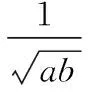
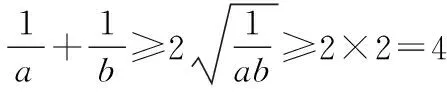
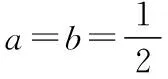
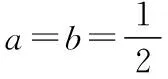
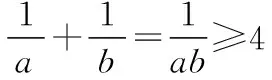
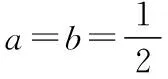
(法3)∵a,b>0,a+b=1，

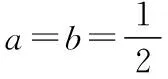
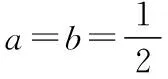
【評注】上述法1、法2都是兩次使用了基本不等式，不等號也能同時成立，符合不等式傳遞性，求出來的最小值也是正確的，但是卻不是此類問題的通法，因為等號成立的條件很脆弱，當已知條件稍微修改，如a+3b=1，那么等號成立的條件就喪失了；法三則只是用一次基本不等式，等號又能取到，不會出現法1、2的尷尬，是一個通法．

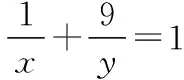
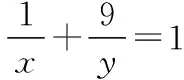
【評注】本題定值是以分式形式出現，目標函數則是整式.那么這里的“1”代到哪里去呢？顯然是代到x+y的旁邊，并與之相乘，即(x+y)ד1”.此種方法有人把它稱為“1”的附乘．凡是定值不為1也可這樣用，這種方法也經常用，此類題型同樣是具體有如下特點：分式的分母之和往往與多項式相差一數．

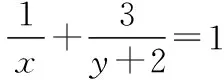
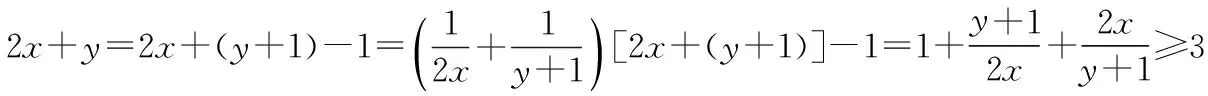
當且僅當x=1,y=1時等號成立，

所以2x+y的最小值為3.

3 . 分母之和為常數是用“1”的代換的特征

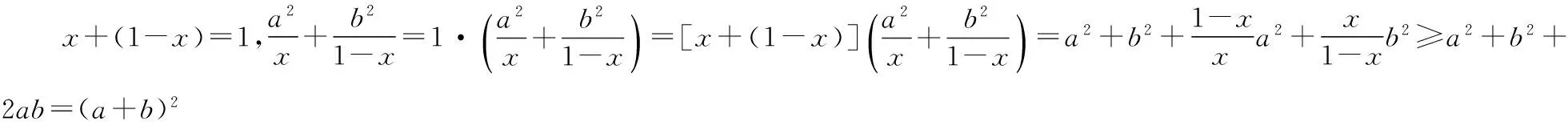
【評注】本題要注意分式的分母x,1-x的整體特點，從而探索到隱含的條件：和為定值即x+(1-x)=1.

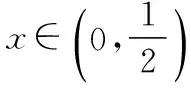
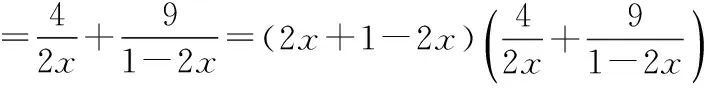
4.曲線過一點,為“1”的代換提供“定值”

【評注】對于一些結構復雜的的函數式，可以采用換元法，使得它們的特征“分母之和為定值”更加顯現.

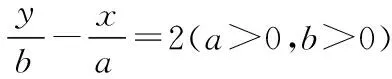
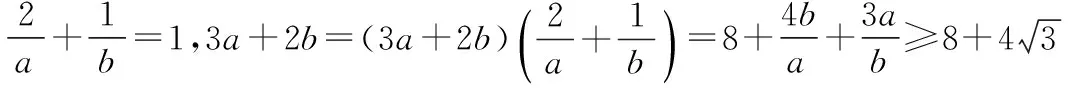
5. 隱藏在三角最值中的“1”的代換

【評注】“1”的代換的形式特征是分式的分母相加，可得到定值．分母相加，平方關系sin2x+cos2x=1，等，都可能提供分母之和為定值的條件．

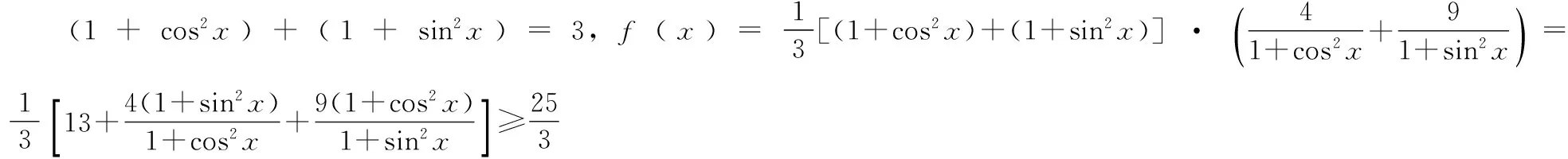
二、似曾相識的“1”的代換

1.換元法可凸顯“1”的代換的典型特征

【評注】待求式的分母較為復雜，研究雙變元分式函數的最值問題，常用換元法.

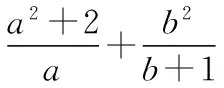
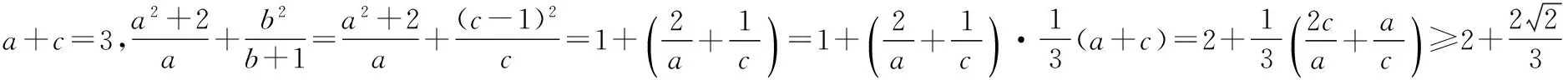
2.含有不等關系m+n≤a的“1”的代換

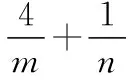
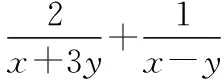
3.“1”的代換在不等式恒成立中的應用

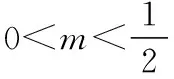
【評注】通過對原不等式的變形，最終化歸成典型的“1”的附乘問題.

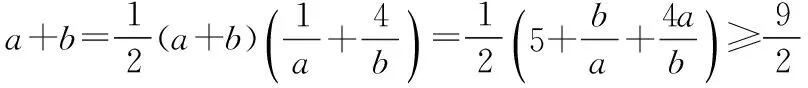
4.“1”的代換在數列最值中的應用

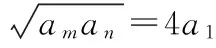
【解析】由a3=a2+2a1，可得q2-q-2=0，

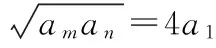
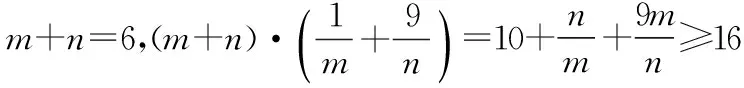
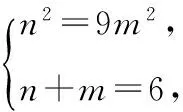
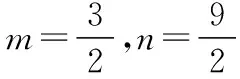
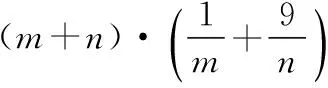
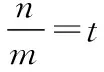
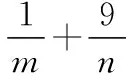
【評注】均值不等式與數列知識交匯也是近年高考常考題，仍然是先求出和或積的定值，再用均值不等式，但要特別注意m，n為正整數這一條件，要細心考察等號是否成立.

(作者單位:安徽省蚌埠市懷遠三中)