小題大做，別有洞天
——解決向量問題需要強化的五種意識

吉林 林逸凡

(作者單位：吉林省長春市吉林大學附中實驗學校)

小題大做，別有洞天
——解決向量問題需要強化的五種意識

向量問題靈活性強，活躍在各地的高考題、模擬題的選擇、填空壓軸題中，許多學生一直都是“想說愛你不容易”，本文以一道小題為例，總結(jié)解決向量問題需要強化的五種意識.

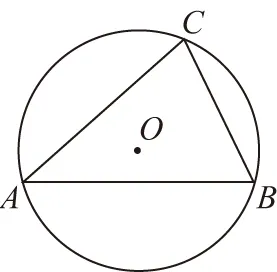
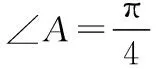
意識一：取基底

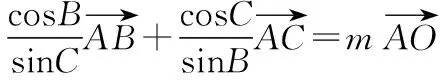
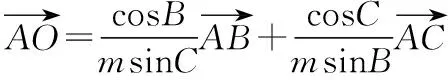
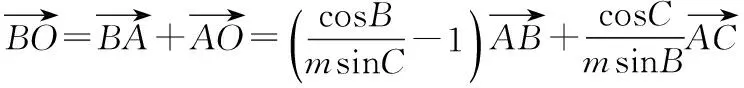
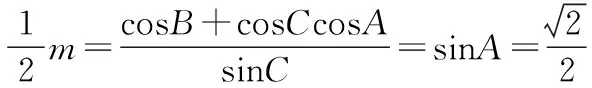
【點評】方法一的核心思想是“基底化”，優(yōu)點是通用性強，缺點是計算量較大.選取兩個不共線的向量為基底，則平面內(nèi)所有向量都可以表示為這兩個向量的線性組合.這個方法同樣適用于解立體幾何問題，只需選取兩兩不共線的三個向量為基底即可.

( )

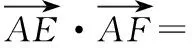
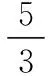
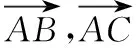
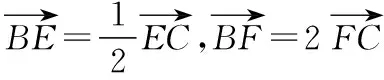
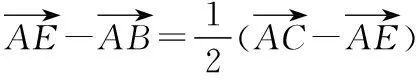
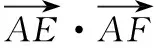
意識二：等式兩邊同時點乘一個向量，構(gòu)造數(shù)量積

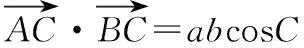
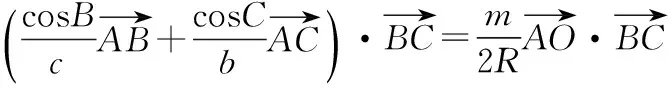
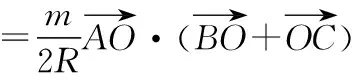
而∠AOB=2∠C,∠AOC=2∠B，OA=OB=OC=R，

將①②代入③可得

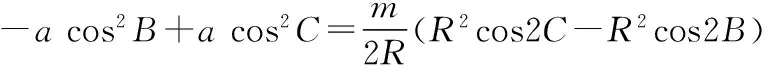
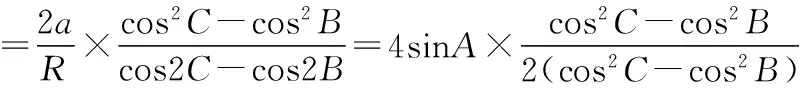
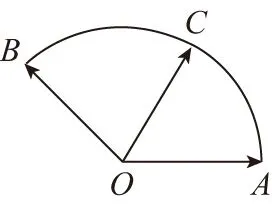
【解析】設∠AOC=α，

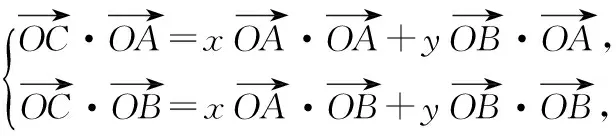
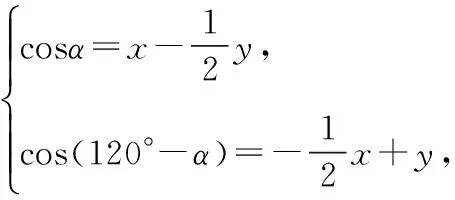
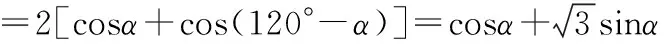
意識三：數(shù)形結(jié)合

【解法3】當cosB>0,cosC>0時，

如圖，作平行四邊形AEFD，

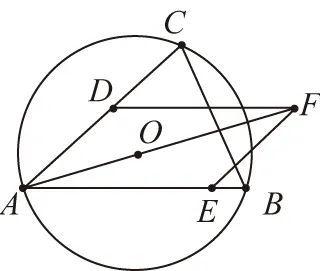
使AD=cosB,AE=cosC，

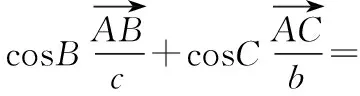
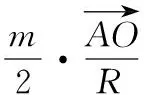
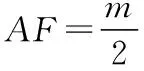
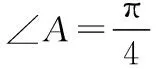
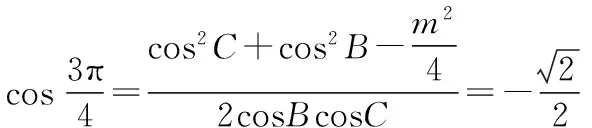
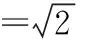
當cosB<0,cosC>0時，

如圖，作平行四邊形AEFD，

使AD=-cosB,AE=cosC，

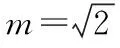
當cosB>0,cosC<0時，同理可得.

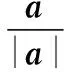
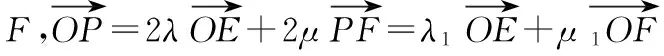
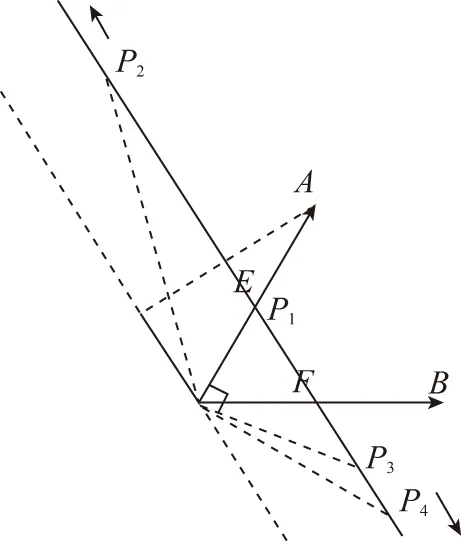
意識四：先“拆”再“合”

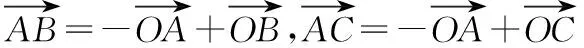
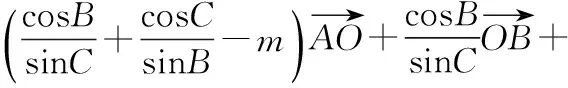
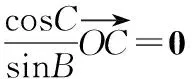
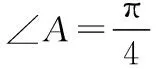
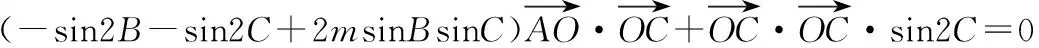
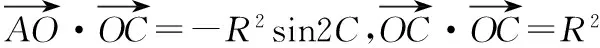
所以由②式可得-sin2B-sin2C+2msinBsinC=1，

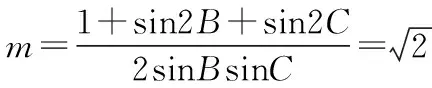
【點評】方法四本質(zhì)也是基底化的思想，與方法一有類似之處，只是不忙取基底，而是“先拆再整”：先“拆”，將向量拆成若干個特定向量的線性組合，再“合”，利用特定向量間的關系，化簡式子.

( )

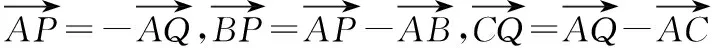
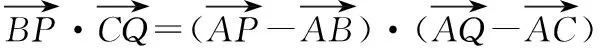
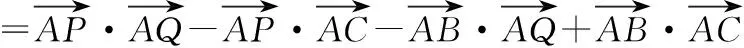
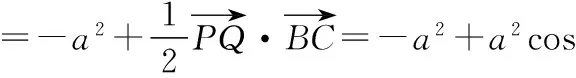
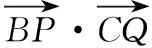
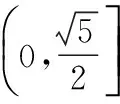
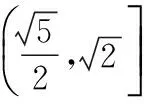
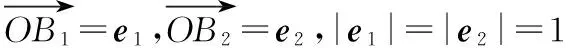
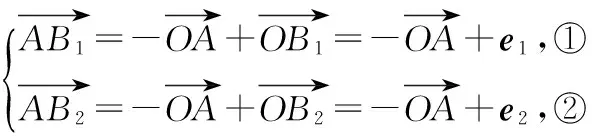
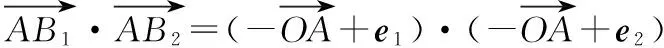
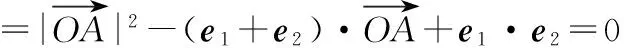
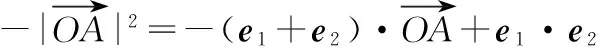
又由①②得

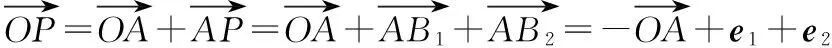
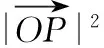
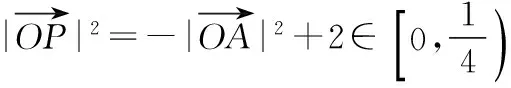
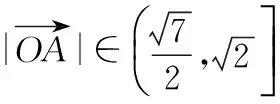
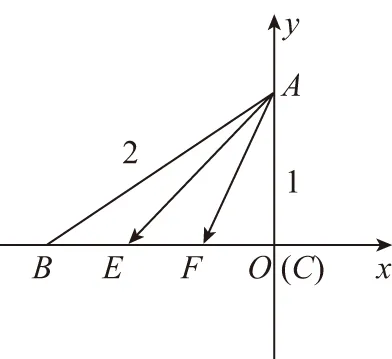
意識五：建系

【思路】建系設點，通過將向量坐標化解決.

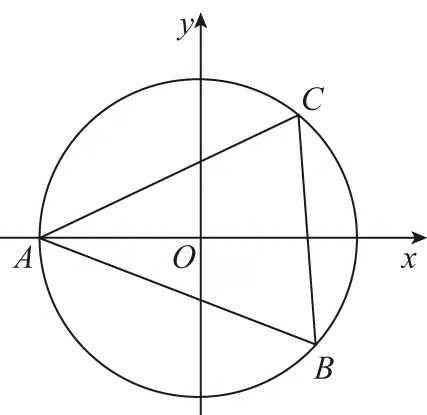
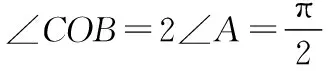
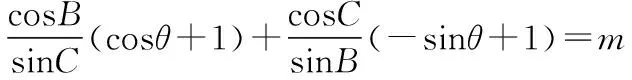
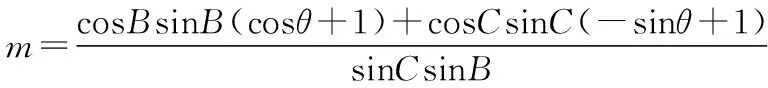
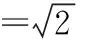
【點評】方法五的建系思想是常見且具有通用性的，在沒有靈感的時候，只要建系建對，設點設好，理論上用建系的方法一定能解出來，在解決很多數(shù)量積的最值問題時，建系是一個不錯的選擇.

【變式5-1】同【變式4-2】.

【解析】如圖，建立以A為坐標原點的直角坐標系，

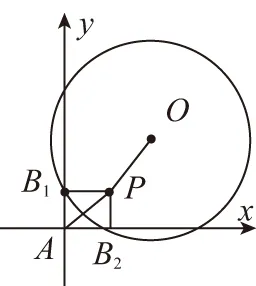
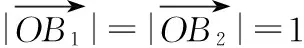
∴過點B1,B2作一個半徑為1的單位圓，圓心為O(a,b).

設B1(0,y),B2(x,0)，

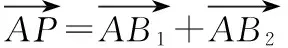
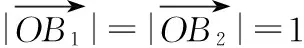
得(x-a)2+b2=1,a2+(y-b)2=1，

兩式相加得(x-a)2+(y-b)2+b2+a2=2，

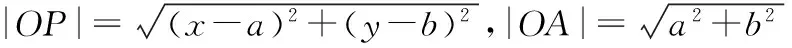
∴|OP|2+|OA|2=2，

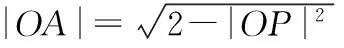
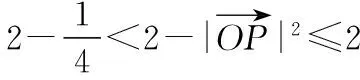
【變式5-2】同【變式1】.

【解析】由∠BAC=60°，AB=2，AC=1

可得∠ACB=90°，如圖,建立直角坐標系，

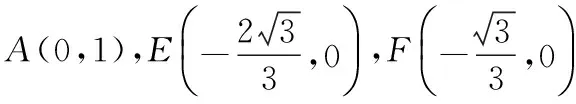
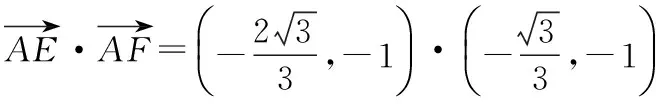
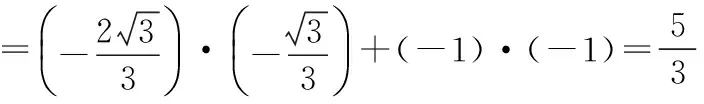
(作者單位：吉林省長春市吉林大學附中實驗學校)