研究數列有三法
——列舉觀察與歸納

湖北 盧曉勇

(作者單位：湖北省孝感市云夢縣黃香高級中學)

研究數列有三法
——列舉觀察與歸納

研究、認識數列的最簡單的方法就是列舉，列舉出足夠多的項，然后觀察、實驗、猜測、歸納、類比、抽象、概括，尋找出最本質的東西，進而就能發現規律，找到解題的基本方向.

1．觀察數列規律，寫出通項公式

【例1】已知數列{an}的前幾項，寫出它的一個通項公式．

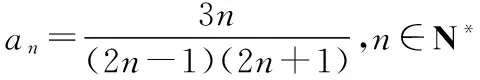
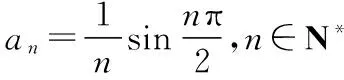
(3)每項的分母為2n的形式，從第2項起每項的分子比分母小3，且正負相間.

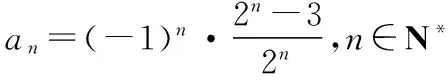
【評注】觀察法求數列的通項公式，根據數列的前幾項求通項公式時，抓住以下幾方面的特征：①分式中分子、分母的特征，分子與分母的差異特征；②相鄰項的變化特征；③拆項后的特征；④各項符號的特征．聯想項與序號n的函數關系．

如果給出的項中既有分數又有整數的統一化為分數即一定要統一形式，有些分數進行了約分，還要再進行還原； 如果有正有負的可以用(-1)n或者(-1)n+1調整，也可以利用三角函數調整．

【變式】寫出數列的一個通項公式，使它的前4項分別是下列各數：

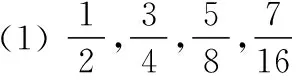
(2)9,99,999,9 999;

(3)-1,2,-3,4；

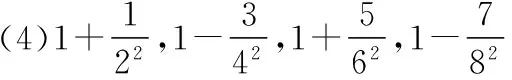
(5)3,15,35,63.

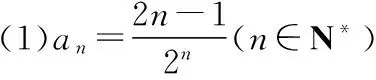
(2)an=10n-1(n∈N*)；

(3)an=(-1)nn(n∈N*)；

(5)an=(2n-1)(2n+1)=4n2-1(n∈N*).

2. 觀察圖形,總結通項公式

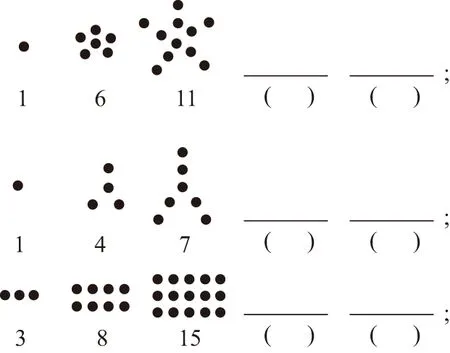
【例2】(1)根據下面的圖形及相應的點數，在空格和括號中分別填上適當的圖形和點數，并寫出點數構成的數列的一個通項公式：

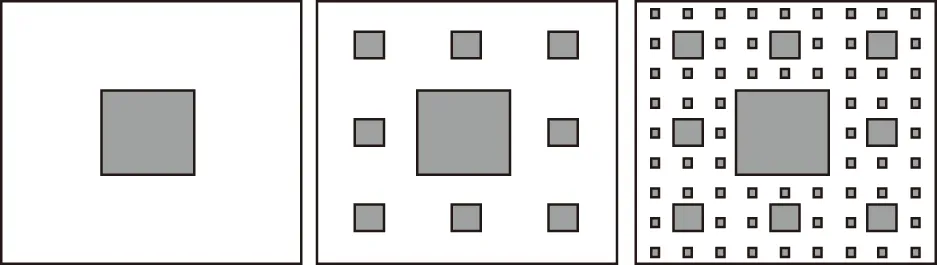
(2)下圖中的三個正方形塊中，著色正方形的個數依次構成一個數列的前3項．請寫出這個數列的前5項和數列的一個通項公式.

【解析】(1)①16，21，an=5n-4 (n∈N*)；

②10,13,an=3n-2 (n∈N*)；

③24,35,an=n2+2n(n∈N*).

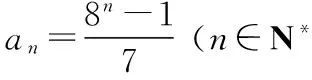
【評注】觀察圖形求數列的通項公式，根據圖形前幾項求通項公式時，抓住以下幾方面的特征：①圖形發展變化的規律；②相鄰項的變化特征；③建立數列遞推關系式求解.

【變式】把正整數按一定的規則排成了如圖所示的三角形數表．

1

2________4

3 5 7

6 8 10 12

9 11 13 15 17

14 16 18 20 22 24

設aij(i,j∈N*)是位于這個三角形數表中從上往下數第i行、從左往右數第j個數，如a52=11.則a87=________.

【解析】由三角形數表可以看出其奇數行為奇數列，偶數行為偶數列，故a87表示第8行的第7個數字，即第2+4+6+7=19個正偶數．故a87=2×19=38.

3.列舉法是研究項的最簡單方法

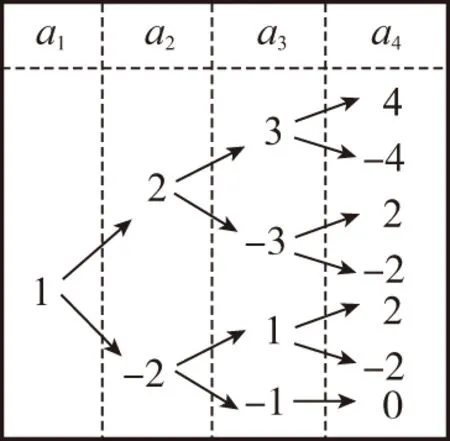
【例3】在數列{an}中，a1=1,|an|=|an-1+1|(n≥2,n∈N*)，則a1+a2+a3+a4的最小值是________.

【解析】可用樹狀圖分析，得滿足條件的數列共有7個，易得a1+a2+a3+a4的最小值是-2.

4.有些數列的項具有周期性

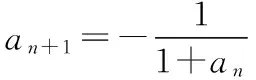
所以數列{an}的周期T=3，

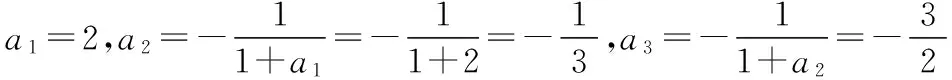
【評注】若有f(x+T)=f(x)，則f(x)的周期是T．類似地，若an+k=an(n∈N*,k為非零正整數)，則{an}為周期數列，T=k為{an}的一個周期．

【變式】已知數列{an}滿足a1=1,a2=1,an+1=|an-an-1|(n≥2)，則該數列前2 012項和等于________．

【解析】因為a1=1,a2=1,an+1=|an-an-1|(n≥2)，所以a3=|a2-a1|=0;a4=|a3-a2|=1;a5=|a4-a3|=1;a6=|a5-a4|=0,…,

所以數列{an}是周期為3的數列，每個周期內所有項的和為2，

【例5】在數列{an}中，已知a1=2,a2=3,當n≥2時，an+1是an·an-1的個位數，則a2016=________.

【解析】因為a1=2,a2=3,

所以a3=6,a4=8,a5=8,a6=4,a7=2,a8=8,

a9=6,a10=8,a11=8,a12=4,a13=2,a14=8,…,

所以數列{an}從第3項起是以6為周期的數列，

因為2 016=2+335×6+4,

所a2016=a2+4=a6=4.

【評注】函數周期是T，則f(x+kT)=f(x),k∈Z，類似地，若數列周期是T，則am+kT=am(其中m∈N*,k∈N,T為非零正整數)．尋找數列的周期，可以先通過列舉的方法進行．

【變式】已知數列{an}中，Sn是其前n項和，若a1=1,a2=2,anan+1an+2=an+an+1+an+2，且an+1an+2≠1，則a1+a2+a3=________，S2010=________．

(作者單位：湖北省孝感市云夢縣黃香高級中學)