一道圓錐曲線高考題的探索歷程

安徽 劉 陽

(作者單位：安徽省阜陽市太和中學)

一道圓錐曲線高考題的探索歷程

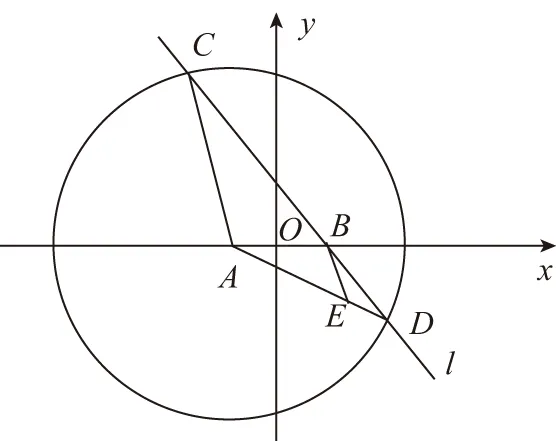
【例題】(2016·新課標Ⅰ理·20)設圓x2+y2+2x-15=0的圓心為A，直線l過點B(1,0)且與x軸不重合，l交圓A于C，D兩點，過B作AC的平行線交AD于點E.

(Ⅰ)證明|EA|+|EB|為定值，并寫出點E的軌跡方程；

(Ⅱ)設點E的軌跡為曲線C1，直線l交C1于M,N兩點，過B且與l垂直的直線與圓A交于P,Q兩點，求四邊形MPNQ面積的取值范圍.

一、考點分析

(1)考點、熱點的考查：直線、圓和橢圓.

(2)能力和應用意識的考查：邏輯推理的能力、運算求解的能力、數(shù)據(jù)處理的能力、數(shù)形結合應用意識和設而不求應用意識.

二、審題分析

采取化整為零，步步為營的策略.

(1)“圓x2+y2+2x-15=0的圓心為A”，將這句話“翻譯”為：“圓A的標準方程為(x+1)2+y2=16,圓心A(-1,0)”;

(2)“直線l過點B(1,0)且與x軸不重合，l交圓A于C，D兩點”，這句話表明直線l不與y軸垂直，這句話間接告訴考生此條件將為問題的解決隱含著什么；一是動直線l方程的兩種設法，二是求點E的軌跡方程y隱含條件埋下伏筆；

(3)“過B作AC的平行線交AD于點E”，此處會讓考生聯(lián)想平行線的性質定理和三角形相似性——在三角形中平行與一邊的直線將原三角形形成兩個三角形相似，同時由線段AC和線段AD都是圓A半徑，得出△ACD為等腰三角形；

(4)“證明|EA|+|EB|為定值，并寫出點E的軌跡方程”，此問又含有兩小問：先證定值、接著根據(jù)定值判定軌跡曲線類型再書寫軌跡方程，要注意書寫方程根據(jù)點E的軌跡帶上y的限制條件；

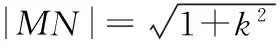
三、解題分析

【解】(Ⅰ)因為|AD|=|AC|,EB∥AC,

故∠EBD=∠ACD=∠ADC，所以|EB|=|ED|,

故|EA|+|EB|=|EA|+|ED|=|AD|，如下圖.

又圓A的標準方程為(x+1)2+y2=16，

從而|AD|=4，所以|EA|+|EB|=4.

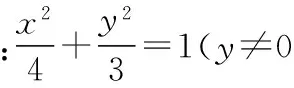
(Ⅱ)當l與x軸不垂直時，設l的方程為y=k(x-1)(k≠0),M(x1,y1),N(x2,y2).如下圖.

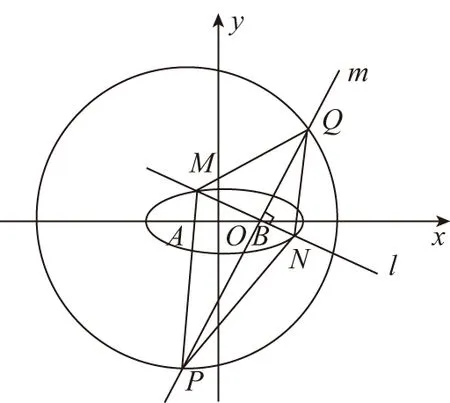
由題知Δ>0顯然成立，

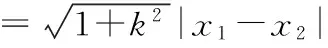
過點B(1,0)且與l垂直的直線m：

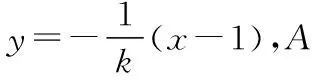
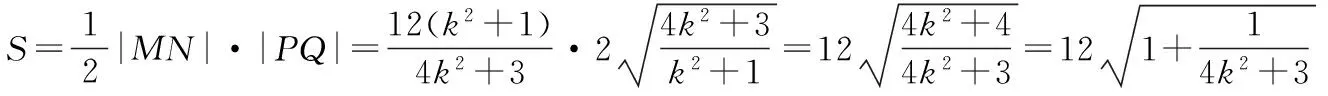
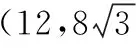
當與x軸垂直時，其方程為x=1，|MN|=3，|PQ|=8，四邊形MPNQ的面積為12.

又AC=AD,∴BE=DE，以下相同.

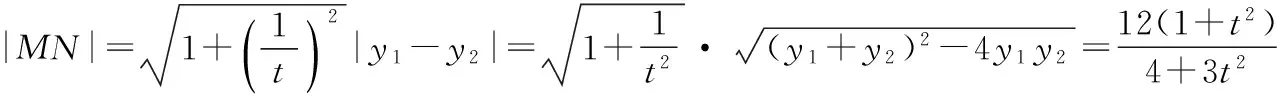
直線l的方程可化為：x-ty-1=0,t∈R,

直線m方程可以設為tx+y+c=0,

把B(1,0)代入得c=-t,

∴直線m方程：tx+y-t=0.

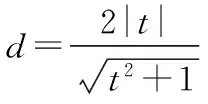
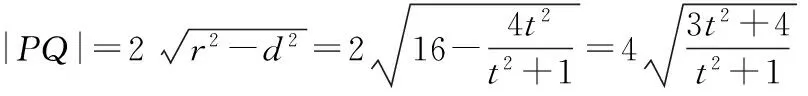
四、變式分析

(1)求橢圓的標準方程；

(2)過橢圓的右焦點F作直線l1,l2,直線l1與橢圓分別交于M，N點，直線l2與橢圓分別交于P，Q點，且l1⊥l2，求四邊形MPNQ的面積S的最小值.

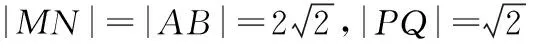
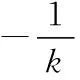
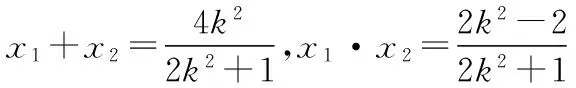
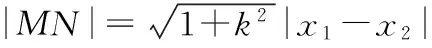
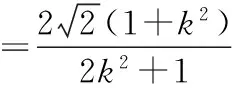
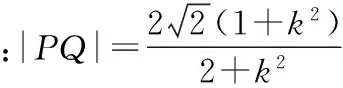
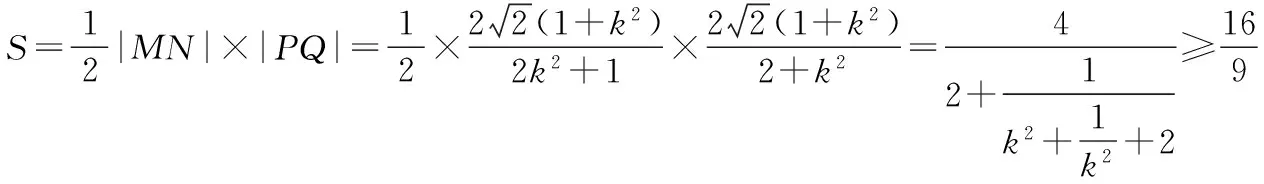
當且僅當k=±1時等號成立.

求四邊形ABCD的面積的最小值.

【解析】(1)若直線BD的斜率k=0或斜率不存在時，四邊形MPNQ的面積S=4.

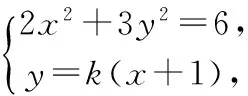
設B(x1,y1),D(x2,y2)，

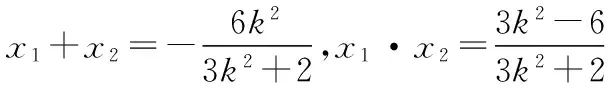
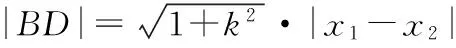
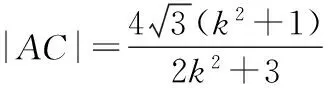
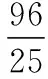
(作者單位：安徽省阜陽市太和中學)