由淺入深，逐步培養學生抽象概括能力

陳湘芬

思維能力是人的認識能力（即智力）的核心，而抽象概括能力是其中的重要組成部分。然而，當前教學中經常遇到的情況是：學生對具體、形象、鮮明的內容比較感興趣，對抽象的內容不易接受。

如何提升學生的抽象概括能力呢？現以北師大版《數學》五年級下冊《包裝的學問》一課為例，談談個人的教學體會。

一、從表象開始，逐步抽象

表象是連接感性認識和理性認識的橋梁。要培養學生的抽象思維能力，教師首先在教學中要引導學生學會逐步抽象，重視表象在形象思維向抽象思維上升過程中的作用。運用觀察、操作、實驗等多種形式，調動學生多種感官參與感知，指導學生用抽象的方法解決問題。

活動一：包糖果

六一節快到了，教師在準備禮時想把兩盒同樣大小的糖果包成一包，怎樣包才能節約包裝紙？（接口處不計，單位：cm）

1.議一議

師：看到這個問題，說說你是怎么想的？

生1：要節約包裝紙，就要使兩包糖果拼起來的表面積最小。

生2：可以用學具拼一拼，看看哪種包裝方法表面積最小。

生3：還可以看看哪種包裝方法重疊部分面積最大。

……

2.拼一拼

兩盒糖果包成一包，可以怎樣包？有幾種不同的方案？

同桌合作，動手拼一拼，弄清幾種不同的包裝方案。

3.算一算

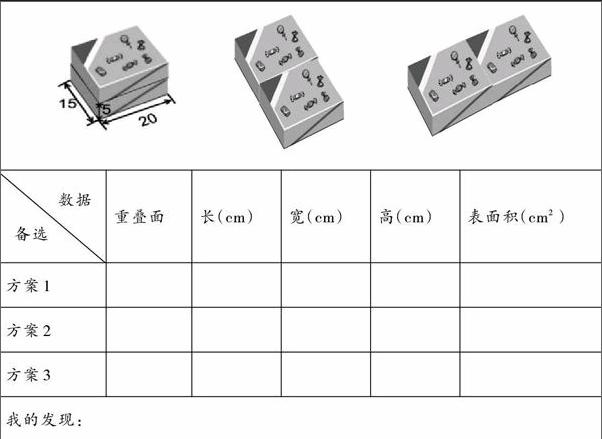
如圖，你能計算出哪一種方案最節約包裝紙？想一想、填一填。

4.學生獨立計算，反饋匯報，交流自己的發現

在這一活動中，學生不難發現，包裝兩盒糖果，拼成長方體后表面積有3種不同情況，重疊面越大，表面積越小。

簡單的包裝拼接游戲，讓學生通過動手操作找到解決問題的途徑。接著，又讓學生整理歸類完成表格，再觀察比較說說自己的發現。這樣，就讓學生從表象開始，逐步培養抽象概括的能力。

二、重比較類推，建構抽象

數學的完整性和嚴密性，使得數學結論和方法都具有相關性和相似性。在課堂教學中教師要充分利用這些相關性和相似性，注重類比聯想，讓學生自己探索和發現許多新的結論或方法，再通過發掘新知識的相同點或相似點進行類比和推理，從而實現知識的遷移和方法的創新，逐步形成抽象思維能力。

活動二：包磁帶

1.將四盒磁帶（長，110mm；寬，70mm；高，16mm）包成一包，你能想出幾種包裝方法？可以先畫出草圖，再在小組內進行交流。

2.說一說自己的想法。

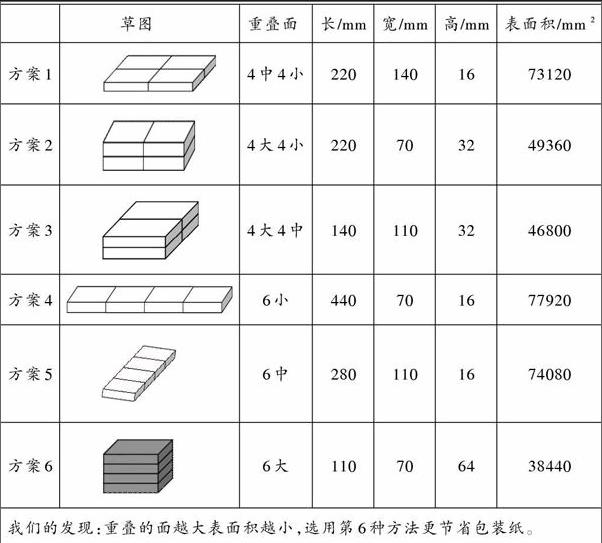
3.小組合作算一算、填一填，哪一種方案最節約包裝紙？你有什么發現？

學生分析比較后，反饋匯報：6個大面重疊時，更節省包裝紙。如下表：

4.交流體會

對照這些數據和我們的思考過程，你有什么想法？

學生發現：將一盒長方體磁帶的長、寬、高分別看成單位1，無論哪種包裝，新長方體的總體積一定（長×寬×高=4），而且6種包裝法分別是4=2×2×1；4=2×1×2；4=1×2×2；4=4×1×1；4=1×4×1；4=1×1×4。

本活動中，學生發現，包裝4盒磁帶，表面積出現了6種不同情況，包裝多個相同的長方體，方案有多種，把面積最大的面重疊起來，最節約包裝紙，也便于攜帶。每一個方案都讓學生切實體驗到了知識的獲得過程，又在比較歸納中發展了抽象概括能力。

三、重應用檢驗，深化抽象

“知識不等于能力，能力生發于實踐。”數學教學中要實現數學知識的有效遷移、同化，還需要引導學生回到學習中去應用檢驗。

活動三：包更多物品

如果有更多的長方體磁帶盒（出示12盒磁帶）進行組合包裝，猜猜是不是也像剛才一樣，只要大面重疊就最節省包裝紙呢？下面動手操作驗證猜想。

1.要求：小組合作，拼一拼，拼完后，請組長展示你們組認為最節省包裝紙的拼法。

2.反饋討論：

（1）說一說，你們組有幾種不同的拼法？展示你們組認為最節省的拼法？

（2）算一算，算出最節約的拼法減少的面積？

（3）想一想，為什么這樣拼最節約？

3.交流體會

每次操作完后，筆者組織學生進行討論、歸納規律。當磁帶盒增加到12個時，有15種拼法。受之前拼4盒磁帶盒的影響，學生認為大面重疊最節省包裝材料，卻忽略了排兩排更節約，又便于攜帶。當長、寬、高三個數最接近時，即它們相加的和最小的時候，表面積最小。最后，學生發現：考慮不同包裝方案，可以從“長×寬×高”入手尋找，做到有序思考。

通過比較辨別、應用檢驗，讓學生充分發揮團隊精神進行小組合作探究，感受到了思考問題時要注重多角度、有序思考，從而充分培養學生優化思維和求異思維，訓練了學生的空間思維，深化了學生的抽象概括能力。

四、重活動延伸，升華抽象

抽象概括過程是認清數學對象的本質，從感性上升到理性的過程，它貫穿于數學學習與教學過程的始終。因此，教師要重視拓展活動，讓學生回歸生活，在社會實踐中類比、歸納、猜想、推理，從而升華他們的抽象概括能力，使他們學會發現并總結數學規律。

活動四：設計新包裝

師：今天我們探究了《包裝的學問》，你有哪些收獲？還有疑問嗎？

（引導學生反思學習活動的價值）

師：請你們留心生活，看看超市里哪些商品的組合包裝比較特別？想想廠家為什么這樣包裝？你能為它的包裝設計新方案嗎？

生活是數學實踐和創新的源泉，只有讓學生回歸生活，在真正的社會實踐活動中去感受，才能打破思維定勢，促進實踐創新。

《包裝的學問》從簡單的表象開始，讓學生逐步接觸抽象概括，并夯實了“類比推理”與“應用檢驗”這兩個重點環節，最后還布置了一個創新性的實踐活動。這樣的教學雖然很費時間，卻抓住了“由淺入深培養學生抽象概括能力”這一關鍵。數學的學習不能僅僅讓學生被動吸收教材知識，更要讓學生主動參與、親身實踐，充分發展抽象概括能力。