淺析西方媒體關于中拉關系報道的議題設置
楊春雪+崔元磊
黨的十八大以來,中國的發展進入新的戰略機遇期,在國際政治經濟舞臺上發揮越來越重要的角色。與此同時,中國卻面臨著“修昔底德陷阱”(新興大國必然會挑戰現有大國,遏制與反遏制最終必然通過戰爭解決)的威脅①。這一陷阱在新聞傳播領域則表現在,西方媒體通過極端地強化媒體的“議題設置”功能,來引導國際輿論,從而達到對中國形象的片面解讀,甚至歪曲、抹黑的目的。
面對中國的崛起,中國對外交往的擴大,西方媒體通過對報道角度、新聞焦點、新聞取景框架、事實以及信源的選擇②,在很大程度上影響著公眾看問題的立場和觀點,也在一定程度上助長了“中國威脅論”的論調。以中國和拉美國家的關系為例,五年來,中國國家主席習近平三訪拉美地區,中拉關系在經貿、文化等領域實現了跨越式發展。但西方媒體卻通過議題設置,試圖扭轉現實,將“中國威脅論”的論調在讀者心中不斷強化。本文通過在谷歌搜索中輸入“China, Latin America”,選取了2016年1月至2017年3月期間十四篇西方主流媒體關于中拉關系的報道,嘗試對西方媒體的議題設置和實現手法進行分析。
一、議題設置之主題設置
在選取的報道中,有些是評論性報道,刊登在該媒體的評論專欄里;另一些則是基于事實的客觀報道。然而,筆者發現,無論是哪一種類型的報道,文章都或明或暗地進行了相同的議題設置——即把中拉關系的友好發展政治化、野心化。如表一所示,西方媒體議題設置的主題在文章標題中一目了然。
筆者發現,在這些報道中,西方媒體對中拉關系的議題設置歸根結底在“中國威脅論”上——中國同拉美關系的友好發展,一方面是對拉美經濟的威脅,另一方面是對美國的威脅。在上述報道中,西方媒體將這兩種威脅細化,設置了眾多分議題。其中,有關中國對拉美威脅的攻擊論點有三,主要集中于經濟領域:一是中國在拉美地區開發資源,破壞當地生態環境;二是大量廉價的中國制造的商品進入拉美地區,掏空當地的制造業,使其經濟發展更加依賴于原材料的出口;三是隨著中國經濟的增速放緩,在經濟上依賴中國的巴西、智利等國陷入經濟危機。對美國的威脅則集中于中國“別有用心”的地緣政治目的。有些報道還指明中國此舉旨在“美國后院”組建反美勢力,并暗示中國對此蓄謀已久,在美國近來對拉美地區放松警惕之時“趁虛而入”。
西方媒體圍繞著“中國威脅論”的總體議題,源源不斷地設置新的分議題,試圖以此來塑造中國“不負責任”的大國形象。久而久之,西方媒體制造的“第二手現實”則易深入人心。
二、議題設置之實現手法
除了在文章的主題上下功夫,西方媒體還在文章的采訪、寫作過程中煞費苦心,小到一個單詞,大到整個段落,以圖更好地佐證其設置的議題。通過對信息的取舍、轉述和組合,西方媒體將預設的觀點和立場隱藏于字里行間,讓文章顯得有理有據。
1.選擇“恰當”詞語
單詞是文章構成的基本單位。西方媒體為了更好地實現議題設置,在基本單位的選擇上十分考究。例如,《華爾街日報》在文章《中國進一步聚焦拉丁美洲》中選擇用“expansion”一詞來描述中國的對外關系。該詞在經濟領域有增長、發展之意,但在政治領域往往指擴張。文章四次使用該詞談及中國,在此列舉兩句:
There is little internal debate in the Communist Party around the merits of global expansion…(共產黨內部對于全球擴張的好處沒有爭議……)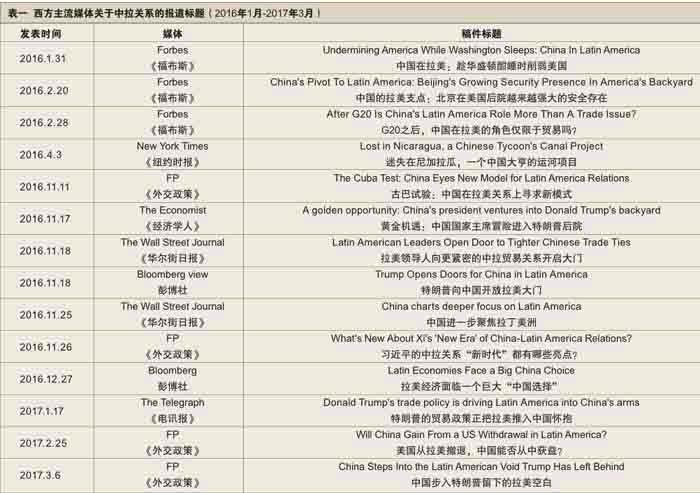
With the expansion came the same criticism Beijing has faced in Africa…(伴隨擴張而來的是跟北京在非洲一樣受到的批評……)
“expansion”一詞的多次運用則潛移默化地引導讀者將中國對拉美的友好關系視為一種政治上的擴張。西方媒體通過對詞語的選擇,將主觀偏見安插在文章適當的位置,力求在細微之處與其議題設置相呼應。
2.選取“有用”信息
為了使議題設置顯得客觀、可信,西方媒體通過信息篩選,將對其有用的信息匯總、整合。例如,下文段落選自《經濟學人》文章《黃金機遇:中國國家主席冒險進入特朗普后院》,是西方媒體典型的寫作套路:
Almost all imports from China are cheap manufactures. Some Latin American economists argue that Chinese subsidies to their producers undermine domestic industries. A new study published by the Atlantic Council, a think-tank in Washington, concludes that Chinese exports “have had an effect on the regions deindustrialisation”. As for Chinas push to invest in infrastructure and natural resources, “that wont give us the quality jobs we need,” said Rebecca Grynspan, the secretary-general of the Ibero-American Community, which comprises Spain, Portugal and Latin America, at a seminar in Santiago last week.endprint
(幾乎所有進口自中國的產品都是廉價的。一些拉美經濟學家認為中國對生產者的補貼會削弱拉美國家的工業。美國智庫大西洋理事會發表的一項新研究成果表明,中國的出口“對該地區的非工業化產生了影響”。關于中國對當地基礎設施和自然資源的投資,伊比利亞美洲共同體組織秘書長蕾維卡·格林斯潘在上周于圣地亞哥舉行的研討會上說,“這不會給我們提供優質的就業機會”,該組織由西班牙、葡萄牙和拉美國家組成。)
仔細分析這段話,第一、二句先是用“一些專家認為”來包裝、闡明觀點,該觀點指向中國對拉美經濟的威脅,緊貼整篇文章的中心議題。緊接著,作者找了一項新研究來佐證自己的觀點。這還不夠,為了讓讀者更加信服,文章又采訪了對中國抱有偏見的專家,通過“借嘴說話”再次印證前文觀點。
這種“觀點+例證+借嘴說話”的模式在西方媒體報道中極為常見。主觀觀點之后緊跟著例證和直接引語以彰顯客觀性,讓整個段落看起來有憑有據。至此,主觀和客觀之間的界限在讀者腦海中開始模糊,西方媒體便成功地將議題設置的觀點變成“第二手現實”呈現給公眾。
3.用“華麗”寫作手法混淆視聽
西方媒體報道有時還巧妙地將議題隱藏在華麗的寫作手法之下,鼓勵讀者透過表象發掘議題,以達到混淆視聽的目的。
在這方面,《紐約時報》常常技高一籌。它往往以特稿寫作的形式,加之大量的細節描寫,牽引讀者層層深入其預設的中心議題。例如,文章《迷失在尼加拉瓜,一個中國大亨的運河項目》講的是一個中國商人在尼加拉瓜開發運河項目,其開篇第三段中這樣寫道:
Three times as long and twice as deep as the Panama Canal, it would slice 170 miles across the southern part of the country — bulldozing through fragile ecosystems, virgin forests and scenes of incredible beauty. It would allow for the passage of the worlds largest ships, vessels the length of skyscrapers that are too big for the Panama Canal.
(該運河長度是巴拿馬運河的三倍,深度是其兩倍,它將在該國南部橫切170英里——推土機將經過脆弱的生態系統、原始森林和令人難以置信的美麗秘境。它將允許世界上最大的船只通過,這些船只的長度跟摩天大樓的高度一樣,這是巴拿馬運河所容納不下的。)
這些細節描寫使運河仿佛已經呈現在讀者眼前——野心勃勃的中國人正在開發尼加拉瓜的處女地,推土機正破壞當地脆弱的生態環境。然而,這些栩栩如生的華麗描寫卻均來源于作者的臆想和猜測——后文提到,運河并未開始修建,該中國公司表示他們需要做更多的開工前研究。
其實無論后文澄清與否,這一段獨具現場感的描寫已經深深印刻在讀者的腦海中,這個未開工的運河在讀者心中已經破壞了當地美麗的原始森林。讀者帶著這種成見繼續讀文章,則很容易陷入西方媒體預設的議題中。
4.假借“觀點平衡”
為確保信息的全面、客觀、公正,新聞報道的平衡原則是不可或缺的,這也就要求媒體對新聞對象進行多元化采訪,不僅反映一方的看法,還要反映多方的見解。
西方媒體當然不會忽略這一原則。然而,它們只需在該原則上稍做手腳,就可以巧妙地回避對其議題設置無益的內容。
例如,文章《迷失在尼加拉瓜,一個中國大亨的運河項目》結尾三段寫道,尼加拉瓜當地民眾對該中國運河項目褒貶不一:
Some still hope it will lift this country out of poverty.
But in Brito and the nearby city of Rivas, those who expect to be displaced are angry. Teresa de Jesus Henriquez Delgado, 31, is one of the residents who used a stencil to paint “Go Away Chinese!” on the outside of her house.
“I will resist with all of my strength when the bulldozers come to tear down my house,” she said.“I will fight until I die. I have to for my children. They cant take this land from my family.”
(有些人依舊希望運河可以幫助國家擺脫貧困。
但是在布里托和附近的里瓦斯市,那些將因為運河修建而被迫遷走的人很生氣。31歲的德雷莎是在房屋外面涂上“中國人走開”的居民之一。
“當推土機來毀掉我的房子時,我將全力反抗。”她說,“我會戰斗,直到我死。為了我的孩子,我必須這樣做。他們休想把這塊土地從我家拿走。”)
不難發現,在這三段中的“觀點平衡”實為假平衡。因為支持聲僅僅用了11個單詞一筆帶過,既沒有采訪案例,也沒有直接引語,令人難以信服。文章則是把更多筆墨放在反對聲上——不僅采訪對象身份明確,還有言辭激烈的直接引語。
在寫作結構方面,特稿的開頭和結尾處通常最令讀者印象深刻。《紐約時報》的這篇特稿以反對聲作為結尾,最后一句悲憤的引語引人深思。文章以此巧妙地打破整篇文章的觀點平衡,將讀者的思維落點牽引到預設的議題上。
新聞并非是現實社會的“鏡子式”反映,而往往是描繪世界的框架。在國際傳播實踐中,西方媒體通過上述幾種手法設置議題,無疑會使媒介現實與真實現實之間發生更大的偏移,這種偏移如同給公眾戴上有色眼鏡,使他們不能理性、客觀地認識中國的發展。
「注釋」
①郭可、楊文睿:《新戰略期國際涉華輿情新特征和輿論引導新態勢》,《對外傳播》2016年12期。
②李希光:《新聞報道與議題設置》,《新聞與寫作》2016年11期。endprint

