函數與方程的思想在高中數學中的應用
陳少婉


函數與方程的思想是高中數學的基本思想之一,是通過建立函數或方程,運用函數的圖像、性質等去分析問題,解決問題;更重要的是產生函數或方程的方法,能上升到思想高度主動思考問題.運用函數與方程的相互轉化解決零點問題、構建函數解決不等關系問題與最值問題、利用方程的思想解決消參求值問題以及切點弦問題等等,是近年高考的熱點和重難點.下面舉例說明函數與方程的思想在高中數學解題中的應用.
一、零點問題中的函數與方程思想
函數的零點問題是近幾年高考題的高頻考點和重難點.許多函數問題要用方程的知識與方法來支持;許多方程的問題,需要用函數的知識與方法去解決.函數思想是對函數內容在更高層次上的抽象、概括與提煉,方程問題的函數視角就是利用函數的圖像、性質來研究方程的根及范圍問題.
1.1.與函數的零點或方程的根或函數圖像的交點個數問題
例題1.1.(1)已知函數y=f(x)的周期為2,當x∈[-1,1]時,f(x)=x2,那么函數y=f(x)的圖像與函數y=|lgx|的圖像的交點共有( )
A. 10個 B. 9個 C. 8個 D. 1個
綜上所述,原方程有4個實根.
點評:函數零點問題的解題思路主要有兩個方向,一是算出來,即利用方程求根,運用方程的思想求解,二是畫出來,即轉化為函數圖像與軸的交點問題或者兩個函數圖像的交點問題,運用函數的思想以及數形結合的思想求解.在解題過程中,函數與方程相互轉化.本題根據分段函數不同區間的特征,綜合運用解方程、構造函數,討論單調性等方法求解.
1.2求參數的值或取值范圍問題
例題1.2. 已知函數f(x)=|x2-1|,g(x)=x2+ax+2,x∈R,若函數h(x)=f(x)+g(x)+2在(0,2)上有兩個零點x1,x2求實數a的取值范圍.
點評:運用函數的思想轉化零點問題,構造的函數不同,解法也不同,但用到的思想方法是相同的,在解題中要注意函數與方程的相互轉化.
1.3.借助零點,考查導數探究函數的性質
例題1.3. 設函數f(x)=e2x-alnx.
(Ⅰ)討論f(x)的導函數f′(x)的零點的個數;
值范圍,體現了函數的思想.解題時要注意自變量c的取值范圍,即函數定義域的確定.
三、立體幾何中的函數方程思想
函數方程思想不僅在代數解題中發揮著重要的作用,而且在立體幾何中也有著巧妙的應用.在立體幾何的動點問題、最值問題和逆向問題中,通常要運用函數與方程的思想求解.
3.1利用函數的圖像及性質解決立幾中動點的軌跡問題
例題3.1. 如圖,動點P在正方體ABCD-A1B1C1D1的對角線BD1上. 過點P作垂直于平面BB1D1D的直線,與正方體表面相交于M,N. 設BP=x,MN=y,則函數y=f(x)的圖像大致是( )
點評:本題是一道立體幾何與函數圖像相結合的題目,主要考查了函數圖像的變化.由于題目中給出了自變量和因變量,如能求出函數解析式,問題即可獲解.因此,可根據幾何體的特征和條件分析兩個變量的變化情況,通過M,N,P作底面的垂線作出M,N在平面ABCD內的正投影,保持其長度不變,從而把空間問題平面化,建立一次函數模型.
3.2利用方程的思想解立體幾何逆向題
例題3.2. 如圖,已知四棱臺ABCDA1B1C1D1的上、下底面分別是邊長為3和6的正方形,AA1=6,且AA1⊥底面ABCD,點P,Q分別在棱DD1,BC上.
(1)若P是DD1的中點,證明:AB1⊥PQ;
(2)若PQ∥平面ABB1A1,二面角PQDA的余弦值為,求四面體ADPQ的體積.
解析:由題設知,AA1,AB,AD兩兩垂直,以A為坐標原點,AB,AD,AA1所在直線分別為x軸,y軸,z軸,建立如圖所示的空間直角坐標系,則相關各點的坐標為A(0,0,0),B1(3,0,6),D(0,6,0),D1(0,3,6),Q(6,m,0),其中m=BQ,0≤m≤6.
點評:本題是一道立體幾何逆向題.通過設定變量m,λ利用二面角PQDA的余弦值為以及PQ∥平面ABB1A1的條件建立等量關系,求出變量m,λ的值,體現了方程的思想.
3.3運用函數的思想解決立幾中的最值問題
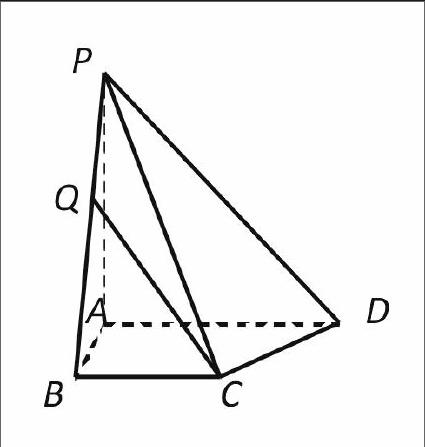
例題3.3. 如圖,在四棱錐P-ABCD中,已知PA⊥平面ABCD,且四邊形ABCD為直角梯形,∠ABC=∠BAD=,PA=AD=2,AB=BC=1.
(1)求平面PAB與平面PCD所成二面角的余弦值;
(2)點Q是線段BP上的動點,當直線CQ與DP所成角最小時,求線段BQ的長.
解析:以{,,}為正交基底建立如圖所示的空間直角坐標系A-xyz,則各點的坐標為B(1,
總之,作為高中數學基礎知識的重要內容,數學思想與數學方法屬于教學中的重點,也是學生學習過程中的難點.通過思想與方法的學習能夠真正理解數學的價值和意義.函數與方程的思想是高中數學的基本思想方法之一,也是高考的重中之中,是掌握許多數學知識的基礎. 運用函數與方程的思想方法去解題,才舉一反三,融會貫通,才能俯瞰題目,達到“一覽眾山小”的境界.函數與方程思想的運用在高中數學中無處不在,在解題中應注意體會,歸納總結,形成方法和能力.
責任編輯 徐國堅

