基于仿真的多部件系統狀態維修決策優化方法

王少華， 張耀輝， 徐隆洋， 劉宏祥

(1.裝甲兵工程學院 技術保障工程系， 北京 100072； 2.裝甲兵工程學院 科研部， 北京 100072)

基于仿真的多部件系統狀態維修決策優化方法

王少華1， 張耀輝1， 徐隆洋1， 劉宏祥2

(1.裝甲兵工程學院 技術保障工程系， 北京 100072； 2.裝甲兵工程學院 科研部， 北京 100072)

為通過部件組合維修提高維修效益，對采用狀態維修的多部件系統，建立了部件狀態隨機劣化模型。采用冪指數函數建立以狀態值為變量的可靠度函數，在考慮不完全維修、維修時間隨機分布等因素的條件下，采用蒙特卡洛仿真方法建立了系統狀態劣化過程模型。以單位壽命費用最小為優化目標，建立了多部件系統狀態維修閾值的優化決策模型。案例分析結果表明，建立的狀態維修決策優化模型能夠顯著降低維修費用、提高系統可用度，是適用且有效的。

兵器科學與技術； 狀態維修； 不完全維修； 蒙特卡洛仿真； 決策優化

0 引言

狀態維修是在裝備運行過程中，通過機內或外部檢測設備獲得裝備的狀態信息，通過狀態評估和預測得到裝備的實時狀態和發展趨勢，適時安排預防性維修的一種維修方式[1]。狀態維修能夠在降低裝備壽命周期費用的同時，有效地降低裝備故障風險，提高戰備完好性。如何利用裝備的狀態變化規律，對狀態檢測策略和預防性維修閾值進行優化，是狀態維修決策的關鍵內容[2]。對于復雜的多部件系統來說，系統狀態由其內部各部件決定，而對于部件級的維修對象，其狀態的隨機劣化過程往往是不可逆的，預防性維修往往無法使部件狀態達到“修復如新”，因此假設預防性維修為“不完全維修”。在“不完全維修”條件下，部件的狀態不僅取決于其本身的劣化規律，同時需要考慮維修效果的變化規律，在這種條件下，采用解析方法進行維修決策優化建模的難度大大增加，而仿真建模方法由于能夠避免復雜的解析運算，適于描述“不完全維修”條件下多部件系統的狀態劣化過程，因此逐漸受到了研究者的關注。

對于多部件系統來說，其狀態維修決策優化不僅需要考慮部件的狀態劣化規律，同時需要對部件之間的相關性進行分析，以精確衡量故障風險與狀態維修效益，進行優化決策。Wang等[3]采用仿真方法描述狀態隨機劣化過程，提出了維修行為決策閾值以及檢測間隔期的序貫優化決策算法。Marseguerra等[4]采用仿真方法建立了系統狀態劣化過程模型，建立了以費用最小化為目標的狀態維修決策優化模型。Berenguer等[5]采用仿真方法建立了兩部件系統狀態劣化模型，對經濟相關性條件下多部件系統的維修決策優化方法進行了研究。上述研究都對“不完全維修”的效果進行了確定性假設，一定程度上降低了建模難度，但事實上“不完全維修”的耗時、效果等會不可避免地存在一定的隨機性，在建模過程中考慮此類因素將有助于提高建模精度，增強維修決策的科學性。為了更真實地描述故障和維修過程，本文采用仿真方法，對“不完全維修”條件下的多部件系統狀態維修優化方法進行研究。

1 多部件系統狀態劣化過程模型

假定多部件系統內，各部件僅存在經濟相關性，即系統內各部件的狀態劣化過程是獨立的。那么從決策者的角度看，一方面要從部件的角度獨立地權衡系統預防維修的成本與收益，同時應考量各部件組合維修的可能性，蒙特卡洛仿真方法能夠有效地描述這種包含復雜的狀態劣化與維修的隨機過程[6-8]。

本文在“不完全維修”條件下，以多部件系統內單一部件狀態維修閾值為決策變量，進行狀態維修決策優化研究。因此，在有限周期內，以單位壽命費用最小為目標，對多部件系統內各部件的預防性維修閾值進行優化決策，以達到提高狀態維修效益的目的。

1.1 多部件系統狀態隨機劣化過程

對于存在經濟相關性的多部件系統，在不考慮維修的條件下，系統內各部件的狀態劣化過程是隨機且獨立的。假設多部件系統內包含N個部件，且各部件的狀態劣化過程都滿足以下條件：

1)部件i(i=1,2,…,N)狀態指標di(t)的值域是連續的；

2)部件i(i=1,2,…,N)狀態指標di(t)被連續監測，監測時間和費用忽略不計；

6)部件i(i=1,2,…,N)隨機失效，一旦發生失效則立即進行事后更換；

7)部件i(i=1,2,…,N)狀態劣化以及失效相互獨立，任一部件停機都將導致系統停機。

目前，研究者多采用gamma過程來描述部件狀態劣化規律[9-12]，gamma過程假定系統的壽命過程是一個勻速狀態劣化過程，實際上，疲勞裂紋等失效模式往往隨時間呈現加速劣化趨勢，gamma過程不適于描述此類劣化過程，因此需要建立適用的模型來描述此類狀態劣化過程。對于傳動軸、軸承等部件，疲勞裂紋等是導致其失效的主要故障模式，表征這類故障模式的狀態指標通常不滿足馬氏性，對于系統內部件i，其未來狀態與其當前狀態直接相關，有

di(t)=(1+ξi)di(t-1)，ξ≥0，

(1)

式中:di(t)為部件i在t時刻的狀態值；ξ為狀態相對劣化速率；ξi為非負隨機數。

由(1)式可知，di(t)是一個非減的隨機劣化過程，圖1所示為采用蒙特卡洛方法得到的di(t)隨機劣化仿真結果。由圖1可知部件i具有較明顯的耗損期，適于采用狀態維修策略。

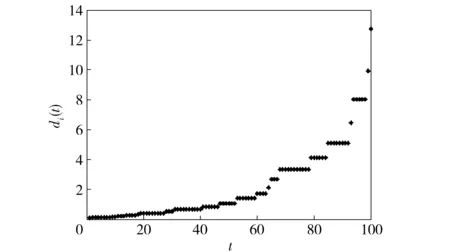
圖1 某部件的狀態隨機劣化過程Fig.1 Stochastic deteriorating process of a certain component

由于部件i在壽命周期內隨機失效，因此隨著仿真時間的推進，將時變的失效概率值與(0，1)分布的隨機數進行序貫判別。隨著di(t)的劣化，失效概率值相應增大，若未失效，表示狀態正常，繼續仿真；否則對裝備進行事后更換。由于冪指數函數能夠反映常見狀態指標與故障風險之間的非線性映射關系，因此這里采用冪指數函數來構造失效概率函數Fi(x)：

(2)

圖2所示為某部件失效概率函數，其中a=0.4，b=2.

圖2 裝備失效概率函數Fig.2 Failure reliability function of equipment

1.2 部件的不完全維修

根據裝備維修實際可知，預防性維修通常無法將部件狀態恢復到初始狀態，而且維修效果往往受資源投入量、累計維修次數等因素的影響，因此假設：

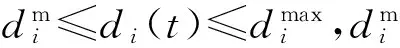
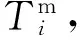
(3)

(4)

假設某部件dm=16，μm=0.5和σm=0.5，則該部件預防性維修后狀態概率分布函數如圖3所示。

圖3 預防性維修后狀態概率分布函數(dm=16, μm=0.5，σm=0.5)Fig.3 Probability distribution function of equipment after preventive maintenance (dm=16, μm=0.5，σm=0.5)

由圖3可知，預防性維修能夠以96.19%的概率使裝備修后狀態保持在4以下。

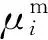
(5)

圖4所示為隨預防性維修次數變化的修后狀態概率密度分布曲線的示意圖。

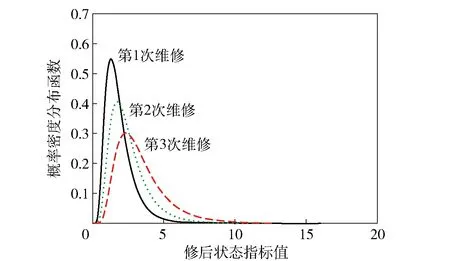
圖4 隨維修次數變化的修后狀態概率密度分布函數Fig.4 Probability density function of condition determined by preventive maintenance times ( μmi，1=0.5，σm =0.5，ω=0.2)

如圖4所示，隨著預防性維修次數的累積，裝備修后狀態接近初始狀態的概率將降低。

(6)

(7)

(8)

1.3 壽命周期維修費用

當預防性維修、預防性更換和事后更換所需的費用和時間依次遞增時，預防性維修決策才是可行的，因此根據這一前提，對上述3類費用的組成成分進行劃分。預防性維修的費用包括3個部分：資源費用、工時費用以及調試費用。其中，資源費用是指維修設備、器材、備件等的費用，資源費用越高部件維修效果通常也越好；工時費用是指維修人員的費用，維修所需時間越長，工時費用就越高；第3部分為調試費用，為了保證修后部件狀態良好，需要進行狀態調試，因此任何預防性維修和預防性更換都將產生調試費用。

任何故障或維修行為導致的停機，都將對系統的使用可用度造成不利影響，為了度量停機所造成的損失，在壽命周期費用中引入了停機損失費用。

多部件系統壽命周期費用的內容和定義為：

5)調試費用Cpms，在多部件系統內發生任意的預防性維修行為，都將產生調試費用Cpms，Cpms為定值，表示調試費用不受系統內被修部件的數量影響；

6)單位停機時間損失費用Cd，任何維修行為都將對系統可用度產生不利影響，Cd能夠在決策目標中表示決策者對可用度的偏好程度。

2 預防性維修閾值仿真優化

2.1 狀態隨機劣化算法

(9)

式中：λi(λi>0)為常數；uU[0，1]；φi(0<φi<1)為常數。

由(9)式可知，狀態指標保持不變的概率為φi，而λi即為ξi的最大取值。

2.2 裝備狀態隨機劣化過程仿真

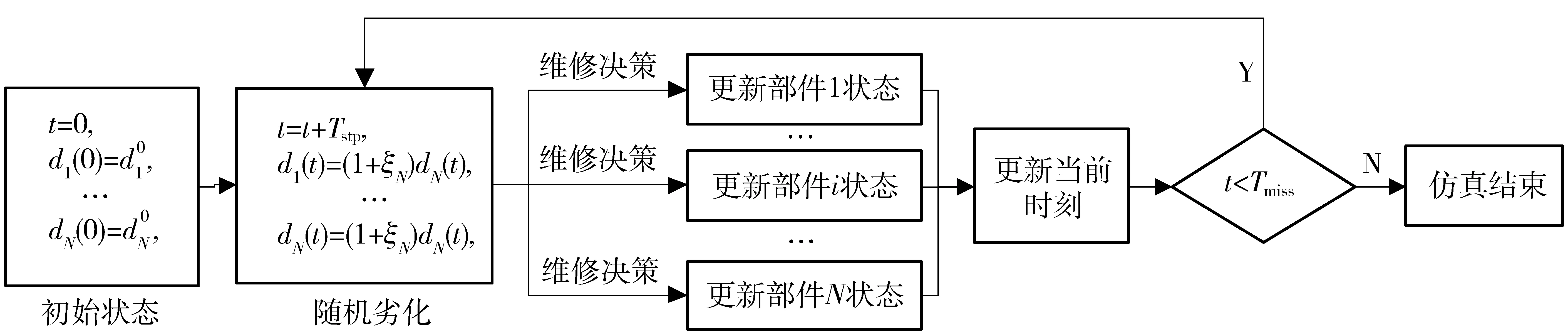
圖5 部件狀態隨機劣化仿真過程Fig.5 Simulation of stochastic deteriorating process of components

圖5中，在每個仿真時刻，各部件狀態的隨機劣化是相互獨立的過程，仿真模型以部件狀態為依據進行維修決策，實施維修和更新各部件的狀態。部件維修耗時獨立計算。在更新當前時刻后，對仿真結束條件進行判別，若達到預定周期，則結束仿真并輸出結果，否則繼續仿真。

在仿真過程中，不同的維修行為將產生不同的費用，仿真程序在更新系統內部件狀態的同時更新相應的維修費用。根據1.3節提出的關于費用假設，單步仿真費用計算流程如圖6所示。

圖6 單步仿真費用Fig.6 Expenses within one simulation step

在圖6中，在單步仿真過程中，首先依據部件狀態分別計算各部件的維修費用，然后對部件維修進行或運算，確定系統內是否有預防性維修，計算系統級費用。

2.3 狀態維修決策閾值優化流程

圖7所示為預防性維修閾值的優化流程，根據決策者對費用的敏感程度，可以通過設定費用優化精度確定尋優終止條件，當最優與次最優費用差滿足精度要求時，即可結束尋優，輸出預防性維修閾值的最優值。

圖7 預防性維修閾值的優化流程Fig.7 Optimization process of preventive maintenance threshold

3 案例分析

表1所示為部件1狀態劣化過程的相關參數。表2所示為部件1的維修決策費用參數。

表1 部件1狀態劣化過程相關參數Tab.1 Parameters related to the deteriorating process of condition

表2 部件1維修決策費用參數Tab.2 Expenditure parameters for maintenance decision-making of Part 1

為了便于分析，假定部件2與部件1其他參數相同，只有隨機劣化概率φ和費用參數存在差別。表3所示為部件2與部件1存在差異的參數。

表3 部件2與部件1存在差異的參數Tab.3 Parameters of Part 2 and Part 1

由表3可知，與部件1相比，部件2的劣化速度更慢，但預防性維修、預防性更換和事后更換費用等都相對更高。

圖8 兩部件系統的單位時間費用等高曲線(S=1)Fig.8 Average cost contour plot of system with two components(S=1)

圖9 兩部件系統的平均費用等高曲線(S=0.5)Fig.9 Average cost contour plot of system with two components(S=0.5)

表4 兩部件系統的平均費用Tab.4 Average expenditure of system with two components

在仿真過程中，按照維修類型統計兩部件的費用構成，得到的數據如表5所示。

表5 兩部件系統的費用構成Tab.5 Detailed expenditure composition of system with two components

由表5可知，兩部件系統在多次仿真過程中都未實施預防性更換，表明從費用角度看，預防性維修的經濟效益要明顯好于預防性更換。同時，雖然部件2的劣化速度相對較慢，但由于該部件事后更換費用更高，因此部件2的預防性維修閾值相對更小，導致該部件在系統總費用中所占比重反而較小。

為了驗證本文提出方法的有效性，在不考慮預防性維修的條件下，對兩部件系統的狀態劣化過程進行仿真，得到的仿真結果表6所示。

如表6所示，采用本文優化得到的預防性維修閾值進行維修，可以將更換周期平均費用從221.670 7降低到141.641 2，降幅高達36.10%，同時可以將壽命周期內的裝備可用度從無預防性維修條件下的91.57%提高到95.81%，系統失效停機次數從2.172 1降低到了0.659 5. 因此，從經濟性、任務性和安全性的相關指標看，本文提出的預防性維修閾值優化方法都是適用且有效的。

表6 不同維修策略下兩部件系統仿真結果Tab.6 Simulated results system with two components given different maintenance strategies

4 結論

狀態維修對提高裝備戰備完好性、降低壽命周期費用，防止重大事故發生起著重要的作用。對于復雜的多部件裝備系統來說，從整體費用的角度出發對部件預防維修閾值進行優化，將有助于控制系統的整體風險，使決策對整體系統來說達到最優。

本文在建立部件狀態劣化過程模型的基礎上，將有限周期內，部件“不完全維修”效果與維修次數之間的關系進行了顯示的函數表達，有利于更真實地表示和評價預防性維修行為對部件以及系統的影響。

采用蒙特卡洛仿真方法建立的多部件系統整體劣化模型能夠較好地反映系統內部件的獨立劣化過程以及“不完全維修”的隨機性，有效地避免了解析求解容易引起的維度爆炸問題。案例分析結果也表明，在有限周期內單位壽命費用最小的決策優化目標下，采用仿真方法確定的最優預防性維修閾值是適用且有效的。

References)

[1] Bengtsson M. Condition based maintenance system technology-where is development heading?[C]∥17th European Maintenance Congress. Barcelona, Spain: Euro Maintenance, 2004:580-588.

[2] 張小麗, 陳雪峰, 李兵, 等. 機械重大裝備壽命預測綜述[J].機械工程學報, 2011, 47(11):100-116. ZHANG Xiao-li, CHEN Xue-feng, LI Bing,et al.Review on life prediction of major mechanized equipment[J]. Journal of Mechanical Engineering, 2011, 47(11):100-116.(in Chinese)

[3] Wang W. Modeling condition monitoring intervals: a hybrid of simulation and analytical approaches[J]. Journal of the Operational Research Society, 2003, 54(3):273-282.

[4] Marseguerra M, Zio E. Optimizing maintenance and repair polices via a combination of generic algorithms and Monte Carlo simulation[J]. Reliability Engineering & System Safety, 2000, 68(1): 69-83.

[5] Bérenguer C, Grall A, Castanier B. Simulation and evaluation of condition-based maintenance polices for multi-component continuous-state deteriorating system[C]∥Foresight and Precaution: Proceedings of ESREL 2000, SARS and SRA-Europe Annual Conference. Amsterdam, Dutch:August Aimé Balkema, 2000:275-282.

[6] Doostparast M, Kolahan F, Doostparast M. A reliability-based approach to optimize preventive maintenance scheduling for coherent systems[J]. Reliability Engineering & System Safety. 2014, 126: 98-106.

[7] Hai C V, Do P, Barros A. Maintenance grouping strategy for multi-component systems with dynamic contexts[J]. Reliability Engineering & System Safety, 2014, 132:233-249.

[8] Zhu W J, Fouladirad M, Bérenguerc C. A multi-level maintenance policy for a multi-component and multifailure mode system with two independent failure modes[J]. Reliability Engineering & System Safety, 2016,153: 50-63.

[9] Barker C T, Newby M J. Optimal non-periodic inspection for a multivariate degradation model[J]. Reliability Engineering & System Safety, 2009(1):33-43.

[10] Amari S V, Mclaughlin L. Optimal design of a condition-based maintenance model[C]∥Annual Reliability and Maintainability Symposium. Los Angeles, CA, US:IEEE, 2004:528-533.

[11] Wang W, Majid H B A. Reliability data analysis and modeling of offshore oil platform plant[J]. Journal of Quality in Maintenance Engineering, 2000, 6(4):287-295.

[12] Ghasemi A, Yacout S, Ouali M S. Optimal condition based maintenance with imperfect information and the proportional hazard model[J]. International Journal of Production Research, 2007, 45(4): 989-1012.

Optimal Condition-based Maintenance Decision-making Method of Multi-component System Based on Simulation

WANG Shao-hua1, ZHANG Yao-hui1, XU Long-yang1, LIU Hong-xiang2

(1.Department of Technology Support Engineering, Academy of Armored Force Engineering, Beijing 100072, China; 2.Department of Science Research, Academy of Armored Force Engineering, Beijing 100072, China)

To promote the maintenance benefit by combined maintenance, for multi-component systems subjected to condition-based maintenance each component is supposed to endure independent gradual deterioration, and a stochastic deteriorate model is established. The exponential function is applied to set up the reliability functions taking condition parameters as variables. In consideration of imperfect maintenance and probability distribution of maintenance time, a Monte Carlo-based condition deteriorating simulation model of multi-component system is proposed. TA preventive maintenance threshold optimization model is constructed by taking the expected expenses per unit time as the optimization objective, and is verified by a case study.

ordnance science and technology; condition-based maintenance； imperfect maintenance； Monte Carlo simulation； optimal decision-making

2016-05-13

軍隊科研計劃項目(51327020303)

王少華(1986—)，男，講師，博士。E-mail:aafe77330@163.com

E92

A

1000-1093(2017)03-0568-08

10.3969/j.issn.1000-1093.2017.03.021